Hartree fock theory

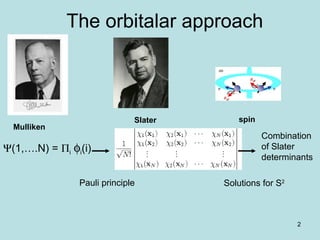
2
The orbitalar approach
Mulliken
Ψ(1,….N) = Πi φi(i)
Slater
Combination
of Slater
determinants
Pauli principle Solutions for S2
spin

3
MO approach
A MO is a wavefunction associated with a
single electron. The use of the term "orbital"
was first used by Mulliken in 1925.
Robert Sanderson
Mulliken
1996-1986
Nobel 1966
We are looking for wavefunctions for a
system that contains several particules. We
assume that H can be written as a sum of
one-particle Hi operator acting on one
particle each.
H = Σi Hi Ψ(1,….N) = Πi φi(i)
E = Σi Ei

4
MO approach
MO theory was developed, in the years after valence bond
theory (1927) had been established, primarily through the
efforts of Friedrich Hund, Robert Mulliken, John C. Slater,
and John Lennard-Jones. The word orbital was introduced
by Mulliken in 1932. According to Hückel, the first
quantitative use of MO theory was the 1929 paper of
Lennard-Jones. The first accurate calculation of a molecular
orbital wavefunction was that made by Charles Coulson in
1938 on the hydrogen molecule. By 1950, MO were
completely defined as eigenfunctions of the self-consistent
field
Friedrich Hund
1896-1997
Charles Alfred Coulson
1910-1974

5
Generalizing the
LCAO approach:
A linear combination of
atomic orbitals or LCAO
It was introduced in 1929 by Lennard-Jones
with the description of bonding in the
diatomic molecules of the first main row of
the periodic table, but had been used earlier
by Pauling for H2
+
.
Sir John Lennard-Jones
1894-1954
Linus Carl Pauling
1901-1994 Nobel 1962

6
Schrödinger equation for LCAO
Erwin Rudolf
Josef Alexander
Schrödinger
Austrian
1887 –1961
HΨ = EΨ
This is the set of linear equation solved for
| Hij-E S ij |= 0 Secular determinant
In an ab-initio calculation, all the Hij and Sij
Integrals are rigorously calculated.
To do that, one need defining a set of AOs
(basis set) and the geometry.
There is no parameterization.
A subjective choice concerns that the basis
set (always incomplete). The best calculation
(SCF level or after IC) is that providing the

7
Particles are
electrons
Born-Oppenheimer
approximation
1927
Max Born German
(1882-1970)
Julius Robert Oppenheimer
Berkeley- Los alamos
1904 –1967
HH = [Te +VN-e + Vee] + TN + VN-N
HHee = [Te +VN-e + Vee]
Ψ = ΠΨ(e) ΠΨ(Ν)
e N
VN-e also acts on N; when N is
considered as fixed: VN-e then
becomes an operator acting on e.
Separation of Ψ(e) and Ψ(N)
Should be a
coupling term
}Operator acting on e

8
Born-Oppenheimer
approximation
The forces on both electrons and nuclei due to
their electric charge are of the same order of
magnitude; since the nuclei are so much more
massive than the electrons, they must
accordingly have much smaller velocities.
. Nucleon mass / Electron mass = 1835
For the same kinetic energy, when an electron travels meter a
nucleus of hydrogen travels 2.3 cm, that of carbon 6.7
millimeters and that of gold 1.7 millimeters. It is then
considered as the movement of nuclei and electrons are
independent, that electrons adapt instantaneously to the
movement of nuclei. It is said that the electrons follow
adiabatically the motion of the nuclei.

9
A physical system remains in its
instantaneous eigenstate if a given
perturbation is acting on it slowly
enough and if there is a gap
between the eigenvalue and the
rest of the Hamiltonian's spectrum.
The adiabatic theorem 1928
Max Born German
(1882-1970)
Vladimir
Aleksandrovich
Fock russian
1898–1974
This adiabatic principle is crucial because it allows
us to separate the nuclear and electronic motion,
leaving a residual electron-phonon interaction.
From this point on it is assumed that the electrons
respond instantaneously to the nuclear motion and
always occupy the ground-state of that nuclear
configuration.

10
Vibrations, nuclear motion
Developing U around the equilibrium position (r = req)
gives U(∆r) = U° + U’’(req)∆req
2
: The angular frequency is
ω = (req/m) ½
depending on the reduced mass m=m1m2(m1+m2)
3N-6 degree of freedom + 3 translations and 3 rotations for the general case.

11
These are surfaces that can be achieved step by step from
calculations developed. They may be significant changes in the
characters of orbital obtained. According to an internuclear
distance ionic or covalent change significantly.
In the case of rapidly changing systems (collision dissociations
from excited states), the nature of the orbital can not change and
the Born-Oppenheimer approximation is no longer valid. The state
surface is therefore a surface potential where the same dominant
character is always found. Such surface, called diabatic surface,
is in some region the ground state and for some region an excited
state. Then, there is a jump from an adiabatic surface to another!
The diabatic surfaces are inherently difficult to obtain since
calculations lead to the system that is most stable.
The surface energy obtained
under the Born-Oppenheimer
approximation: adiabatic
surfaces.

12
Covalent
Ionic
An ionic curve “naturally” correlates with ions whereas a
covalent one dissociates to generate radicals. This leads to an
avoided crossing.
PES: Potential Energy Surfaces.
dNa-Cl
U(d)
Na+
+ Cl-
Na + ClAdiabatic
Diabatic
Diabatic

13
The diabatic surface should in principle be obtained by
calculating the coupling terms <φ1|TN|φ2> allowing possible
jumps from one adiabatic surface to another.
This is uneasy since the basis set gives an avoided crossing
without the coupling. The usual procedure is generally the
reverse: impose “natural orbitals” and minimize the coupling
terms to allow the surfaces crossing.
Finding diabatic surfaces

14
Diabatic- Adiabatic surfaces.
adiabatic diabatic
Process velocity slow fast
Born-Oppenheimer valid Not valid
electrons
adaptation to the
nuclei motion
Adapt
(follow it)
Do not
(delay to
follow nuclei)
Natural MO
character
May switch Remains
constant

15
Approximation of
independent particles
HHartree
= Σi Fi
The hamiltonian, HHartree
, is the sum of Fock operators
only operating on a single electron i.
The wave function is the determinant of orbitals, φ(i) to
satisfy the Pauli principle. Fi φ(i)=εi φ(i)
EHartree
= Σi εi
Douglas Rayner
Hartree English
1897 1958
Vladimir
Aleksandrovich
Fock russian
1898–1974
1930

16
Approximation of
independent particles
Fi = Ti + Σk Zik/dik+ Σj Rij
Each one electron operator is the sum of one
electron terms + bielectronic repulsions
Hartree Fock
Rij is the average repulsion of the electron j upon i.
The self consistency consists in iterating up to
convergence to find agreement between the postulated
repulsion and that calculated from the electron density.
This ignores the real position of j vs. i at any given time.
1927

17
Self-consistency
Given a set of orbitals Ψ°i, we calculate the
electronic distribution of j and its repulsion
with i.
This allows expressing
and solving the equation to find new Ψ1
i
allowing to recalculate Rij. The process is
iterated up to convergence. Since we get
closer to a real solution, the energy
decreases.
Fi = Ti + Σk Zik/dik+ Σj Rij

18
Jij, Coulombic integral for 2 e
Let consider 2 electrons, one in orbital Ψ1, the other in orbital Ψ2, and
calculate the repulsion <1/r12>.
Assuming Ψ= Ψ1Ψ2
This may be written
Dirac notation used in physics
Notation for
Assuming Ψ= Ψ1Ψ2

19
Jij, Coulombic integral for 2 e
Jij = < Ψ1Ψ2IΨ1Ψ2> = (Ψ1Ψ1IΨ2Ψ2) means the product of two
electronic density ↔ Coulombic integral.
This integral is positive (it is a repulsion). It is large when dij
is small.
When Ψ1 are developed on atomic orbitals φ1, bilectronic
integrals appear involving 4 AOs (pqIrs)
Assuming Ψ= Ψ1Ψ2

20
Jij, Coulombic integral involved in
two electron pairs
electron 1: Ψ1 or Ψ1 interacting with electron 2: Ψ2 or Ψ2
When electrons 1 have different spins (or electrons 2 have different
spins) the integral = 0. <αΙβ>=δij. Only 4 terms are ≠ 0 and equal to Jij.
The total repulsion between two electron pairs is equal to 4Jij.
Assuming Ψ= Ψ1Ψ2

21
Particles are electrons!
Pauli Principle
electrons are indistinguishable:
|Ψ(1,2,...)|2
does not depend on
the ordering of particles
1,2...:
| Ψ (1,2,...)|2
= | Ψ (2,1,...)|2
Wolfgang Ernst Pauli
Austrian 1900 1950
The Pauli principle states that electrons are fermions.
Thus either Ψ (1,2,...)= Ψ (2,1,...) S bosons
or Ψ (1,2,...)= -Ψ (2,1,...) A fermions

22
The antisymmetric function is:
ΨA = Ψ (1,2,3,...)-Ψ (2,1,3...)-Ψ (3,2,1,...)+Ψ (2,3,1,...)+...
which is the determinant
Particles are fermions!
Pauli Principle
Such expression does not allow two electrons to be in the same state
the determinant is nil when two lines (or columns) are equal;
"No two electrons can have the same set of quantum numbers".
One electron per spinorbital; two electrons per orbital.
“Exclusion principle”

23
The simplest way to approximate the wave function of a many-particle
system is to take the product of properly chosen wave functions of the
individual particles. For the two-particle case, we have
This expression is a Hartree product. This function is not antisymmetric.
An antisymmetric wave function can be mathematically described as
follows:
Therefore the Hartree product does not satisfy the Pauli principle. This
problem can be overcome by taking a linear combination of both Hartree
products
where the coefficient is the normalization factor. This wave function
is antisymmetric and no longer distinguishes between fermions.
Moreover, it also goes to zero if any two wave functions or two
fermions are the same. This is equivalent to satisfying the Pauli
exclusion principle.
Two-particle case

24
.
The expression can be generalized to any number of fermions by writing it as a
determinant.
Generalization: Slater determinant
John Clarke Slater
1900-1976

25
Kij, Exchange integral for 2 e
Let consider 2 electrons, one in orbital Ψ1, the other in orbital Ψ2, and
calculate the repulsion <1/r12>.
Assuming Ψ= 1/√2 IΨ1Ψ2I
Kij is a direct consequence of the Pauli principle
Dirac notation used in physics
Notation for
Obeying Pauli principleΨ= 1/√2 IΨ1Ψ2I Slater determinant

26
It is also a positive integral (-K12 is negative and corresponds to a
decrease of repulsion overestimated when exchange is ignored).
Kij, Exchange integral
two electron pairs

27
Interactions of 2 electrons

28
Jij-Kij
Unpaired electrons: σgσu
Singlet and triplet states
bielectronic terms
Kij
Jij
│ΨiΨj│ │ΨiΨj│
│ΨiΨj│ │ΨiΨj│
│ΨiΨj│- │ΨiΨj│
│ΨiΨj│+ │ΨiΨj│Jij+Kij

29
Jj and Kj operators
We need to express the ij bielectronic repulsion as one electron
operator Rj acting on Ψj and representing the repulsion with an
average distribution of j.
Rj is the sum of 2 operators Jj and Kj.

30
Slater rules
Hartree-Fock Operators are 1 or 2 electron operators ( i or ij).
Developing the polyelectronic wavefunction leads only to the
following contributions
<χ1Iχ1> <χ2Iχ2> ….. <χiIOIχi> ….. <χNIχN>
or <χ1Iχ1> <χ2Iχ2> ….. <χiχjIOIχiχj> ….. <χNIχN>
Only the terms <χ1Iχ1>=1 remain, the others being nil: <χ1Iχ≠1>=0

31
Slater rules
Non zero terms arise from 3 possibilities:
• Dl = DR <DlIOIDR> = Σ [<kikjIOIlilj> - <kikjIOIlilj>]
• Dl differ from DR by one orbital i
<DlIOIDR> = <kiIOIlj>
<DlIOIDR> = Σ [<kikjIOIlilj> - <kikjIOIlilj>]
• Dl differ from DR by two orbitals i and j
<DlIOIDR> = <kikjIOIlilj> - <kikjIOIlilj>
i<j
N
i≠
j
N

32
Electronic energy
i is the index for an orbital:
EE = Σεi εi = <φiIhIφi>+ Σ (2Jij-Kij)
occocc
j
Each i electron interacts with 2 j
electrons with opposite spins Jij-Kij with
that of the same spin for and Jij for that
with different spin.

33
Electronic energy – total energy
The sum of the energies of all the electrons
contains the ij repulsion twice:
EE = Σεi εi = <φiIhIφi>+ Σ (2Jij-Kij)
occocc
i
EE = Σ[hii + Σ repij
occ
ji
occ
= Σ [hii+2 Σ Repij
j
occ occ
] ]
ESCF = <ΨSCFIHIΨSCF> = Σhii + Σ Σ(2Jij-Kij)
j<ii
occ occ
ESCF +ENETOTAL =
ESCF is defined as the energy of ΨSCF applying Slater rules
ESCF = EE - Repij = Σhii + Repij
i
i
occPauli principle
occ
i

34
Restricted Hartree-Fock
Closed-shell system: an MO is doubly occupied or
vacant. The spatial functions are independent from the
spin. Assuming k and l with spin α, the expression of
a Fock matrix-element, Fkl, is
Fkl = h + 2J – K and
εi = hii + Σ (2Jij-Kij)
ESCF = 2Σ εi – ΣΣ(2Jij-Kij)
occ occ
J of spin α J of spin β
Fkl = hkl + Σ [(klIjj)-(klIjj)] - Σ (klIjj)
occ
j
occ occ occ
i j<ii
There is no exchange
term for electrons with
different spin (<αΙβ>=0)
Altogether there are 2 J
for one K.

35
Restricted Hartree-Fock
Why the HOMO-LUMO electron gap is overestimated?
For a virtual i orbital the repulsion
concerns all the electrons
i
i
For an occupied i orbital the repulsion
concerns all the electrons minus 1
(itself)
The repulsion is larger for an unoccupied level than for
an occupied one!
occ
j

36
Koopmans theorem
εi = - IP
Tjalling C.
Koopmans
Dutch
Nobel Prize in
Economic
Sciences
in 1975
occ
j
(Physica, 1, 104 (1933)
This theorem applies for a “vertical transition”:
sudden without time for electronic reorganization.
The orbitals do not relax!
This theorem is obvious for Hückel-type approaches:
The AOs are fixed. The total energy is the sum of the
orbital energies:
IP = 2Σ εj -
j occ≠i
2Σ εj
j
j occ
j
This theorem is obvious for Hückel-type approaches:
The AOs are fixed. The total energy is the sum of the
orbital energies:
It is less obvious in HF since ESCF≠ Σ εi
= 2Σ εj -
j occ≠i
2Σ εj
j occ≠i
j
- εi
For DFT, the Janak theorem is a generalization of Koopman’s theorem. J. F. Janak, Phys. Rev.
B 18, 7165; J.P. Perdew, R. G. Parr, M. Levy et J. L. Balduz Jr., Phys. Rev. Lett. 23 (1982) 1691.

37
Koopmans theorem
εk = - IP
Tjalling C.
Koopmans

38
What is wrong with Koopmans
theorem?
The AOs are not “fixed” but relax (“breath”); the Slater exponents
depend on the bielectronic repulsion. The subtraction in the previous
slide suppose no variation. The relaxation is important for polarisable
systems (metals, the work function is generally weak).
Calculating with AOs for the neutral species underestimates the
energy for the ionized species. IP is overestimated by Koopmans
theorem.
How to proceed more rigorously?
Calculate the IP as the difference of the total energy for two states.

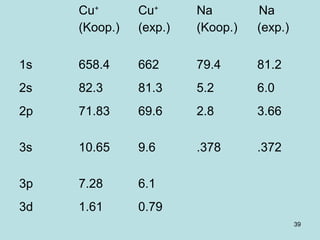
39
Cu+
(Koop.)
Cu+
(exp.)
Na
(Koop.)
Na
(exp.)
1s 658.4 662 79.4 81.2
2s 82.3 81.3 5.2 6.0
2p 71.83 69.6 2.8 3.66
3s 10.65 9.6 .378 .372
3p 7.28 6.1
3d 1.61 0.79

40
Open-Shell – spin contamination
Let assume that here is one α electron more than β.
For them Fock matrix elements, there is one more exchange term for the
α electrons than for the β’s. The matrix elements are not the same and
solving the secular determinants for α and β independently leads to
different solutions.
φi ≠ φi .
The UHF (unrestricted Hartree-Fock method) solves
the secular equation for α and β independently and
obtains different spatial functions for α and β.
This does not allow to have eigenfunctions of the spin
operators.
i
j
i
k
k
j

41
ROHF
The same spatial function is taken whatever the
spin is.
Robert K. Nesbet
This allows eigenfunctions of spin operators.
This allows separating spatial and spin functions.
It is not consistent with variational principle (that
does better without this constraint).
F = h + Σ [( Ijj)-( jI j)] - Σ ( Ijj)-1/2 ( jI j)
2e occ 1e occ
j j

42
Spin operator
The spinorbitals should be solution of SZ and
S2
. This is not the case for UHF.

43
Niels Henrik David Bohr
Danish
1885-1962
Correspondence principle 1913/1920
For every physical quantity
one can define an
operator. The definition
uses formulae from
classical physics replacing
quantities involved by the
corresponding operators
Classical expression Quantum expression
lZ= xpy-ypx
For an angular momentum

44
In quantum mechanics angular momentum is defined by an operator
where r and p are the position and momentum operators respectively. In
particular, for a single particle with no electric charge and no spin, the angular
momentum operator can be written in the position basis as
This orbital angular momentum operator is the most commonly encountered
form of the angular momentum operator, though not the only one. It satisfies
the following canonical commutation relations:
,
It follows, for example,
Angular momentum

45
L2
is the norm and Lx, Ly, Lz are the projections.
[Jx, Jy]= i Jz [Jx, J2
]= 0
[Jy, Jz]= i Jx eigenfunctions of J2
are j(j+1)
[Jz, Jx]= i Jy eigenfunctions of Jz are m
J2
Ij,m> = j(j+1) Ij,m> and Jz Ij,m> = m Ij,m>
Relations in Angular momentum
In atomic units, h =1

47
spin
• For an electron: s =1/2 → S2
=s (s +1) =3/4
and ms=±1/2.
• A spin vector is either α |s,ms> = |1/2,1/2> or
β: |s,ms> = |1/2,-1/2>

48
spin
For several electrons: the total spin is the vector sum of the
individual spins.
• For the projection Sz=Ms = Σs ms
• For the norm S2
= S1
2
+S2
2
+2S1S2
S2
=[S1z
2
+S1z+S1-S1+]+[S2z
2
+S2z+S2-S2+]+[(S1+S2- ++S1-S2+)+2S1zS2z]
• For 2 electrons, there are 4 spin functions:
α(1) α(2), β(1) β(2), α(1) β(2) and α(2) β(1) that are
solutions of Sz.
Are they solution of S2
?

49
α(1)α(2) is solution of S2
α(1) (Sz
2
+Sz+S-S+) α(2) [1/2]2
+ 1/2 + 0 0.75
α(2) (Sz
2
+Sz+S-S+) α(1) [1/2]2
+ 1/2 + 0 0.75
2Szα(1)Szα(2) 2 ½ ½ 0.5
S-α(1)S+α(2) 0 0
S+α(1)S-α(2) 0 0
total 2
S2
α(1) α(2) = 2 α(1) α(2)

50
α(1)β(2) is not a solution of S2
α(1) (Sz
2
+Sz+S-S+) β(2) [1/2]2
- 1/2 + 1 0.75
β(2) (Sz
2
+Sz+S-S+) α(1) [1/2]2
+ 1/2 + 0 0.75
2Szα(1)Szβ(2) 2 ½ (-½) -.5
S-α(1)S+β(2) β(1) α(2) β(1) α(2)
S+α(1)S-β(2) 0 0
total 2
S2
α(1) β(2) = α(1) β(2) + β(1) α(2)

51
α(1)β(2)± β (1) α (2) are solutions of S2
S2
α(1) β(2) = α(1) β(2) + β(1) α(2)
S2
β(1) α(2) = β(1) α(2) + α(1) β(2)
S2
(α(1) β(2) + β(1) α(2)) = 2 (α(1) β(2) + β(1) α(2))
S2
(α(1) β(2) − β(1) α(2)) = 0 (α(1) β(2) − β(1) α(2))
The spinorbitals must then be a product of such expressions by a
constant (a spatial term which is a constant for the spin operator).
We should be able to separate the spatial and the spin contributions.

52
Use of indentation operators
upon vector sums
S2
=Sz
2
+Sz+S-S+
S-S+ |1,1> = 0
S-S+ |1,0> = (1+0+1)(1-0) |1,0> = 2|1,0>
S-S+ |1,-1> = (1-1+1)(1+1) |1,-1> = 2 |1,-1>
Singlet S2
|0,0> = [0+0+0] =0 |0,0>
Triplet S2
|1,1> = [1+1+0] |1,1>
Triplet S2
|1,0> = [0+0+2] |1,0>
Triplet S2
|1,-1> = [1-1+2] |1,-1>

53
S2
as an operator on determinant
S2
(D)= Pαβ(D) + [(nα-nβ)2
+2nα +2nβ ] D
Pαβ is an operator exchanging the spins :α ↔ β
nα and nβ are the # of electrons of each spin
Application:
S2
(IaaI) = IaaI+IaaI = -IaaI+IaaI = 0
S2
(IabI) = IabI+IabI
S2
(IabI-IbaI) = 2 (IabI+IabI)= 2 (IabI-IbaI)
S2
(IabI+IbaI) = IabI+IbaI+IabI+IbaI
= -IbaI-IabI+IabI+IabI = 0

54
A single Slater determinant is not
necessarily an eigenfunction of S2
Separation of spatial and spin functions
IabI= a(1)α(1) b(2)β(2) - b(1)β(1) a(2)α(2)
= a(1)b(2) α(1)β(2) - b(1)a(2) α(2)β(1)
is not a eigenfunction of S2
if a≠b

55
A combination of Slater
determinant then may be an
eigenfunction of S2
The separation of spatial and spin functions is possible
If the spatial function (a or b) is associated with opposite spins
IabI± IbaI = a(1)b(2) α(1)β(2) - b(1)a(2) α(2)β(1)
are a eigenfunction of S2
± b(1)a(2) α(1)β(2) - a(1)b(2) α(2)β(1)
[a(1)b(2) + b(1)a(2)] (α(1)β(2) - α(2)β(1))IabI+ IbaI =
+
[a(1)b(2) - b(1)a(2)] (α(1)β(2) + α(2)β(1))IabI- IbaI =

56
UHF: Variational solutions are not
eigenfunctions of S2
The separation of spatial and spin functions is not possible
If 2 spatial functions (a ≠ a’; b ≠ b’) are associated with
opposite spins
Iab’I+ Iba’I = a(1)b’(2) α(1)β(2) - b’ (1)a (2) α(2)β(1)
+ b(1)a’(2) α(1)β(2) – a’(1)b(2) α(2)β(1)
=[a(1)b’(2) + b(1)a’(2)](α(1)β(2) - [a’(1)b(2) + b’(1)a(2)] α(2)β(1))
Not equal

Hartree fock theory

More Related Content

What's hot

Similar to Hartree fock theory

More from استاذ الفيزياء النووية

Recently uploaded

Hartree fock theory