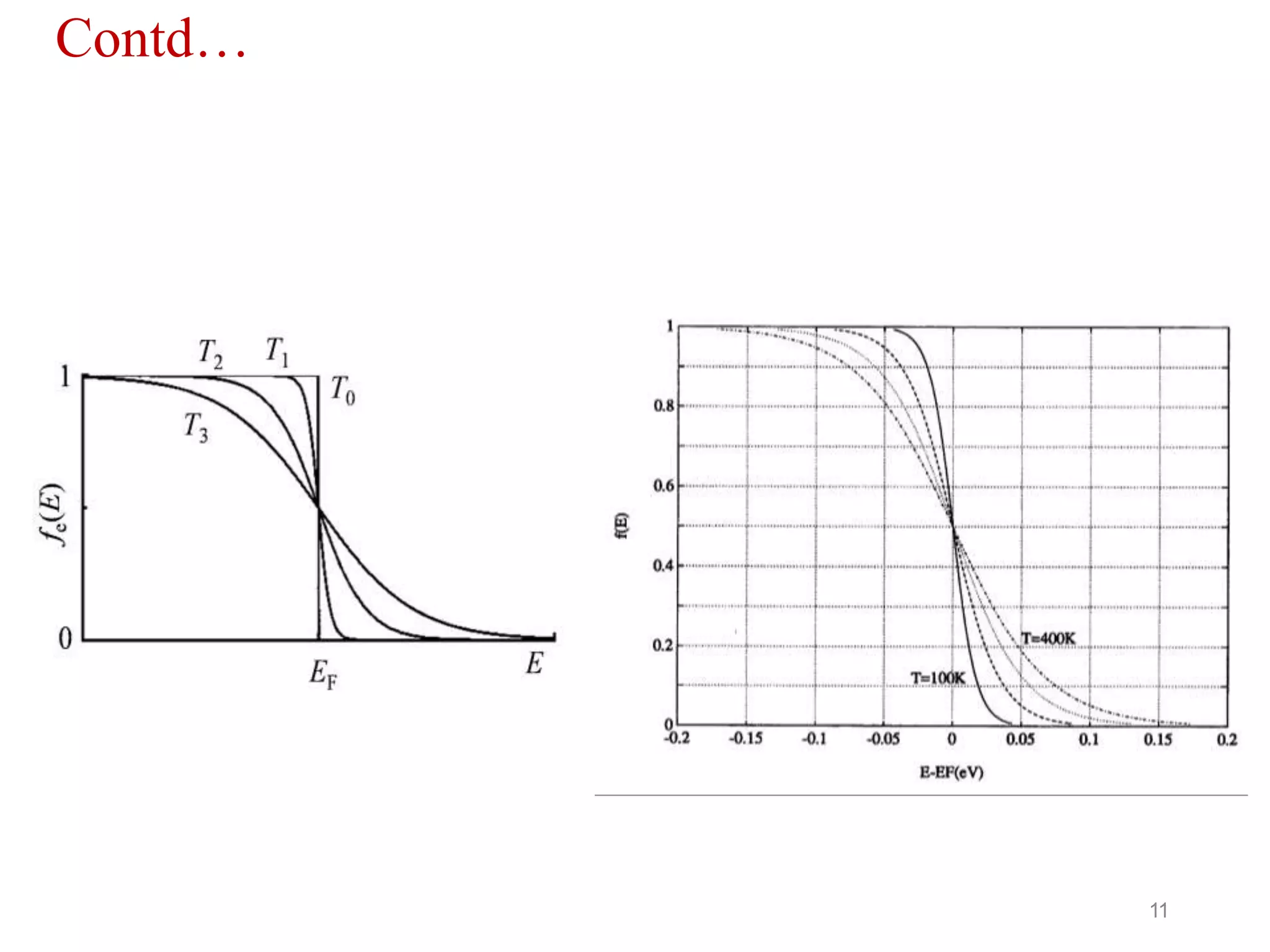
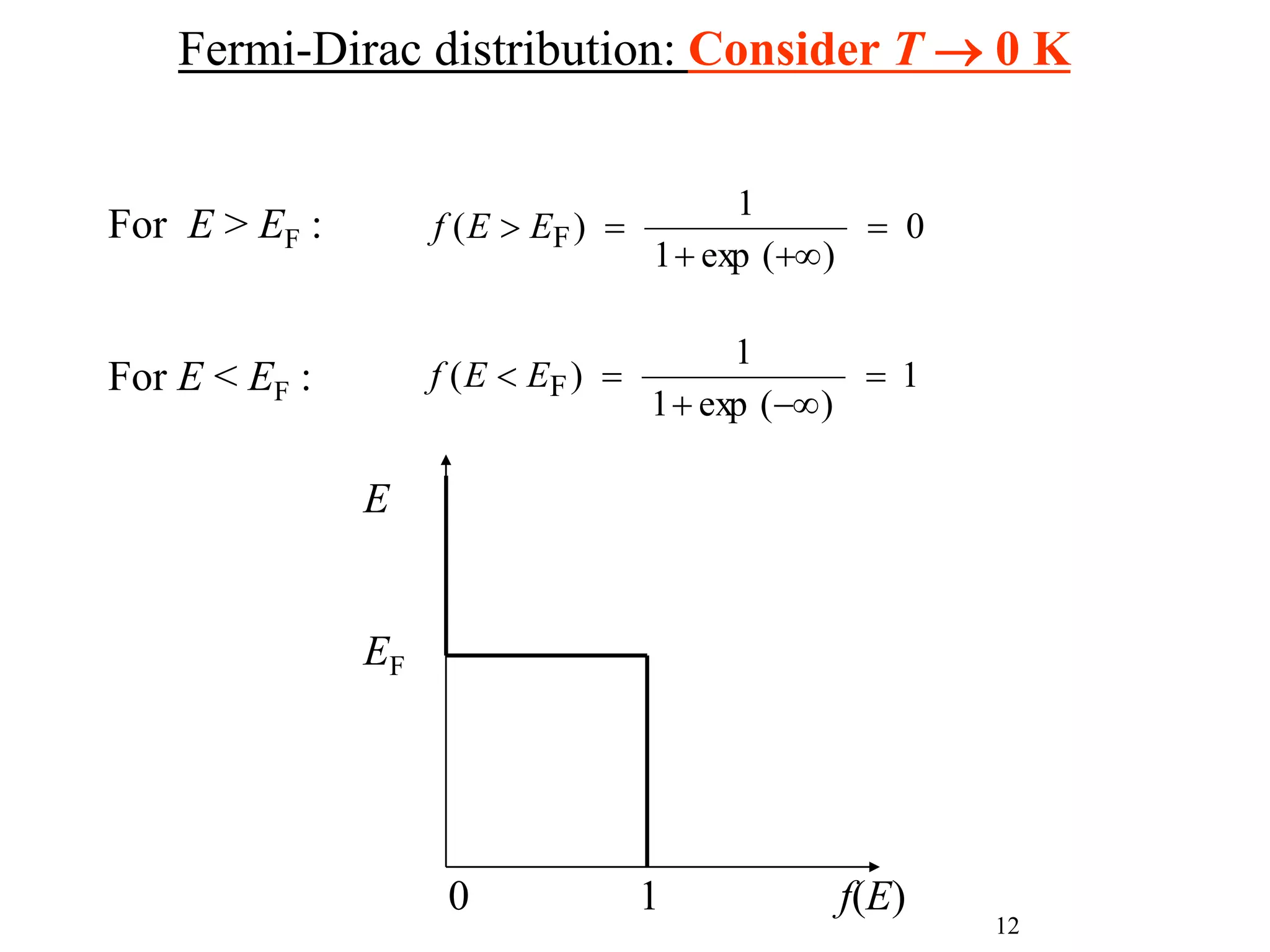
This document introduces the Fermi-Dirac distribution function. It begins by discussing basic concepts like the Fermi level and Fermi energy. It then covers Fermi and Bose statistics, and the postulates of Fermi particles. The derivation of the Fermi-Dirac distribution function is shown, which gives the probability of a quantum state being occupied at a given energy and temperature. Graphs are presented showing how the distribution varies with different temperatures. The classical limit of the distribution is discussed. References are provided at the end.

1. Presented by-
Md Ahsan Halimi
Scholar No: 19-3-04-105
Dept. of ECE, NIT Silchar
“Introduction of Fermi Dirac Distribution Function”
1

2. Contents
Some Basic Concept
Fermi-statistics and Bose Statistics
Postulates of Fermi particles
Fermi Dirac Distribution Function
Conclusion
References
2

3. Some basic concepts
 Fermi level :- Fermi level is the highest energy state occupied by
electrons in a material at absolute zero temperature.
 Fermi energy:-This is the maximum energy that an electron can
have at 0K. i.e. the energy of fastest moving electron at 0K. It is
given by,
𝐸 𝐹 =
1
2
𝑚𝑣 𝐹
2
 Fermi velocity (𝑣 𝐹):- It is the velocity of electron at Fermi level.
 The band theory of solids gives the picture that there is a sizable
gap between the Fermi level and the conduction band of the
semiconductor. At higher temperatures, a larger fraction of the
electrons can bridge this gap and participate in electrical
conduction.
3

4. Fermi-statistics and Bose Statistics
 The wave function of a system of identical particles must be either
symmetrical (Bose) or antisymmetrical (Fermi) in permutation of a
particle of the particle coordinates (including spin). It means that there
can be only the following two cases:
1. Fermi-Dirac Distribution
2. Bose-Einstein Distribution
 The differences between the two cases are determined by the nature of
particle. Particles which follow Fermi-statistics are called Fermi-
particles (Fermions) and those which follow Bose-statistics are called
Bose- particles (Bosones).
 Electrons, positrons, protons and neutrons are Fermi-particles, whereas
photons are Bosons. Fermion has a spin 1/2 and boson has integral spin.
Let us consider this two types of statistics consequently.
4

5. Different types of systems considered
 Distinguishable particles >(Fermions when spin is not
considered)
 Indistinguishable particles that obey Pauli exclusion principle
> (Fermions)
 Indistinguishable particles that doesn't obey Pauli exclusion principle
>(Bosons)
5

6. Postulates of Fermi Particle
 Particles are indistinguishable.
 Particles obey Pauli principle.
 Each quantum state can have only one particle.
 Each particle has one half spin.
 𝒈𝒊 be the quantum states associated with 𝒊 𝒕𝒉
energy
level.
 𝑵𝒊 is the no. of particles associated with 𝒊 𝒕𝒉 energy level.
 For a particular value of N, there is only one
distribution
6
N2 NnN1 ……………….

7. Fermi -Dirac distribution function
(Derivation)
Consider now the ith energy level with degeneracy gi. For this level,
the total no. of ways of arranging the particles is:
Consider all energy level, the permutation among themselves Now
the Ni particles can have Ni! Permutations
We now apply, the other two assumptions, namely conservation of
particles and energy.
7
)!(
!
)1)......(2)(1(
ii
i
iiiii
Ng
g
Ngggg


 

n
i iii
i
n
NgN
g
NNNNQSo
1
321
)!(!
!
),.......,,(,
constUEN
constNN
i
i
i
i
i





8. Contd…
 Stirling approximation (x>>1)
 Lagrangian multiplier method for lnQ
 Now we proceed in the standard fashion, by applying Stirling’s
approximation to lnQ, and then using the method of Lagrange
multipliers to maximize Q.
8
0ln
11









 
n
i
ii
j
n
i
i
jj
NE
N
N
N
Q
N

XXXX  ln!ln
𝑔𝑗
𝑁𝑗
= 1 + 𝑒−(𝛼+𝛽𝐸 𝑗)
𝑁𝑗
𝑔𝑗
=
1
1 + 𝑒−(𝛼+𝛽𝐸 𝑗)

9. Contd…
For i=j,
𝑁𝑖
𝑔𝑖
=
1
1 + 𝑒−(𝛼+𝛽𝐸 𝑖)
=
1
1 + 𝑒(𝐸 𝑖−𝐸 𝐹)/𝑘𝑇
;
𝛼 =
𝐸 𝐹
𝑘𝑇
, 𝛽 = −
1
𝑘𝑇
And because energy level is continuous,
𝑁 𝐸 𝑑𝐸 =
𝑔 𝐸 𝑑𝐸
1 + 𝑒(𝐸−𝐸 𝐹)/𝑘𝑇
 g(E)dEis the number of available states in the energy range E and E+dE
 Number of particles between E and E+dE is given by
N(E)dE=f(E)*g(E)dE
 f(E) is the probability that a state at energy E is occupied by a particle
𝑓 𝐸 =
𝑁 𝐸
𝑔(𝐸)
=
1
1 + 𝑒(𝐸−𝐸 𝐹) 𝑘𝑇
9

10. Contd…
 Density of states tells us how many states exist at a given energy
E.
 The Fermi function f(E) specifies how many of the existing states
at the energy E will be filled with electrons. Whereas (1- f(E))
gives the probability that energy state E will be occupied by a
hole.
 The function f(E) specifies, under equilibrium conditions, the
probability that an available state at an energy E will be occupied
by an electron. It is a probability distribution function.
10

11. Contd…
11

12. 12
Fermi-Dirac distribution: Consider T  0 K
For E > EF :
For E < EF :
0
)(exp1
1
)( F 

 EEf
1
)(exp1
1
)( F 

 EEf
E
EF
0 1 f(E)

13. 13
Classical limit
For sufficiently large  we will have (-)/kT>>1, and in this limit
kT/)(
e)f( 
 
 (5.47)
This is just the Boltzmann distribution. The high-energy tail of the Fermi-Dirac
distribution is similar to the Boltzmann distribution. The condition for the
approximate validity of the Boltzmann distribution for all energies  0 is that
1 kT/
e  (5.48)

14. Fermi -Dirac distribution function:-
14
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Fermi Dirac Distribution function
Energy (eV)
FermiDiracDistributionfunction
T1=50 K
T2=100 K
T3=300 K
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Fermi Dirac Distribution function of particle density with Energy
Energy (eV)
FermiDiracDistributionfunction
T1=50 K
T2=100 K
T3=300 K

15. References
1. Statistical Physics (2nd Edition), F. Mandl, Manchester
Physics, John Wiley & Sons, 2008,
ISBN 9780471915331.
2. H.J.W. Muller-Kirsten, Basics of Statistical Physics,
2nd ed., World Scientific, ISBN: 978-981-4449-53-3.
15

16. Thank You
16