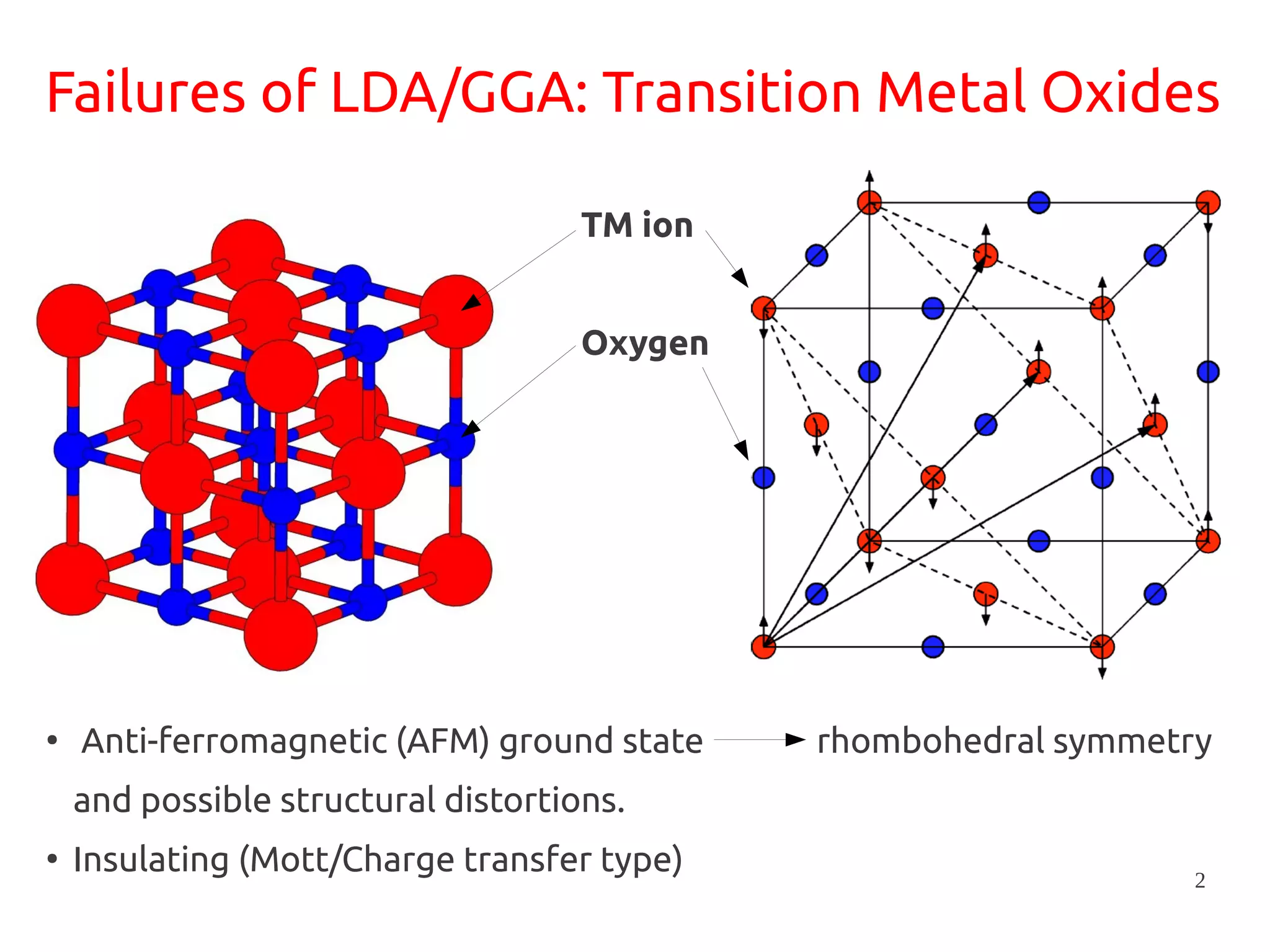
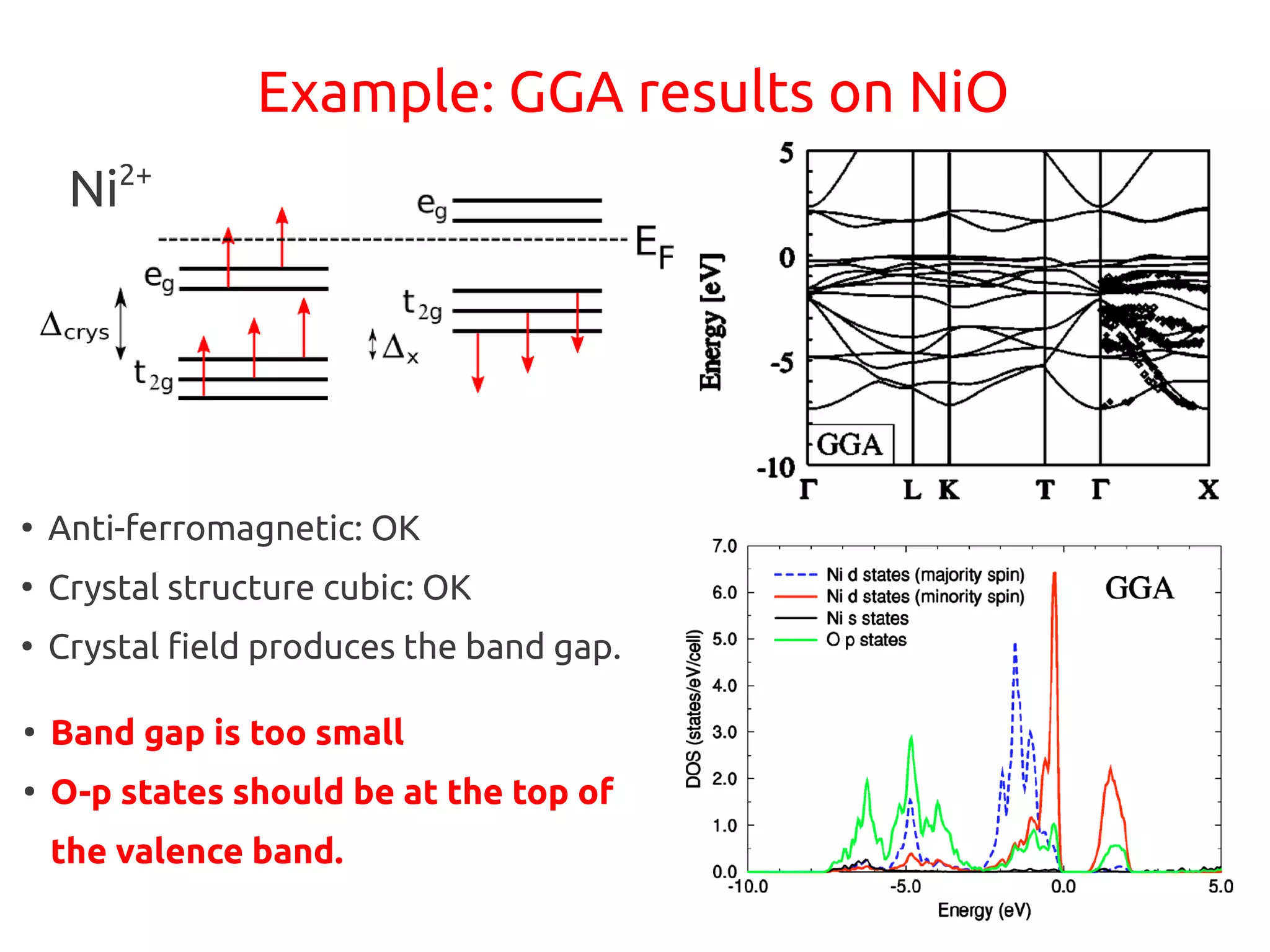
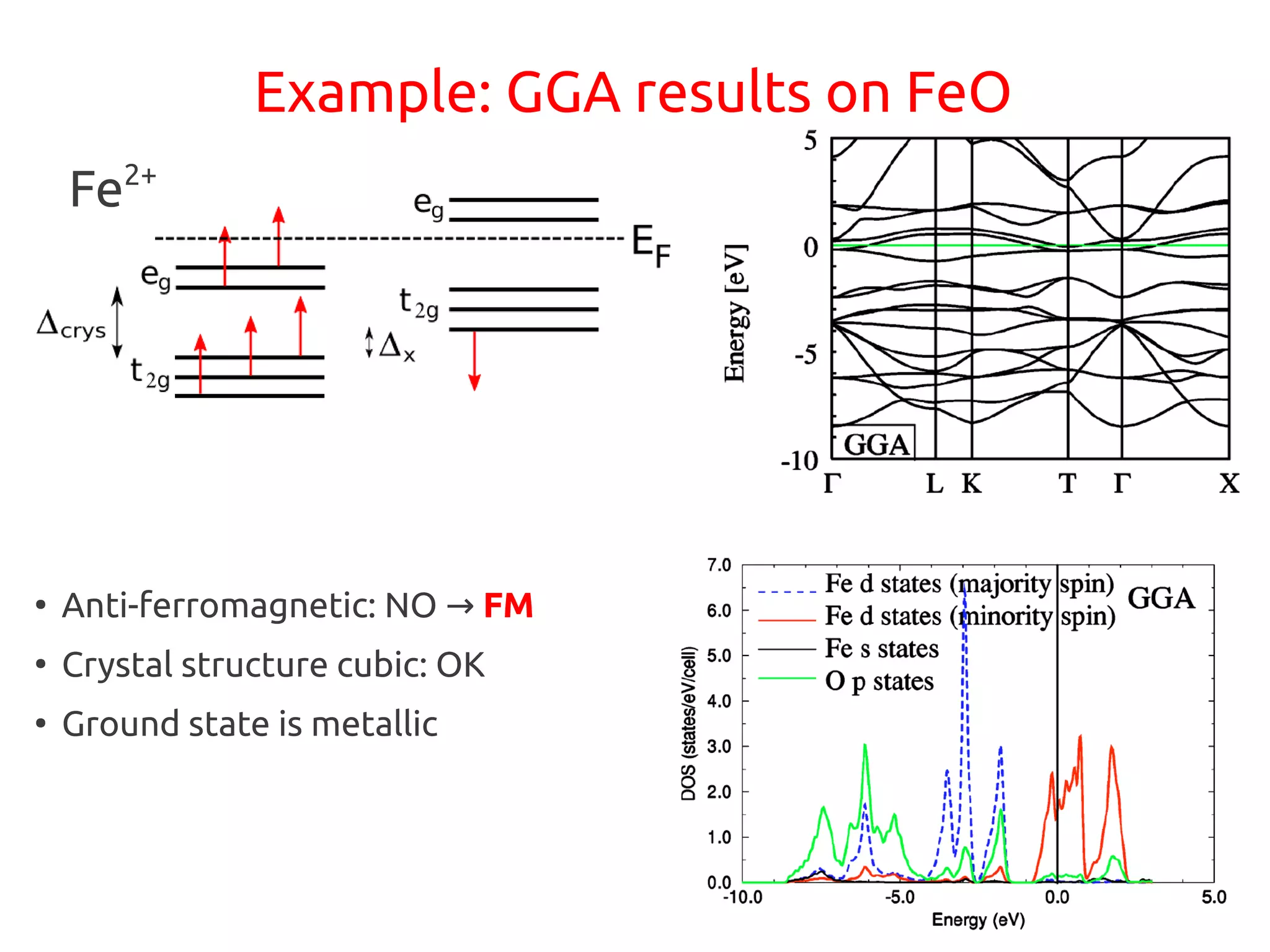
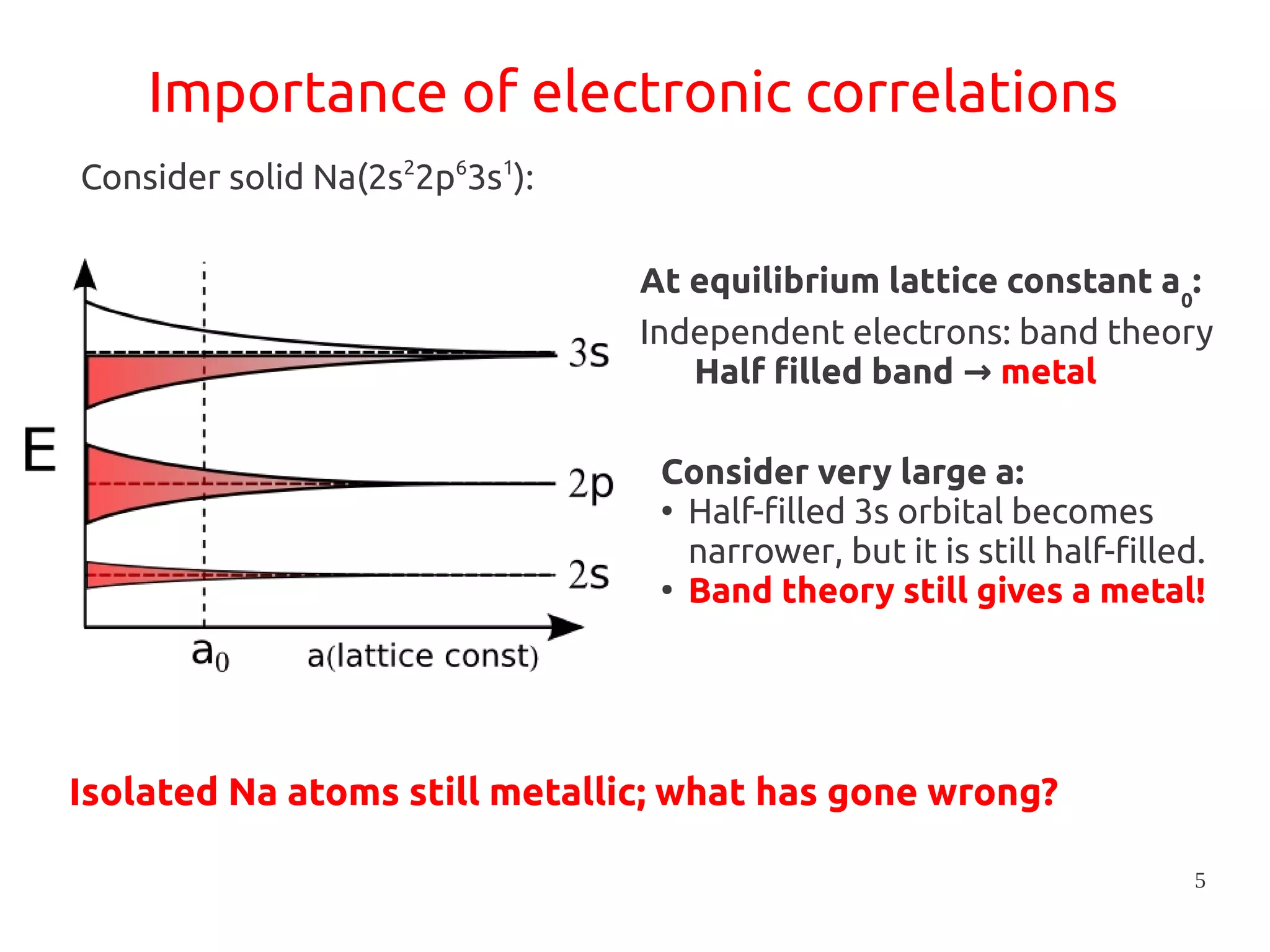
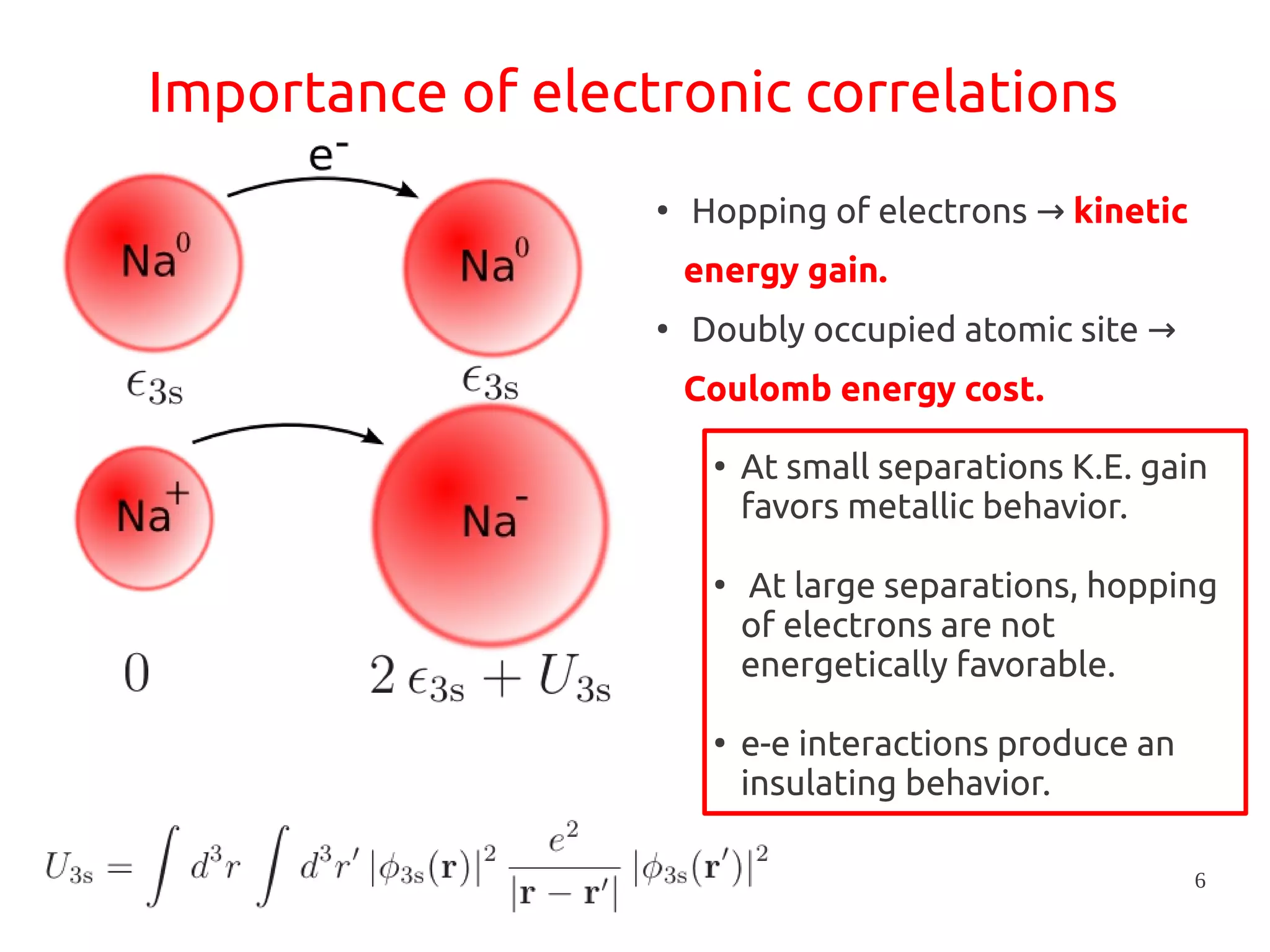
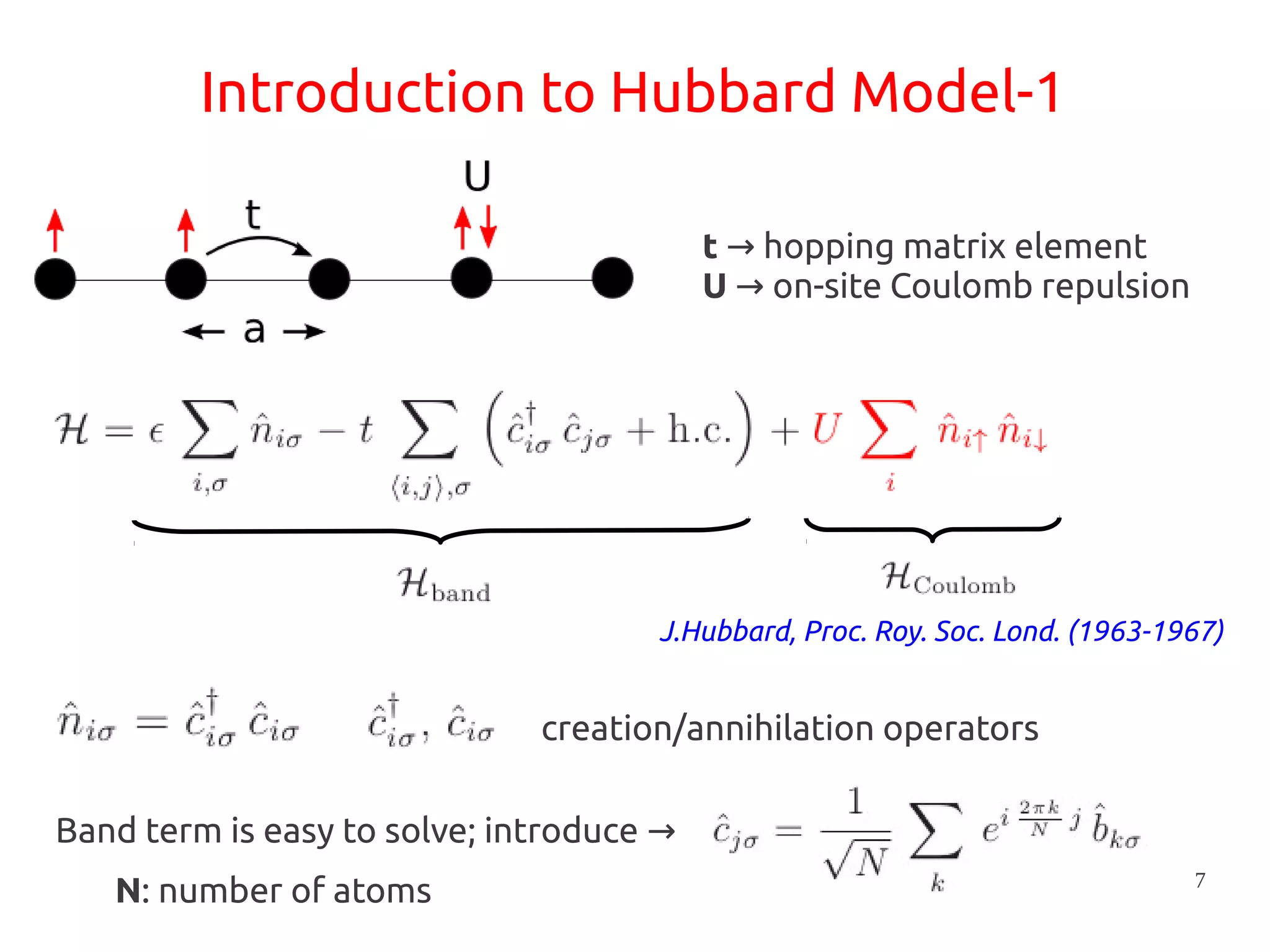
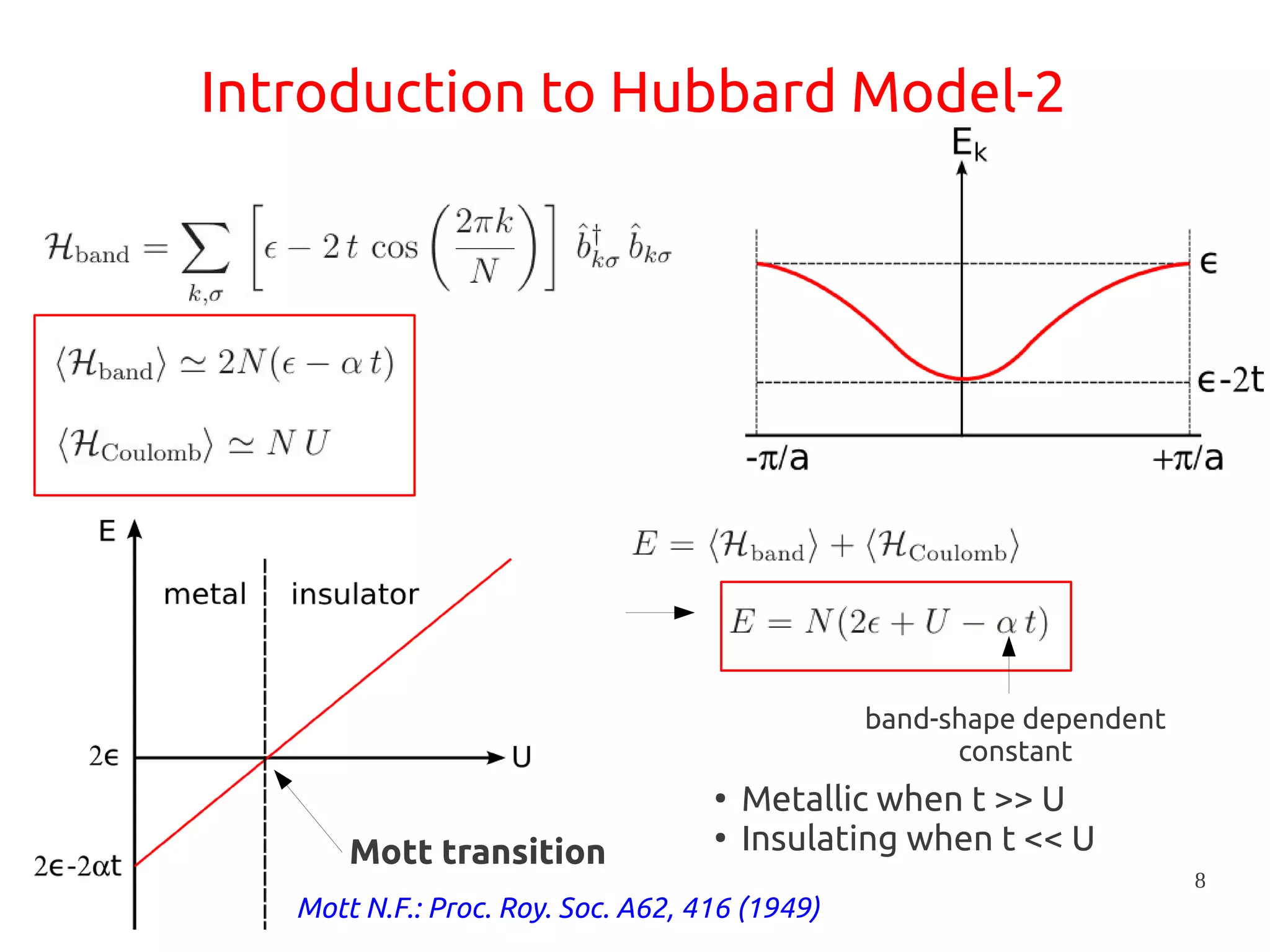
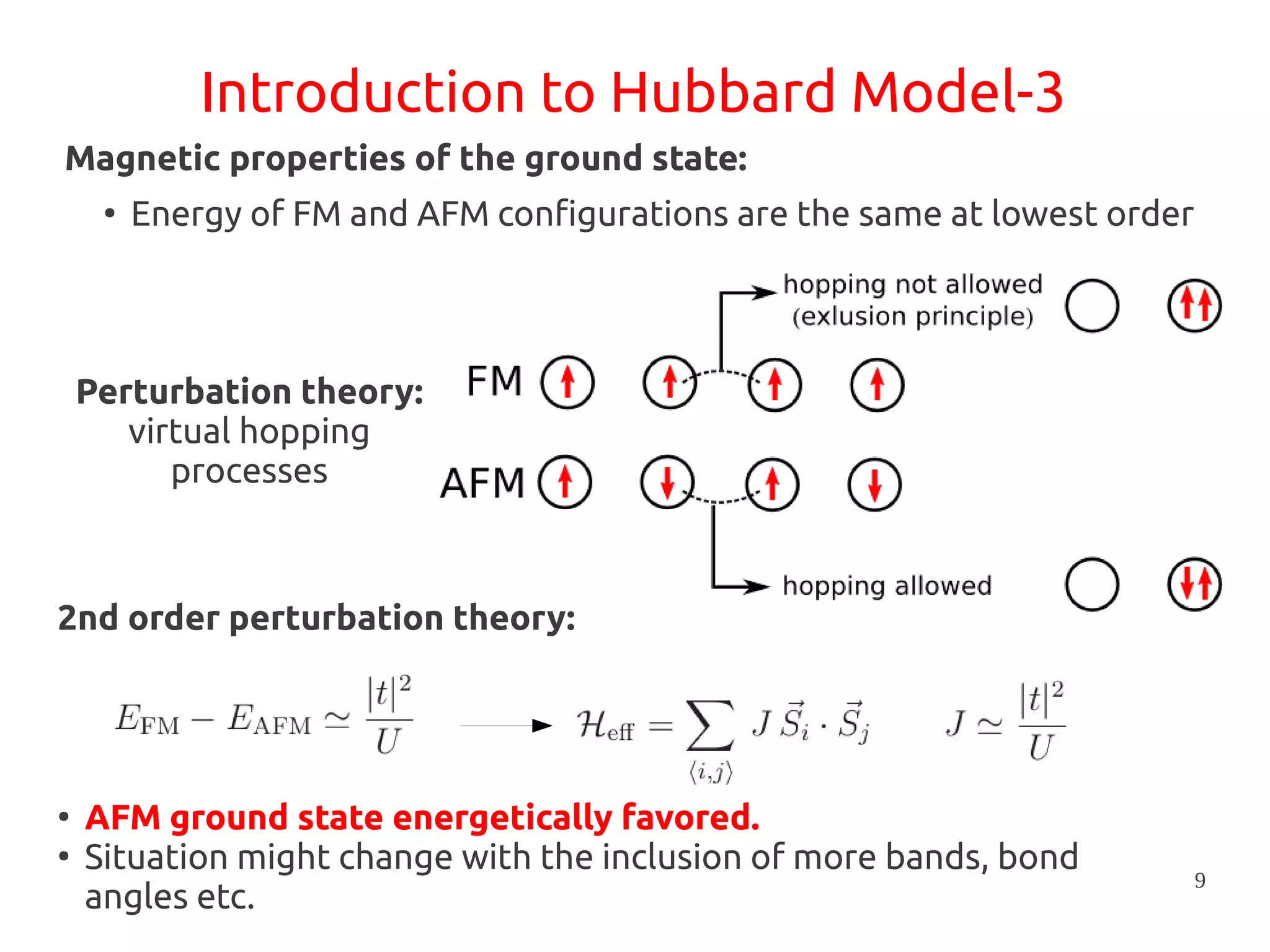
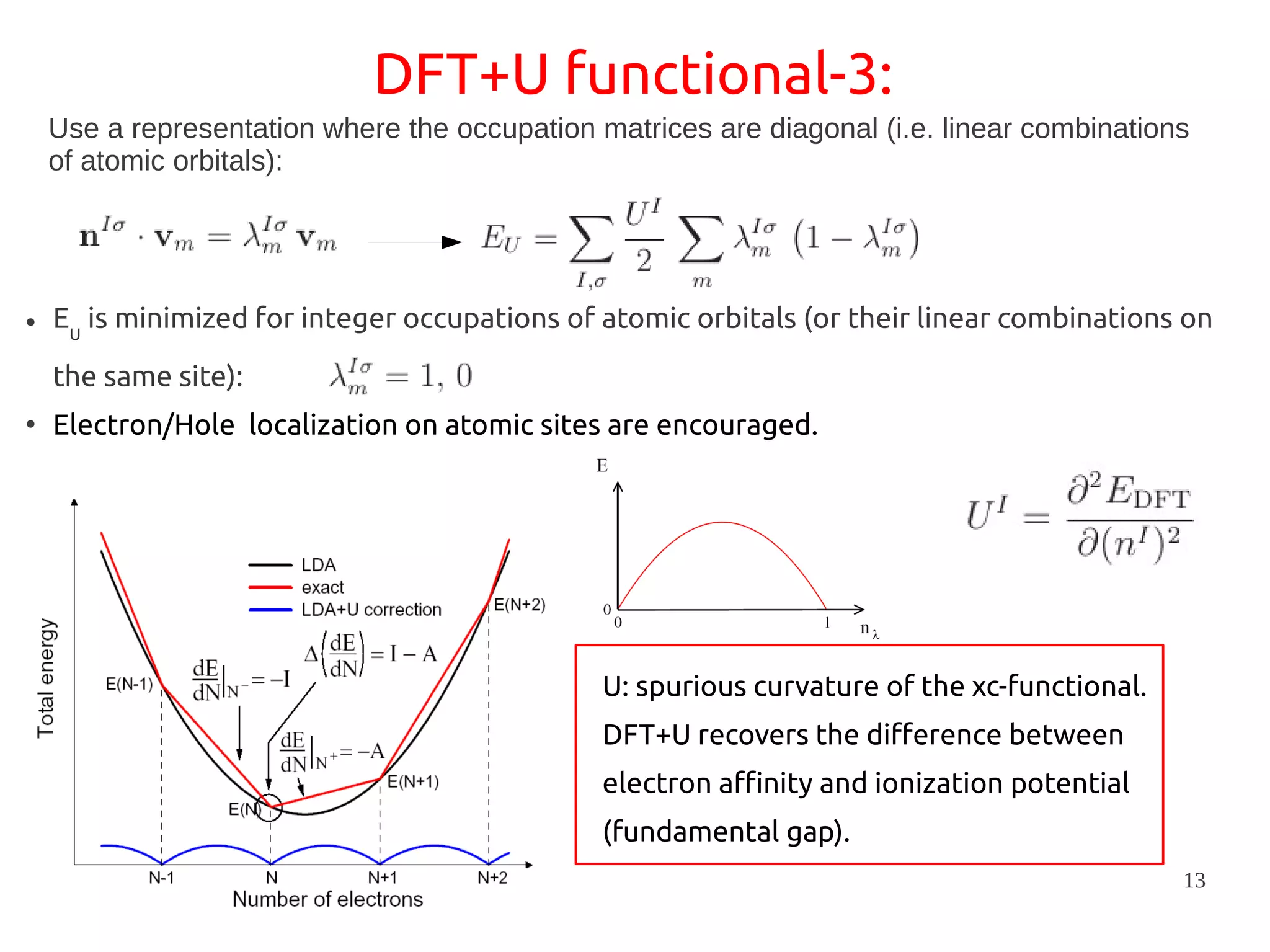
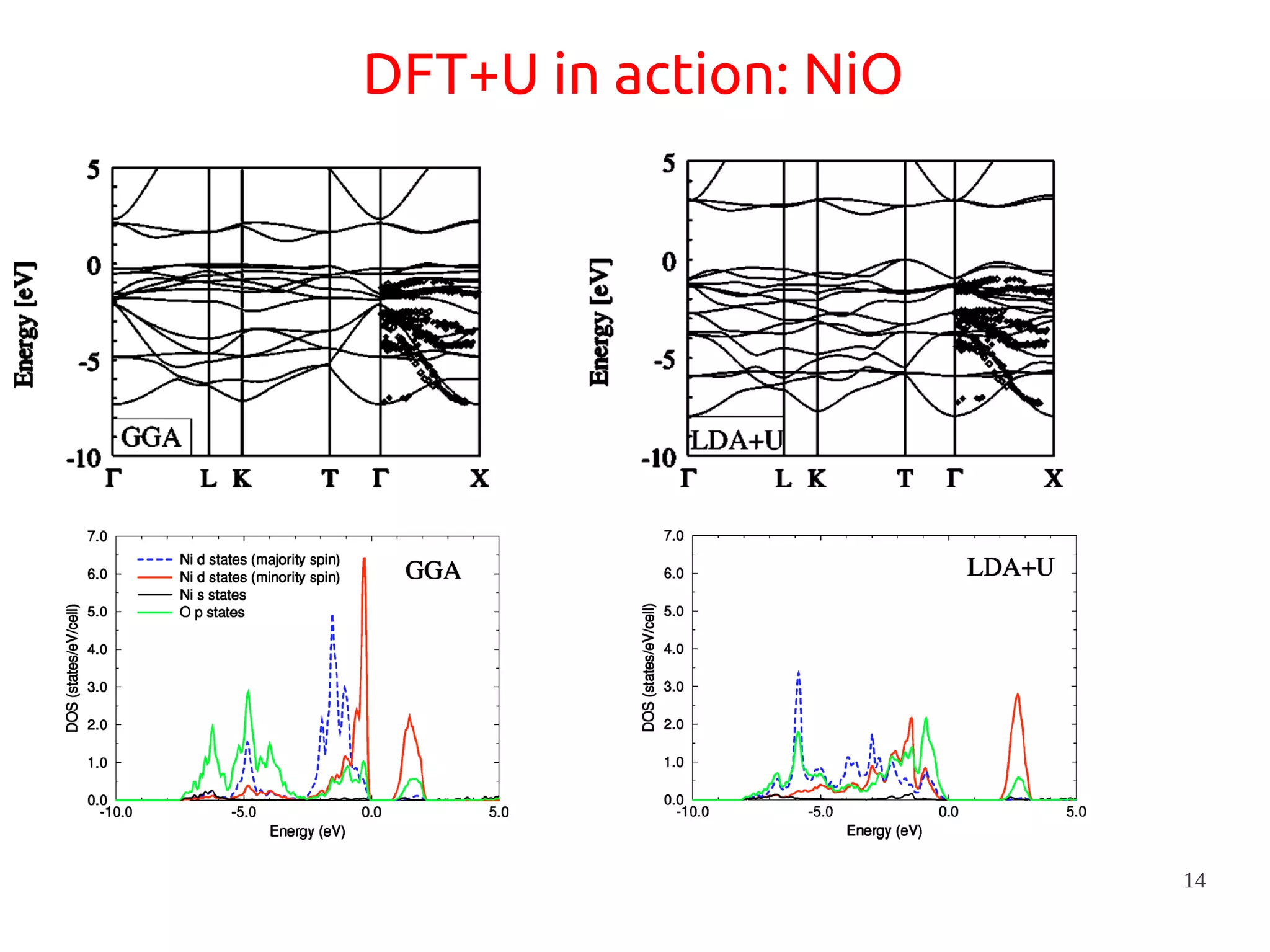
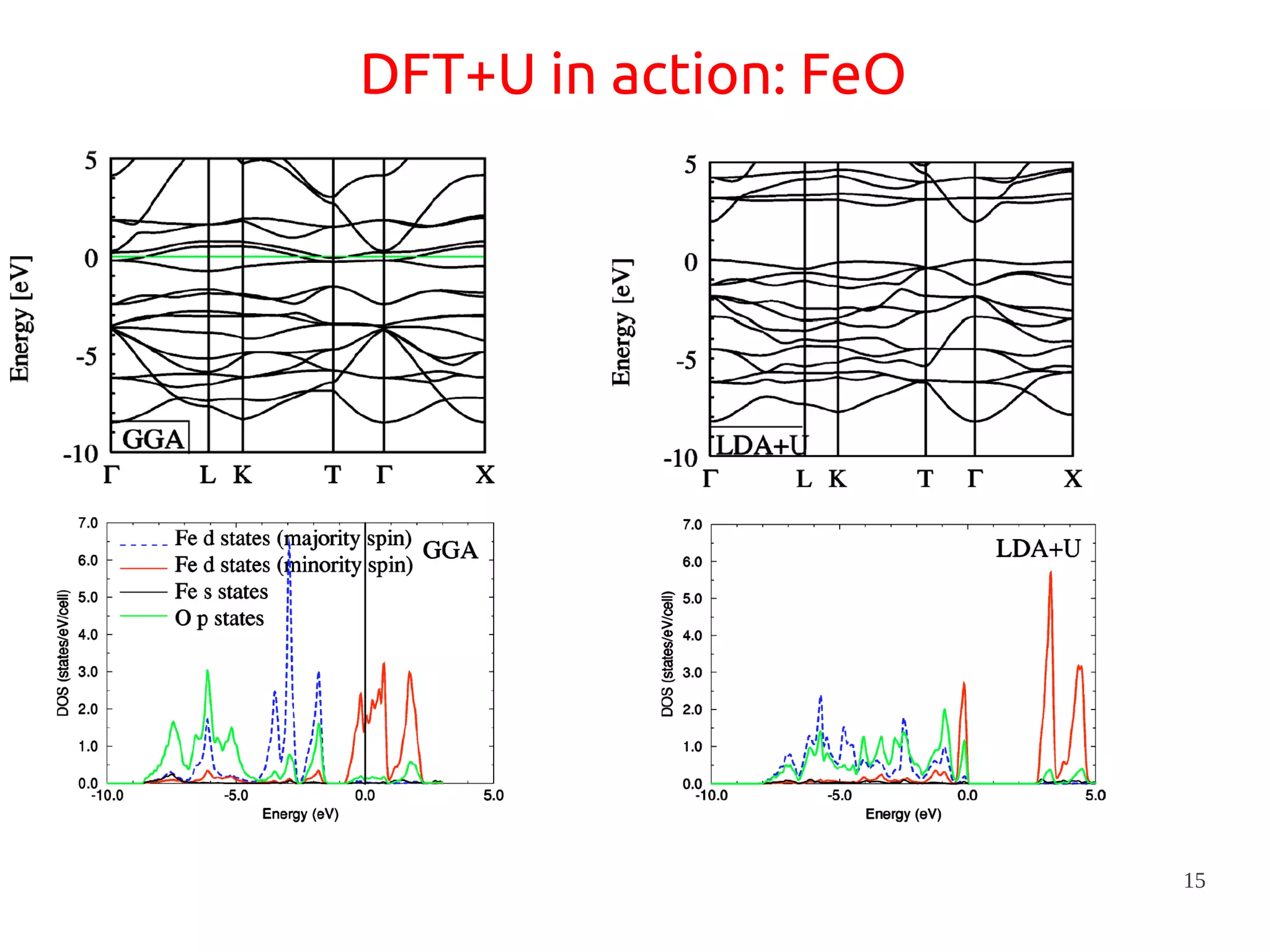
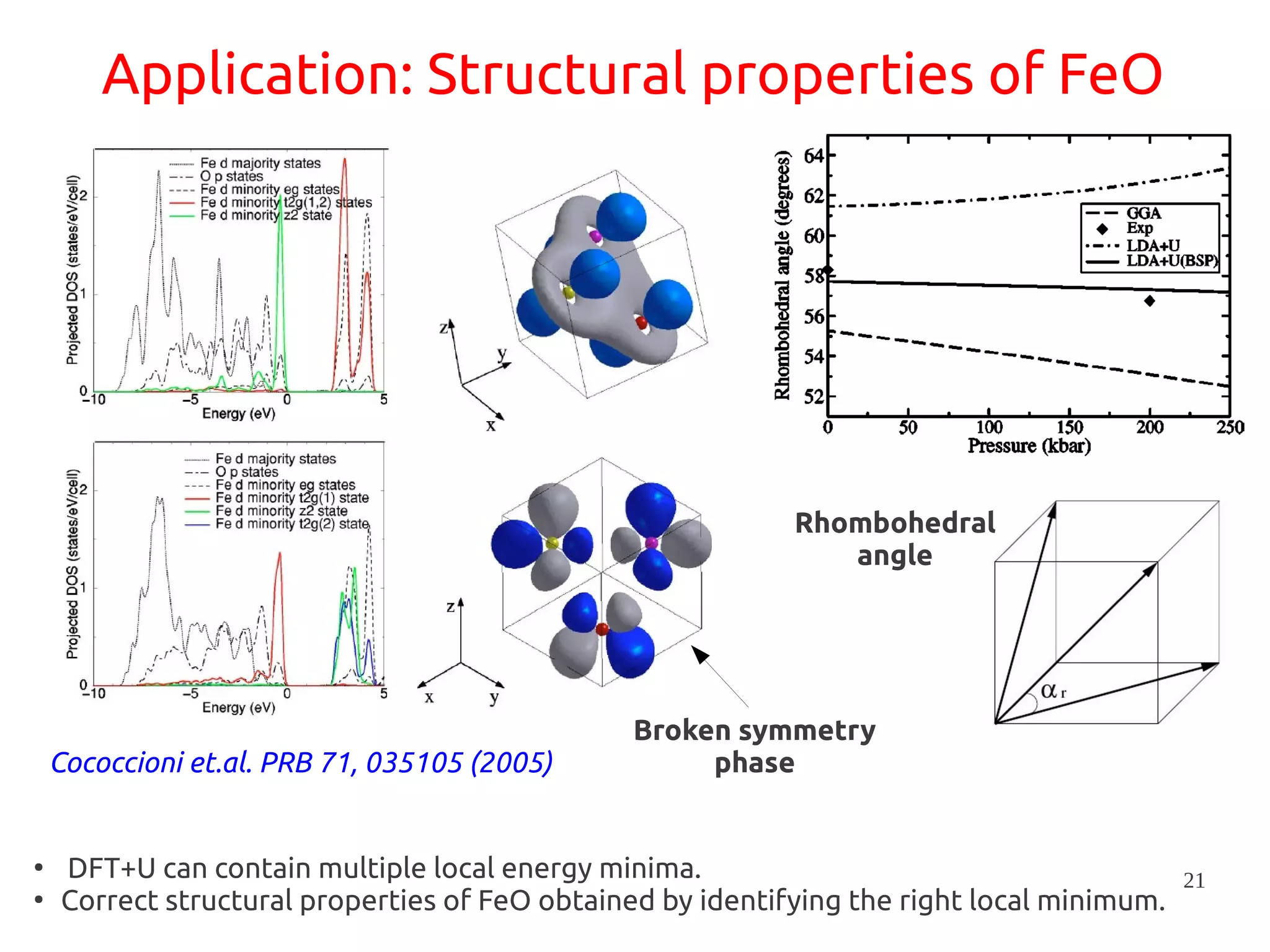
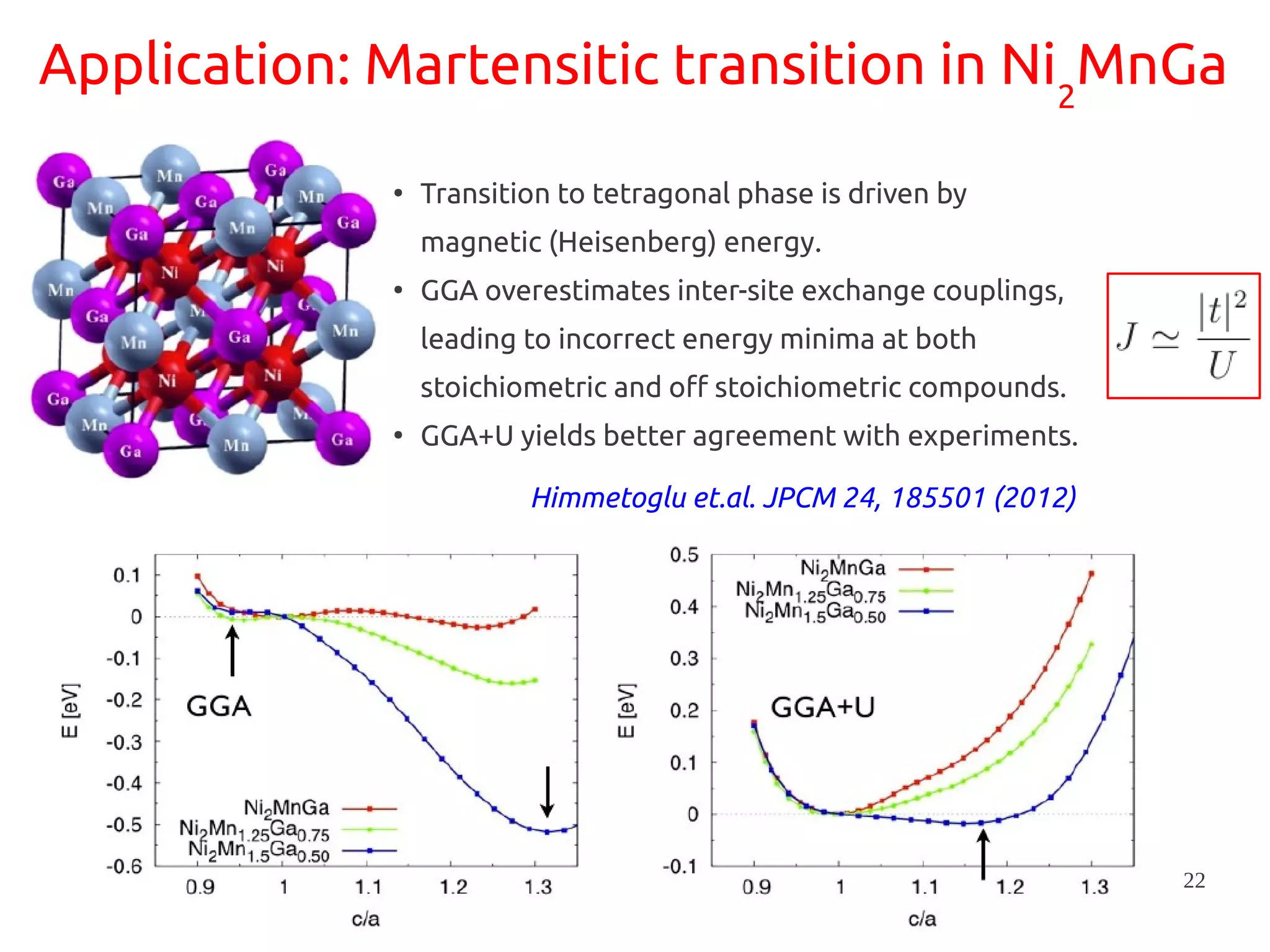
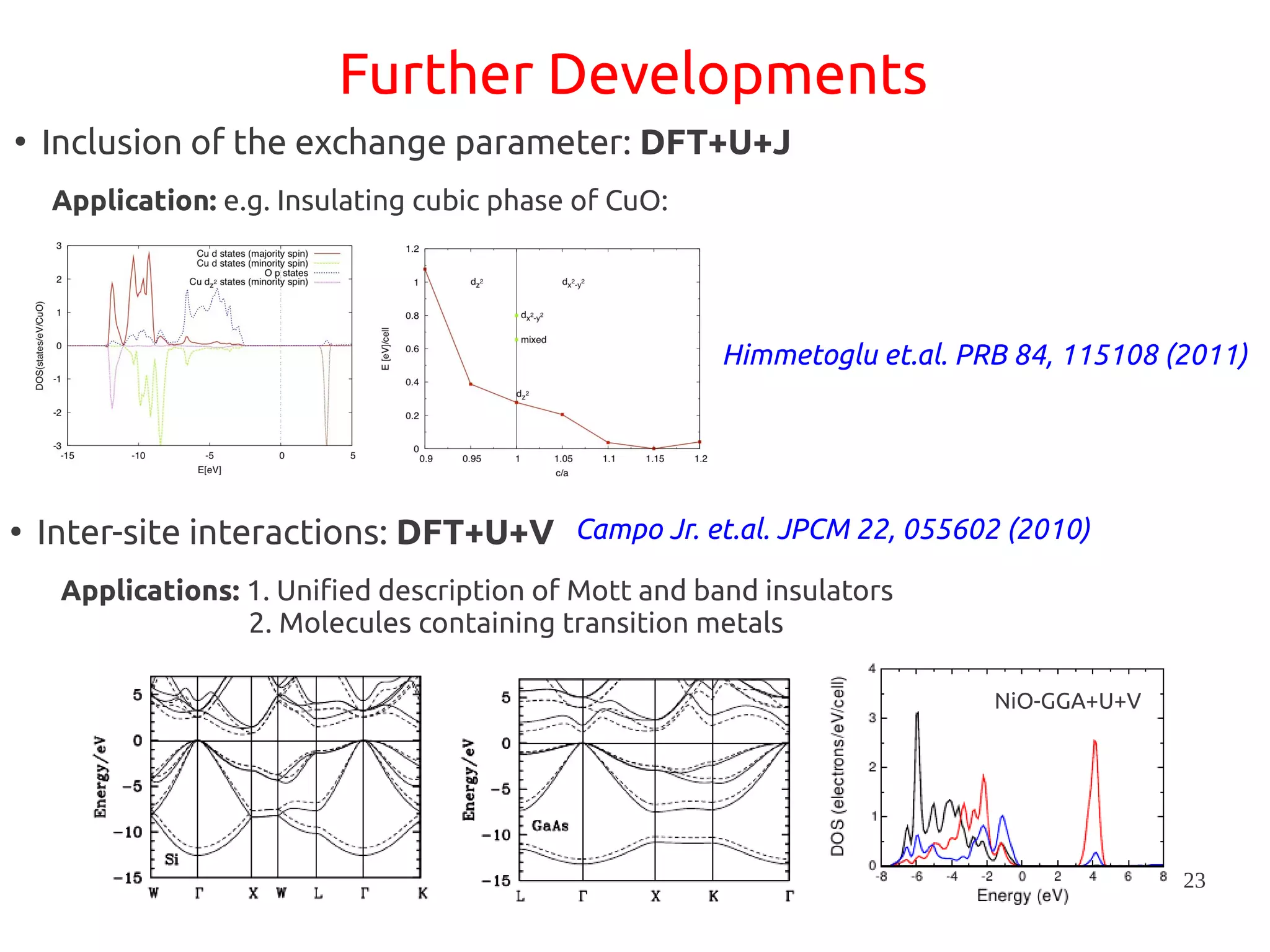
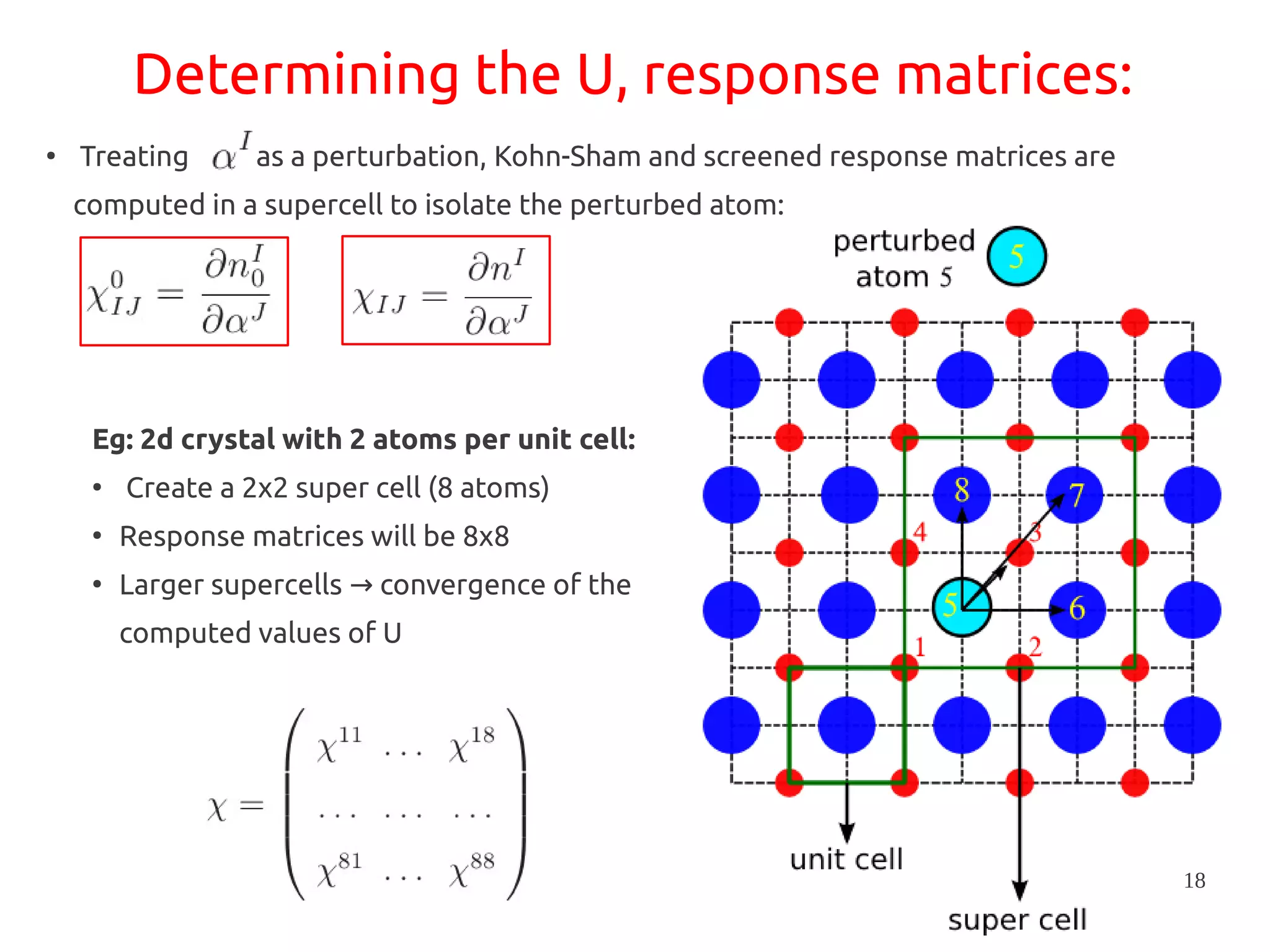
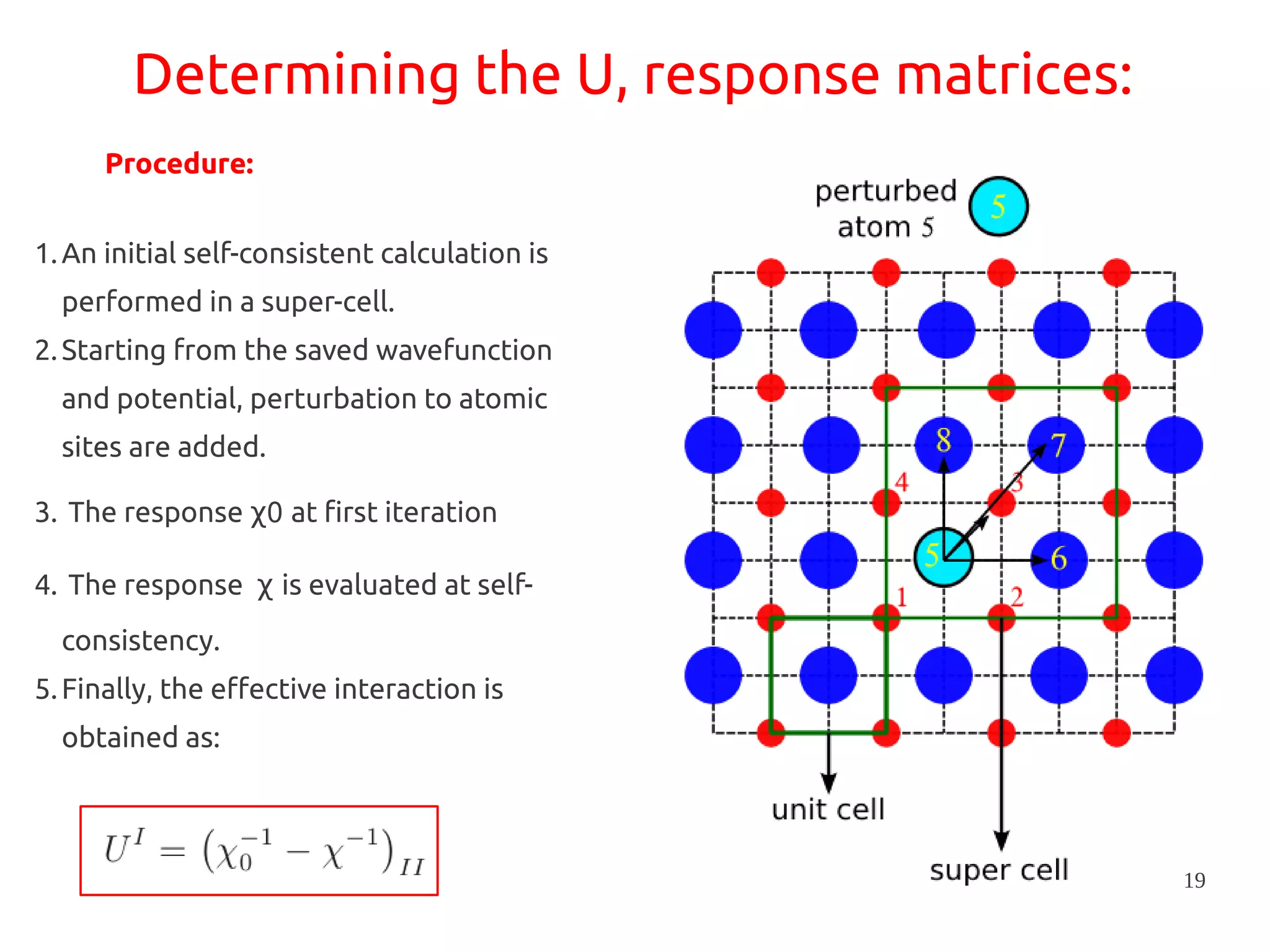
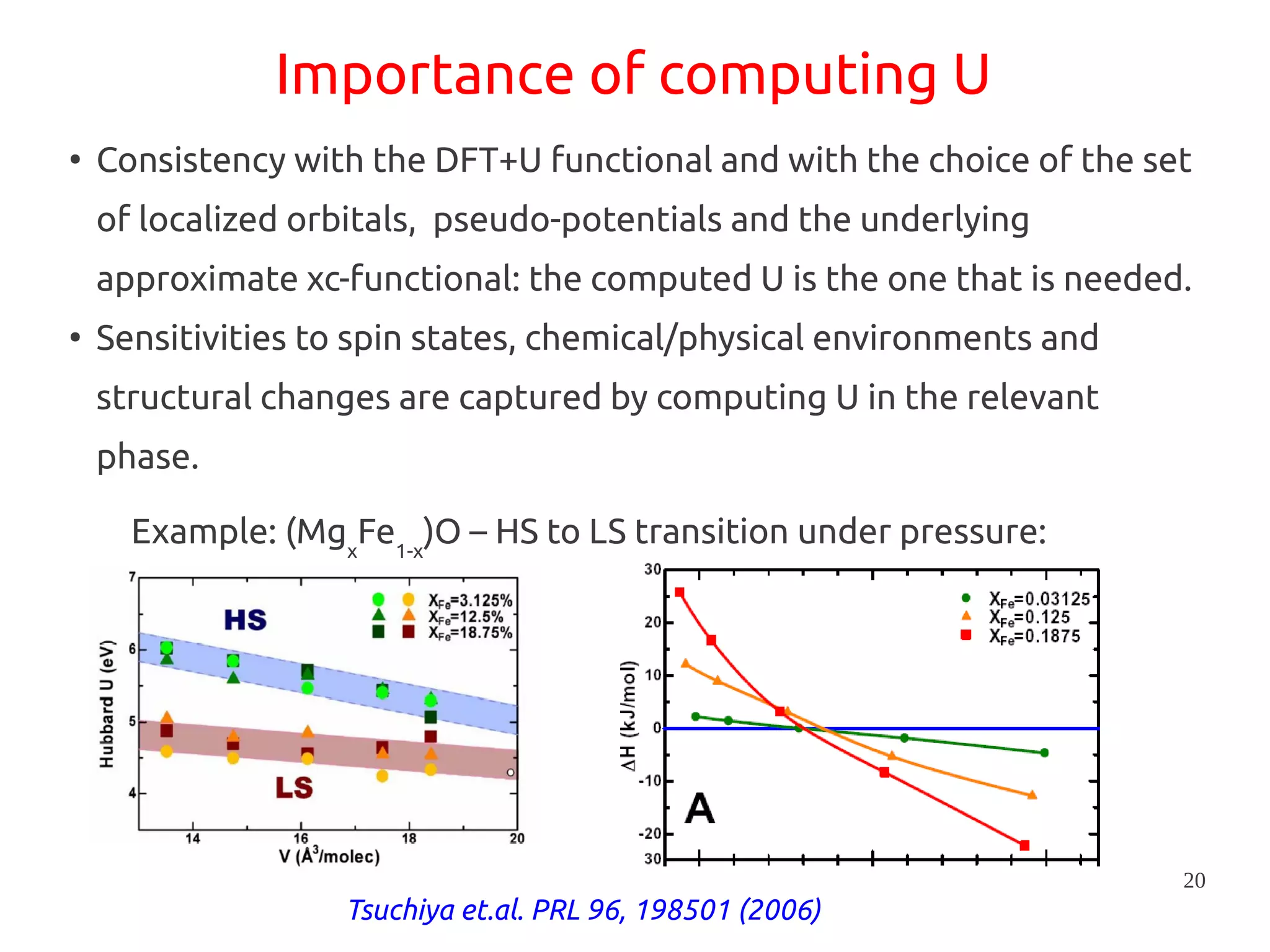
1. DFT+U is a method that adds Hubbard corrections to DFT to better account for localized electrons and electronic correlations in transition metal oxides that LDA/GGA cannot describe accurately. 2. It introduces an on-site Coulomb repulsion term U to the energy functional that favors electron localization and integer orbital occupations. 3. The U parameter can be computed using linear response theory by perturbing occupation matrices and evaluating screened response matrices in a supercell calculation.

1. 1
Advanced xc-functionals: DFT+U
Burak Himmetoglu
●
Well known failures of LDA/GGA: transition metal oxides
●
Importance of electronic correlations: Mott transition
●
Introduction to Hubbard Model
●
DFT+U: Formulation and implementation
●
Calculation of U
●
Some examples and applications

2. 2
Failures of LDA/GGA: Transition Metal Oxides
TM ion
Oxygen
●
Anti-ferromagnetic (AFM) ground state rhombohedral symmetry
and possible structural distortions.
●
Insulating (Mott/Charge transfer type)

3. 3
Example: GGA results on NiO
●
Anti-ferromagnetic: OK
●
Crystal structure cubic: OK
●
Crystal field produces the band gap.
●
Band gap is too small
●
O-p states should be at the top of
the valence band.
Ni2+

4. 4
Example: GGA results on FeO
Fe2+
●
Anti-ferromagnetic: NO → FM
●
Crystal structure cubic: OK
●
Ground state is metallic

5. 5
Importance of electronic correlations
Consider solid Na(2s2
2p6
3s1
):
At equilibrium lattice constant a0
:
Independent electrons: band theory
Half filled band → metal
Consider very large a:
●
Half-filled 3s orbital becomes
narrower, but it is still half-filled.
●
Band theory still gives a metal!
Isolated Na atoms still metallic; what has gone wrong?

6. 6
Importance of electronic correlations
●
Hopping of electrons → kinetic
energy gain.
●
Doubly occupied atomic site →
Coulomb energy cost.
●
At small separations K.E. gain
favors metallic behavior.
●
At large separations, hopping
of electrons are not
energetically favorable.
●
e-e interactions produce an
insulating behavior.

7. 7
Introduction to Hubbard Model-1
t hopping matrix element→
U on-site Coulomb repulsion→
Band term is easy to solve; introduce →
creation/annihilation operators
N: number of atoms
J.Hubbard, Proc. Roy. Soc. Lond. (1963-1967)

8. 8
Introduction to Hubbard Model-2
●
Metallic when t >> U
●
Insulating when t << UMott transition
band-shape dependent
constant
Mott N.F.: Proc. Roy. Soc. A62, 416 (1949)

9. 9
Introduction to Hubbard Model-3
Magnetic properties of the ground state:
2nd order perturbation theory:
Perturbation theory:
virtual hopping
processes
●
AFM ground state energetically favored.
●
Situation might change with the inclusion of more bands, bond
angles etc.
●
Energy of FM and AFM configurations are the same at lowest order

10. 10
LDA/GGA Failures and DFT+U:
●
LDA/GGA approximations over delocalize electrons serious problem→
for localized d and f states of transition metals.
●
On-site e-e interactions (i.e. U in Hubbard model), are not well
accounted for.
●
Energy functional contains self-interaction.
●
GGA/LDA describes independent
electronic contributions well.
●
Addition of Hubbard model based
corrections on top of LDA/GGA to
correct for localized electrons.
The idea:

11. 11
DFT+U functional-1:
LDA/GGA
functional
Hubbard
correction
subtract
“double counting”
● Ehub
Contains an energy functional based on the Hubbard model→
● Edc
Averaged e-e interaction energy to be subtracted (already contained in E→ DFT
)
atomic orbital centered on I
KS states
occupation of KS states
occupation matrices:

12. 12
DFT+U functional-2:
First approximation:
→ Ignore exchange type terms
→ Average over atomic orbitals
The double counting term is the sum of the averaged on-site interaction terms:
Collecting the contributions:
With these approximations, the Hubbard energy becomes:

13. 13
DFT+U functional-3:
Use a representation where the occupation matrices are diagonal (i.e. linear combinations
of atomic orbitals):
● EU
is minimized for integer occupations of atomic orbitals (or their linear combinations on
the same site):
●
Electron/Hole localization on atomic sites are encouraged.
U: spurious curvature of the xc-functional.
DFT+U recovers the difference between
electron affinity and ionization potential
(fundamental gap).

14. 14
DFT+U in action: NiO

15. 15
DFT+U in action: FeO

16. 16
Determining the U:
●
We have seen that U corresponds to the curvature of the DFT functional
●
Then, we can compute energy derivatives to compute U from LDA/GGA
→ linear response
From self-consistent
ground state
(screened response)
Kohn-Sham response:
(due to re-hybridization
of orbitals)

17. 17
Determining the U, 2nd derivatives:
●
2nd derivative of energy is not easily accessible.
●
Instead, we use a Legendre transformed functional to compute first
derivatives:
Legendre transform
Potential shift
in order to perturb the
number of states on site I
Cococcioni et.al. PRB 71, 035105 (2005)

18. 18
Determining the U, response matrices:
●
Treating as a perturbation, Kohn-Sham and screened response matrices are
computed in a supercell to isolate the perturbed atom:
Eg: 2d crystal with 2 atoms per unit cell:
●
Create a 2x2 super cell (8 atoms)
●
Response matrices will be 8x8
●
Larger supercells convergence of the→
computed values of U

19. 19
1.An initial self-consistent calculation is
performed in a super-cell.
2.Starting from the saved wavefunction
and potential, perturbation to atomic
sites are added.
3. The response 0χ at first iteration
4. The response χ is evaluated at self-
consistency.
5.Finally, the effective interaction is
obtained as:
Procedure:
Determining the U, response matrices:

20. 20
Importance of computing U
●
Consistency with the DFT+U functional and with the choice of the set
of localized orbitals, pseudo-potentials and the underlying
approximate xc-functional: the computed U is the one that is needed.
●
Sensitivities to spin states, chemical/physical environments and
structural changes are captured by computing U in the relevant
phase.
Example: (Mgx
Fe1-x
)O – HS to LS transition under pressure:
Tsuchiya et.al. PRL 96, 198501 (2006)

21. 21
Application: Structural properties of FeO
Broken symmetry
phase
●
DFT+U can contain multiple local energy minima.
●
Correct structural properties of FeO obtained by identifying the right local minimum.
Rhombohedral
angle
Cococcioni et.al. PRB 71, 035105 (2005)

22. 22
Application: Martensitic transition in Ni2
MnGa
●
Transition to tetragonal phase is driven by
magnetic (Heisenberg) energy.
●
GGA overestimates inter-site exchange couplings,
leading to incorrect energy minima at both
stoichiometric and off stoichiometric compounds.
●
GGA+U yields better agreement with experiments.
Himmetoglu et.al. JPCM 24, 185501 (2012)

23. 23
Further Developments
●
Inclusion of the exchange parameter: DFT+U+J
●
Inter-site interactions: DFT+U+V
Himmetoglu et.al. PRB 84, 115108 (2011)
Application: e.g. Insulating cubic phase of CuO:
Campo Jr. et.al. JPCM 22, 055602 (2010)
Applications: 1. Unified description of Mott and band insulators
2. Molecules containing transition metals
NiO-GGA+U+V