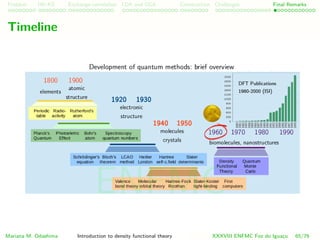
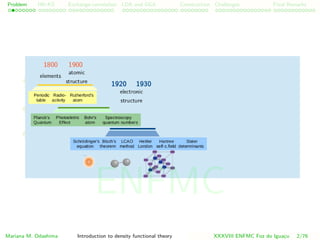
This document provides an introduction to density functional theory (DFT), detailing its historical context, key concepts, and foundational theorems such as the Hohenberg-Kohn theorem. It discusses various computational methods and challenges associated with approximating the electronic structure of many-body systems, including the Hartree and Kohn-Sham methods. The tutorial outlines the significance of exchange-correlation effects and the formulation of DFT as a practical approach to solving quantum mechanical problems in physics and chemistry.

1. XXXVIII ENFMC Brazilian Physical Society Meeting
Introduction to
density functional theory
Mariana M. Odashima
ENFMC

2. Problem HK-KS xc LDA Construction Challenges Final Remarks
This tutorial
Introduction to density-functional theory
Context and key concepts (1927-1930)
(Born-Oppenheimer, Hartree, Hartree-Fock, Thomas-Fermi)
Fundamentals (1964-1965)
(Hohenberg-Kohn theorem, Kohn-Sham scheme)
Approximations (≈ 1980-2010)
(local density and generalized gradient approximations (LDA and
GGA), construction of functionals)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 1/76
ENFMC

3. Problem HK-KS xc LDA Construction Challenges Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 2/76
ENFMC

4. Problem HK-KS xc LDA Construction Challenges Final Remarks
Dirac (1929)
“The general theory of quantum mechanics is
now almost complete (...) The underlying physi-
cal laws necessary for the mathematical theory of
a large part of physics and the whole of chemistry
are thus completely known, and the difficulty is
only that the exact application of these laws leads
to equations much too complicated to be soluble.
(...) It therefore becomes desirable that approxi-
mate practical methods of applying quantum me-
chanics should be developed, which can lead to
an explanation of the main features of complex
atomic systems without too much computation.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 3/76
ENFMC

5. Problem HK-KS xc LDA Construction Challenges Final Remarks
The electronic structure problem
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 4/76
ENFMC

6. Problem HK-KS xc LDA Construction Challenges Final Remarks
The electronic structure problem
Quantum many-body problem
of N interacting electrons: Ψel(r1, r2, ..., rN )
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 4/76
ENFMC

7. Problem HK-KS xc LDA Construction Challenges Final Remarks
The electronic structure problem
Quantum many-body problem
of N interacting electrons: Ψel(r1, r2, ..., rN )
Paradigms: atom / electron gas
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 4/76
ENFMC

8. Problem HK-KS xc LDA Construction Challenges Final Remarks
The electronic structure problem
Quantum many-body problem
of N interacting electrons: Ψel(r1, r2, ..., rN )
Paradigms: atom / electron gas
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 4/76
ENFMC

9. Problem HK-KS xc LDA Construction Challenges Final Remarks
The electronic structure problem
Quantum many-body problem
of N interacting electrons: Ψel(r1, r2, ..., rN )
Paradigms: atom / electron gas
Methods based on the wavefunction
(Hartree-Fock, CI, Coupled Cluster, MP2, QMC)
Methods based on the Green’s function, reduced density
matrix, density (density functional theory)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 4/76
ENFMC

10. Problem HK-KS xc LDA Construction Challenges Final Remarks
Hartree’s method
Single-particle Schr¨odinger equation
−
2
2m
2
+ vext(r) + vH (r) ϕi(r) = iϕi(r) ,
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 5/76
ENFMC

11. Problem HK-KS xc LDA Construction Challenges Final Remarks
Hartree’s method
Single-particle Schr¨odinger equation
−
2
2m
2
+ vext(r) + vH (r) ϕi(r) = iϕi(r) ,
Mean field potential
vH (r) = e2
d3
r
n(r )
|r − r |
Hartree energy
UH [n] = ΨH | ˆU|ΨH =
e2
2
d3
r d3
r
n(r)n(r )
|r − r |
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 5/76
ENFMC

12. Problem HK-KS xc LDA Construction Challenges Final Remarks
Hartree’s method
Single-particle Schr¨odinger equation
−
2
2m
2
+ vext(r) + vH (r) ϕi(r) = iϕi(r) ,
Mean field potential
vH (r) = e2
d3
r
n(r )
|r − r |
Hartree energy
UH [n] = ΨH | ˆU|ΨH =
e2
2
d3
r d3
r
n(r)n(r )
|r − r |
.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 5/76
ENFMC

13. Problem HK-KS xc LDA Construction Challenges Final Remarks
Hartree-Fock
Antisymmetrization in a Slater determinant
ΨHF (r) =
1
√
N!
ϕ1(x1) ϕ1(x2) · · · ϕ1(xN )
ϕ2(x1) ϕ2(x2) · · · ϕ2(xN )
...
...
...
...
ϕN (x1) ϕN (x2) · · · ϕN (xN )
Fock exchange energy (indirect)
Ex = ΨHF | ˆU|ΨHF = −
e2
2 i,j,σ
dr dr
ϕ∗
iσ(r)ϕ∗
jσ(r )ϕiσ(r )ϕjσ(r)
|r − r |
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 6/76
ENFMC

14. Problem HK-KS xc LDA Construction Challenges Final Remarks
Thomas-Fermi model
Use the infinite gas of non-interacting electrons with a
uniform density n = n(r) to evaluate the kinetic energy of
atoms, molecules
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

15. Problem HK-KS xc LDA Construction Challenges Final Remarks
Thomas-Fermi model
Use the infinite gas of non-interacting electrons with a
uniform density n = n(r) to evaluate the kinetic energy of
atoms, molecules
TTF [n] = tgas(n(r))n(r)d3
r
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

16. Problem HK-KS xc LDA Construction Challenges Final Remarks
Our tutorial
Introduction to density-functional theory
Context and key concepts (1927-1930)
(Born-Oppenheimer, Hartree, Hartree-Fock, Thomas-Fermi)
Fundamentals (1964-1965)
(Hohenberg-Kohn theorem, Kohn-Sham scheme)
Approximations (≈ 1980-2010)
(local density and generalized gradient approximations (LDA and
GGA), construction of functionals)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

17. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to our question
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

18. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to our question
a program ? a method?
some
obscure
theory?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 6/76
ENFMC

19. Problem HK-KS xc LDA Construction Challenges Final Remarks
Density functional theory (DFT)
Quantum theory based on the density n(r)
wave functions Ψ(r1, r2, ...rN )
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

20. Problem HK-KS xc LDA Construction Challenges Final Remarks
Density functional theory (DFT)
Quantum theory based on the density n(r)
wave functions Ψ(r1, r2, ...rN )
Single-particle Kohn-Sham equations
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

21. Problem HK-KS xc LDA Construction Challenges Final Remarks
Density functional theory (DFT)
Quantum theory based on the density n(r)
wave functions Ψ(r1, r2, ...rN )
Single-particle Kohn-Sham equations
Electronic structure boom: Nobel Prize to
W.Kohn/J.Pople
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

22. Problem HK-KS xc LDA Construction Challenges Final Remarks
Density functional theory (DFT)
Quantum theory based on the density n(r)
wave functions Ψ(r1, r2, ...rN )
Single-particle Kohn-Sham equations
Electronic structure boom: Nobel Prize to
W.Kohn/J.Pople
Hohenberg-Kohn theorem: Ψ(r1, r2, ..., rN ) ⇔ n(r)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

23. Problem HK-KS xc LDA Construction Challenges Final Remarks
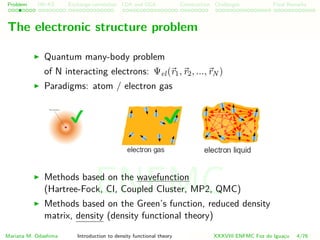
Density functional theory (DFT)
Quantum theory based on the density n(r)
wave functions Ψ(r1, r2, ...rN )
Single-particle Kohn-Sham equations
Electronic structure boom: Nobel Prize to
W.Kohn/J.Pople
Hohenberg-Kohn theorem: Ψ(r1, r2, ..., rN ) ⇔ n(r)
Which means,
Ψ(r) = Ψ[n(r)]
observables = observables[n(r)]
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 7/76
ENFMC

24. Problem HK-KS xc LDA Construction Challenges Final Remarks
Hohenberg-Kohn (1964)
Phys. Rev. 136 B864 (1964).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 8/76
ENFMC

25. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
From the ground-state density it is possible, in principle, to
calculate the corresponding wave functions and all its
observables.
However: the Hohenberg-Kohn theorem does not
provide any means to actually calculate them.
We have DFT in theory, now, in practice?...
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 9/76
ENFMC

26. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
From the ground-state density it is possible, in principle, to
calculate the corresponding wave functions and all its
observables.
However: the Hohenberg-Kohn theorem does not
provide any means to actually calculate them.
We have DFT in theory, now, in practice?...
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 9/76
ENFMC

27. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
arXiv:1403.5164
“By the late fall of 1964, Kohn was thinking about alternative
ways to transform the theory he and Hohenberg had developed
into a practical scheme for atomic, molecular, and solid state
calculations. Happily, he was very well acquainted with an
approximate approach to the many-electron problem that was
notably superior to the Thomas-Fermi method, at least for the
case of atoms. This was a theory proposed by Douglas Hartree in
1923 which exploited the then just-published Schr¨odinger equation
in a heuristic way to calculate the orbital wave functions φk(r), the
electron binding energies k, and the charge density n(r) of an
N-electron atom. Hartree’s theory transcended Thomas-Fermi
theory primarily by its use of the exact quantum-mechanical
expression for the kinetic energy of independent electrons.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 10/76
ENFMC

28. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
Kohn believed the Hartree equations could be an example of
the HK variational principle.
He knew the self-consistent scheme and that it could give an
approximate density
So he suggested to his new post-doc, Lu Sham, that he try to
derive the Hartree equations from the Hohenberg-Kohn
formalism.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 11/76
ENFMC

29. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
Kohn believed the Hartree equations could be an example of
the HK variational principle.
He knew the self-consistent scheme and that it could give an
approximate density
So he suggested to his new post-doc, Lu Sham, that he try to
derive the Hartree equations from the Hohenberg-Kohn
formalism.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 11/76
ENFMC

30. Problem HK-KS xc LDA Construction Challenges Final Remarks
After THK
Kohn believed the Hartree equations could be an example of
the HK variational principle.
He knew the self-consistent scheme and that it could give an
approximate density
So he suggested to his new post-doc, Lu Sham, that he try to
derive the Hartree equations from the Hohenberg-Kohn
formalism.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 11/76
ENFMC

31. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham approach/scheme
Auxiliary non-interacting system
Single-particle equations
−
2 2
2m
+ vKS (r) ϕk(r) = kϕk(r)
Effective potential
vKS (r) = vext(r) + vH (r) + vxc(r)
Formally: constraint on the ground-state density
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 12/76
ENFMC

32. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham kindergarden
Interacting
(complicated)
Ficticious non-interacting
under effective field
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 13/76
ENFMC

33. Problem HK-KS xc LDA Construction Challenges Final Remarks
Outline
1 Review of our problem
2 Review of HK-KS
3 Exchange-correlation
4 LDA and GGA
5 Construction
6 Challenges
7 Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 13/76
ENFMC

34. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 13/76
ENFMC

35. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation
arXiv:1403.5164
“As trained solid-state physicists, Hohenberg and Kohn knew
that the entire history of research on the quantum mechanical
many-electron problem could be interpreted as attempts to
identify and quantify the physical effects described by this
universal density functional.” For example, many years of
approximate quantum mechanical calculations for atoms and
molecules had established that the phenomenon of exchange -
a consequence of the Pauli exclusion principle - contributes
significantly to the potential energy part of U[n]. Exchange
reduces the Coulomb potential energy of the system by tending
to keep electrons with parallel spin spatially separated.”.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 14/76
ENFMC

36. Problem HK-KS xc LDA Construction Challenges Final Remarks
Universal functional
Energy functional: Kinetic + Coulomb + External
E[n] = T[n] + U[n] + V [n]
We can define a universal F[n]
F[n] = T[n] + U[n]
which is the same independent of your system. Our task is
approximate U[n], the many-particle problem.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 15/76
ENFMC

37. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation
arXiv:1403.5164
“As trained solid-state physicists, Hohenberg and Kohn knew
that the entire history of research on the quantum mechanical
many-electron problem could be interpreted as attempts to
identify and quantify the physical effects described by this
universal density functional. For example, many years of
approximate quantum mechanical calculations for atoms and
molecules had established that the phenomenon of exchange -
a consequence of the Pauli exclusion principle - contributes
significantly to the potential energy part of U[n].Exchange
reduces the Coulomb potential energy of the system by tending
to keep electrons with parallel spin spatially separated.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 16/76
ENFMC

38. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation
arXiv:1403.5164
“As trained solid-state physicists, Hohenberg and Kohn knew
that the entire history of research on the quantum mechanical
many-electron problem could be interpreted as attempts to
identify and quantify the physical effects described by this
universal density functional. For example, many years of
approximate quantum mechanical calculations for atoms and
molecules had established that the phenomenon of exchange -
a consequence of the Pauli exclusion principle - contributes
significantly to the potential energy part of U[n]. Exchange
reduces the Coulomb potential energy of the system by tending
to keep electrons with parallel spin spatially separated.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 16/76
ENFMC

39. Problem HK-KS xc LDA Construction Challenges Final Remarks
Coulomb energy
Coulomb energy
U[n] = UH [n] + Ex[n] +
where
UH [n] =
e2
2
d3
r d3
r
n(r)n(r )
|r − r |
.
is the electrostatic, mean field repulsion, and
Ex[ϕ[n]] = −
e2
2 i,j,σ
d3
r d3
r
ϕ∗
iσ(r)ϕ∗
jσ(r )ϕiσ(r )ϕjσ(r)
|r − r |
is the exchange energy due to the Pauli principle.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 17/76
ENFMC

40. Problem HK-KS xc LDA Construction Challenges Final Remarks
Coulomb energy
Coulomb energy
U[n] = UH [n] + Ex[n] +
where
UH [n] =
e2
2
d3
r d3
r
n(r)n(r )
|r − r |
.
is the electrostatic, mean field repulsion, and
Ex[ϕ[n]] = −
e2
2 i,j,σ
d3
r d3
r
ϕ∗
iσ(r)ϕ∗
jσ(r )ϕiσ(r )ϕjσ(r)
|r − r |
is the exchange energy due to the Pauli principle.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 17/76
ENFMC

41. Problem HK-KS xc LDA Construction Challenges Final Remarks
On correlation
arXiv:1403.5164
Coulomb energy
U[n] = UH [n] + Ex[n] +
“The remaining potential energy part of U[n] takes account of
short-range correlation effects.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 18/76
ENFMC

42. Problem HK-KS xc LDA Construction Challenges Final Remarks
On correlation
arXiv:1403.5164
Coulomb energy
U[n] = UH [n] + Ex[n] +
“The remaining potential energy part of U[n] takes account of
short-range correlation effects. Correlation also reduces the
Coulomb potential energy by tending to keep all pairs of
electrons spatially separated.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 18/76
ENFMC

43. Problem HK-KS xc LDA Construction Challenges Final Remarks
On correlation
arXiv:1403.5164
Coulomb energy
U[n] = UH [n] + Ex[n] + Ec[n]
“The remaining potential energy part of U[n] takes account of
short-range correlation effects. Correlation also reduces the
Coulomb potential energy by tending to keep all pairs of
electrons spatially separated.”
Correlation energy: Ec < 0
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 18/76
ENFMC

44. Problem HK-KS xc LDA Construction Challenges Final Remarks
On correlation
arXiv:1403.5164
Coulomb energy
U[n] = UH [n] + Ex[n] + Ec[n]
“Note for future reference that the venerable Hartree-Fock
approximation takes account of the kinetic energy and the
exchange energy exactly but (by definition) takes no account
of the correlation energy”.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 19/76
ENFMC

45. Problem HK-KS xc LDA Construction Challenges Final Remarks
On correlation
arXiv:1403.5164
Coulomb energy
U[n] = UH [n] + Ex[n] + Ec[n]
“Note for future reference that the venerable Hartree-Fock
approximation takes account of the kinetic energy and the
exchange energy exactly but (by definition) takes no account
of the correlation energy”.
Hartree-Fock energy
EHF
[n] = Ts[ϕ[n]] + V [n] + UH [n] + Ex[ϕ[n]]
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 19/76
ENFMC

46. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation in DFT
Kohn-Sham effective potential:
vKS (r) = vext(r) + vH (r) + vxc(r)
Our task is to find vxc, preferrably as a functional of the density.
Orbital functionals bring non-locality (integrals over r and r ).
So, in the Kohn-Sham DFT, we recast the many-particle problem
in finding xc potentials.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 20/76
ENFMC

47. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation in DFT
Total energy
E[n] = T[n] + V [n] + U[n]
= Ts[ϕi[n]] + V [n] + UH [n] + Exc[n]
Some approximations: single-particle kinetic and Hartree.
Leave the corrections (T − Ts and U − UH ) to the Exc.
Ts[ϕi[n]] = −
2
2m
N
i
d3
rϕ∗
i (r) 2
ϕi(r)
UH [n] =
e2
2
d3
r d3
r
n(r)n(r )
| r − r |
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 21/76
ENFMC

48. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation energy
The exchange-correlation energy Exc is the new clothing of the
many-body problem
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 22/76
ENFMC

49. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation energy
The exchange-correlation energy Exc is the new clothing of the
many-body problem
exchange: Pauli principle
correlation: kinetic and Coulombic contributions beyond
single-particle (one Slater determinant)
xc = “nature’s glue” that binds matter together (Exc < 0)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 22/76
ENFMC

50. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation energy
“Electrons moving through the density
swerve to avoid one another, like shoppers
in a mall.”
“The resulting reduction of the potential energy of mutual
Coulomb repulsion is the main contribution to the negative
exchange-correlation energy. The swerving motion also makes a
small positive kinetic energy contribution to the correlation energy”
J.Perdew et al. in J. Chem. Theory Comput. 5, 902 (2009).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 23/76
ENFMC

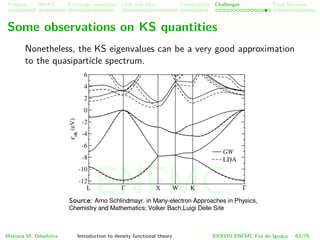
51. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation energy
In Kohn-Sham DFT, the exchange-correlation energy Exc[n] holds
the main difficulty of the many-body problem.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 24/76
ENFMC

52. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange-correlation energy
In Kohn-Sham DFT, the exchange-correlation energy Exc[n] holds
the main difficulty of the many-body problem.
Now, how to construct an approximate Exc[n]?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 24/76
ENFMC

53. Problem HK-KS xc LDA Construction Challenges Final Remarks
Outline
1 Review of our problem
2 Review of HK-KS
3 Exchange-correlation
4 LDA and GGA
5 Construction
6 Challenges
7 Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 24/76
ENFMC

54. Problem HK-KS xc LDA Construction Challenges Final Remarks
State-of-the-art
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 25/76
ENFMC

55. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back in 65
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 26/76
ENFMC

56. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back in 65
Introduce KS equations
Explore possible Exc
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 27/76
ENFMC

57. Problem HK-KS xc LDA Construction Challenges Final Remarks
Density functional
Starting point: electron gas
Exc = d3
rexc[n]n(r) (exc: energy density per particle)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 28/76
ENFMC

58. Problem HK-KS xc LDA Construction Challenges Final Remarks
Thomas-Fermi-Dirac spirit
Using the paradigm of an uniform, homogeneous system to
help with inhomogeneous problems
E ≈ ETFD
[n] = TLDA
s [n] + UH [n] + ELDA
x + V [n] .
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 29/76
ENFMC

59. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

60. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

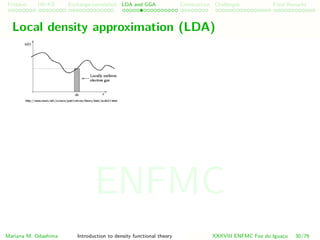
61. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
ELDA
xc [n] = d3
r ehom
xc (n(r))
ehom
xc (n) = ehom
x (n) + ehom
c (n)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

62. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
ELDA
xc [n] = d3
r ehom
xc (n(r))
ehom
xc (n) = ehom
x (n) + ehom
c (n)
For the homogeneous electron gas, we have the expression of the
Dirac exchange energy
ehom
x (n) = −
3
4
3
π
1/3
n4/3
,
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

63. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
ELDA
xc [n] = d3
r ehom
xc (n(r))
ehom
xc (n) = ehom
x (n) + ehom
c (n)
For the homogeneous electron gas, we have the expression of the
Dirac exchange energy
ehom
x (n) = −
3
4
3
π
1/3
n4/3
,
For ehom
c ?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

64. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
ELDA
xc [n] = d3
r ehom
xc (n(r))
ehom
xc (n) = ehom
x (n) + ehom
c (n)
For the homogeneous electron gas, we have the expression of the
Dirac exchange energy
ehom
x (n) = −
3
4
3
π
1/3
n4/3
,
For ehom
c ? Monte Carlo Quˆantico → parametrizations
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

65. Problem HK-KS xc LDA Construction Challenges Final Remarks
Local density approximation (LDA)
ELDA
xc [n] = d3
r ehom
xc (n(r))
ehom
xc (n) = ehom
x (n) + ehom
c (n)
For the homogeneous electron gas, we have the expression of the
Dirac exchange energy
ehom
x (n) = −
3
4
3
π
1/3
n4/3
,
For ehom
c ? Monte Carlo Quˆantico → parametrizations
ePW92
c = −2c0(1+α1rs)ln 1 +
1
2c1(β1r
1/2
s + β2rs + β3r
3/2
s + β4r2
s )
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 30/76
ENFMC

66. Problem HK-KS xc LDA Construction Challenges Final Remarks
Parametrizations of the correlation energy
E.g.: low-density limit of the electron gas
ec(rs) = −e2 d0
rs
+
d1
r
3/2
s
+
d2
r4
s
+ ... rs → ∞ ,
Wigner’s parametrization (1934):
eW
c (rs) = −
0.44e2
7.8 + rs
.
W (Wigner-1934)
BR (Brual Rothstein-1978)
vBH (von Barth e
Hedin-1972)
GL (Gunnarson e
Lundqvist-1976)
VWN (Vosko, Wilk e
Nusair-1980)
PZ (Perdew e Zunger-1981)
PW92 (Perdew e
Wang-1992)
EHTY (Endo et al-1999)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 31/76
ENFMC

67. Problem HK-KS xc LDA Construction Challenges Final Remarks
Next step: Inhomogeneities, gradient of the density
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 32/76
ENFMC

68. Problem HK-KS xc LDA Construction Challenges Final Remarks
Gradient expansion approximation (GEA)
Systematic corrections to LDA for slowly varying densities
Inhomogeneities captured by “reduced density gradients”
Ex[n] = Ax d3
r n4/3
[1+µs2
+...]
Ec[n] = d3
r n[ec(n)+β(n)t2
+...]
where s =
| n|
2kF n
e t =
| n|
2ksn
Truncated expansion leads to violation of sum rules
For atoms, exchange improves over LDA, but not correlation (gets
even positive)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 33/76
ENFMC

69. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

70. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

71. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Langreth e Mehl (1983): random-phase approximation helps corrections;
correlation cutoff; semiempirical
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

72. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Langreth e Mehl (1983): random-phase approximation helps corrections;
correlation cutoff; semiempirical
Perdew e Wang (PW86): LM83 extended without empiricism, lower
exchange errors of LDA to 1-10%
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

73. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Langreth e Mehl (1983): random-phase approximation helps corrections;
correlation cutoff; semiempirical
Perdew e Wang (PW86): LM83 extended without empiricism, lower
exchange errors of LDA to 1-10%
Becke (B88): correct assintotic behavior of exchange energy; fitted
parameter from atomic energies
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

74. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Langreth e Mehl (1983): random-phase approximation helps corrections;
correlation cutoff; semiempirical
Perdew e Wang (PW86): LM83 extended without empiricism, lower
exchange errors of LDA to 1-10%
Becke (B88): correct assintotic behavior of exchange energy; fitted
parameter from atomic energies
PW91: same Becke’s Fxc idea, impose correlation cutoff, and a good
parametrization of correlation (PW92). Attempts to obey as many
universal constraints as possible. No empirical parameters.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

75. Problem HK-KS xc LDA Construction Challenges Final Remarks
Generalized gradient approximation (GGA)
GEA successor; widened the applications of DFT in quantum
chemistry
EGGA
xc [n] = d3
r f (n(r), n(r))
Ma e Brueckner (1968): first GGA, empirical parameter corrects positive
correlation energies
Langreth e Mehl (1983): random-phase approximation helps corrections;
correlation cutoff; semiempirical
Perdew e Wang (PW86): LM83 extended without empiricism, lower
exchange errors of LDA to 1-10%
Becke (B88): correct assintotic behavior of exchange energy; fitted
parameter from atomic energies
PW91: same Becke’s Fxc idea, impose correlation cutoff, and a good
parametrization of correlation (PW92). Attempts to obey as many
universal constraints as possible. No empirical parameters.
PBE GGA was announced as “GGA made simple”, PW91 substitute
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 34/76
ENFMC

76. Problem HK-KS xc LDA Construction Challenges Final Remarks
State-of-the-art
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 35/76
ENFMC

77. Problem HK-KS xc LDA Construction Challenges Final Remarks
Perdew-Burke-Ernzerhof GGA (1996)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 36/76
ENFMC

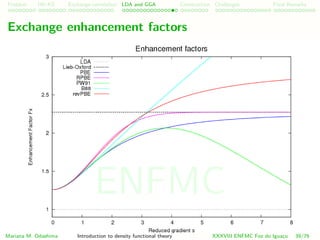
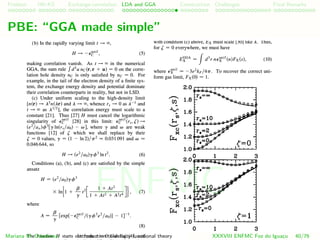
78. Problem HK-KS xc LDA Construction Challenges Final Remarks
Visualizing GGAs non-locality
Enhancement factor Fxc:
EGGA
xc [n] ≈ d3
r n Fxc(rs, ζ, s) ex(rs, ζ = 0)
Captures the effects of
correlation (through rs)
spin polarization (ζ)
density inhomogeneity (through the reduced density gradient s).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 37/76
ENFMC

79. Problem HK-KS xc LDA Construction Challenges Final Remarks
Example: PBE exchange
FPBE
x (s) = 1 + κ −
κ
1 + µ
κ s2
,
µ = π2
βGE
/3, so that there will be a cancellation of the exchange
and correlation gradients, and the jellium result is recovered.
βGE
comes from the second-order gradient expansion in the limit of
slowly-varying densities
κ is fixed by the Lieb-Oxford bound
s is the “reduced density gradient”
s =
| n|
2(3π2)1/3n4/3
=
| n|
2kF n
,
which corresponds to a inhomogeneity parameter, measuring how fast the
density changes in the scale of the Fermi wavelength 2π/kF .
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 38/76
ENFMC

80. Problem HK-KS xc LDA Construction Challenges Final Remarks
Exchange enhancement factors
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 39/76
ENFMC

81. Problem HK-KS xc LDA Construction Challenges Final Remarks
PBE: “GGA made simple”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 40/76
ENFMC

82. Problem HK-KS xc LDA Construction Challenges Final Remarks
Outline
1 Review of our problem
2 Review of HK-KS
3 Exchange-correlation
4 LDA and GGA
5 Construction
6 Challenges
7 Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 40/76
ENFMC

83. Problem HK-KS xc LDA Construction Challenges Final Remarks
Two construction approaches
Fitting empirical parameters
E.g.: B3LYP (A. Becke on the right)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 41/76
ENFMC

84. Problem HK-KS xc LDA Construction Challenges Final Remarks
Two construction approaches
Fitting empirical parameters
E.g.: B3LYP (A. Becke on the right)
Inserting exact constraints (↔ J. Perdew)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 41/76
ENFMC

85. Problem HK-KS xc LDA Construction Challenges Final Remarks
Two construction approaches
Fitting empirical parameters
E.g.: B3LYP (A. Becke on the right)
Inserting exact constraints (↔ J. Perdew)
n = uniform → LDA
n ≈ uniform → LDA + O( ) = GEA
Ex < 0, Ec 0
Uniform density scaling
Spin scaling
One-electron limit
Derivative discontinuity
Lower bounds
Ex.: PW86, PW91, PBE
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 41/76
ENFMC

86. Problem HK-KS xc LDA Construction Challenges Final Remarks
Constraint satisfaction
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 42/76
ENFMC

87. Problem HK-KS xc LDA Construction Challenges Final Remarks
Constraint satisfaction
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 43/76
ENFMC

88. Problem HK-KS xc LDA Construction Challenges Final Remarks
State-of-the-art
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 44/76
ENFMC

89. Problem HK-KS xc LDA Construction Challenges Final Remarks
State-of-the-art
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 44/76
ENFMC

90. Problem HK-KS xc LDA Construction Challenges Final Remarks
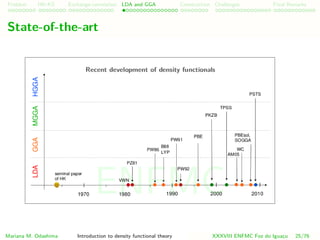
Beyond LDA and GGA
Meta-GGA: + non-interacting kinetic energy density τ. Ex: TPSS, PKZB
EMGGA
xc [n] = d3
rf (n(r), n(r), τ[n])
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 45/76
ENFMC

91. Problem HK-KS xc LDA Construction Challenges Final Remarks
Beyond LDA and GGA
Meta-GGA: + non-interacting kinetic energy density τ. Ex: TPSS, PKZB
EMGGA
xc [n] = d3
rf (n(r), n(r), τ[n])
Hiper-GGA: + exact exchange energy density ex
EHGGA
xc [n] = d3
rf (n(r), n(r), τ[n], ex[n]) ,
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 45/76
ENFMC

92. Problem HK-KS xc LDA Construction Challenges Final Remarks
Beyond LDA and GGA
Meta-GGA: + non-interacting kinetic energy density τ. Ex: TPSS, PKZB
EMGGA
xc [n] = d3
rf (n(r), n(r), τ[n])
Hiper-GGA: + exact exchange energy density ex
EHGGA
xc [n] = d3
rf (n(r), n(r), τ[n], ex[n]) ,
Hybrids: mix of exact exchange Ex with ELDA
x and Eaprox
c . Ex: B3LYP
Ehib
xc [n] = aEexact
x + (1 − a)ELDA
x [n] + Eaprox
c
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 45/76
ENFMC

93. Problem HK-KS xc LDA Construction Challenges Final Remarks
Beyond LDA and GGA functionals
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 46/76
ENFMC

94. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic improvement?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 47/76
ENFMC

95. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic improvement?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 47/76
ENFMC

96. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic trends?
Consider
Localized vs extended densities; covalent and ionic bonds
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

97. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic trends?
Consider
Localized vs extended densities; covalent and ionic bonds
Systematic trends between LDA e PBE; between GGAs e
hybrids
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

98. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic trends?
Consider
Localized vs extended densities; covalent and ionic bonds
Systematic trends between LDA e PBE; between GGAs e
hybrids
Example: lattice constants
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

99. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic trends?
Consider
Localized vs extended densities; covalent and ionic bonds
Systematic trends between LDA e PBE; between GGAs e
hybrids
Example: lattice constants
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

100. Problem HK-KS xc LDA Construction Challenges Final Remarks
Systematic trends?
Consider
Localized vs extended densities; covalent and ionic bonds
Systematic trends between LDA e PBE; between GGAs e
hybrids
Example: lattice constants
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

101. Problem HK-KS xc LDA Construction Challenges Final Remarks
Outline
1 Review of our problem
2 Review of HK-KS
3 Exchange-correlation
4 LDA and GGA
5 Construction
6 Challenges
7 Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 48/76
ENFMC

102. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT downsides
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 49/76
ENFMC

103. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT downsides
DFT is variational, not perturbative: no systematic
improvement
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 49/76
ENFMC

104. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT downsides
DFT is variational, not perturbative: no systematic
improvement
Kohn-Sham quantities lack physical meaning
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 49/76
ENFMC

105. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT downsides
DFT is variational, not perturbative: no systematic
improvement
Kohn-Sham quantities lack physical meaning
In principle, everything can be extracted from the density;
however, there is no prescription for building the HK or xc
density functional
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 49/76
ENFMC

106. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFA downsides (density-functional approximations)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 50/76
ENFMC

107. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFA downsides (density-functional approximations)
No prescription for building the xc density functional
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 50/76
ENFMC

108. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFA downsides (density-functional approximations)
No prescription for building the xc density functional
Combining exact constraints: arbitrary forms
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 50/76
ENFMC

109. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFA downsides (density-functional approximations)
No prescription for building the xc density functional
Combining exact constraints: arbitrary forms
Single-particle and electron gas paradigm may not be
enough
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 50/76
ENFMC

110. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFA downsides (density-functional approximations)
No prescription for building the xc density functional
Combining exact constraints: arbitrary forms
Single-particle and electron gas paradigm may not be
enough
Often we miss the condensed-matter richness: strong
correlations, excitations, dispersion forces, relativistic
effects
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 50/76
ENFMC

111. Problem HK-KS xc LDA Construction Challenges Final Remarks
What typical functionals miss
Strong correlations
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 51/76
ENFMC

112. Problem HK-KS xc LDA Construction Challenges Final Remarks
What typical functionals miss
Strong correlations
Dispersion forces
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 51/76
ENFMC

113. Problem HK-KS xc LDA Construction Challenges Final Remarks
What typical functionals miss
Strong correlations
Dispersion forces
Band gaps
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 51/76
ENFMC

114. Problem HK-KS xc LDA Construction Challenges Final Remarks
What typical functionals miss
Strong correlations
Dispersion forces
Band gaps Charge-transfer
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 51/76
ENFMC

115. Problem HK-KS xc LDA Construction Challenges Final Remarks
What is wrong in our approximations?
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 52/76
ENFMC

116. Problem HK-KS xc LDA Construction Challenges Final Remarks
There are different problems that arise in common density
functional approximations.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 53/76
ENFMC

117. Problem HK-KS xc LDA Construction Challenges Final Remarks
There are different problems that arise in common density
functional approximations.
I will quickly comment two of them.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 53/76
ENFMC

118. Problem HK-KS xc LDA Construction Challenges Final Remarks
There are different problems that arise in common density
functional approximations.
I will quickly comment two of them.
Self-interaction error and delocalization error
Derivative discontinuity
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 53/76
ENFMC

119. Problem HK-KS xc LDA Construction Challenges Final Remarks
Self-interaction error
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 54/76
ENFMC

120. Problem HK-KS xc LDA Construction Challenges Final Remarks
Self-interaction error
Take your functional and evaluate it for a one-electron density.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 54/76
ENFMC

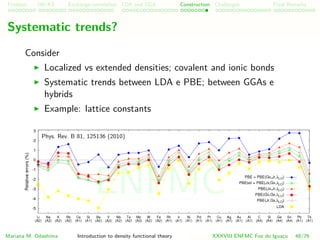
121. Problem HK-KS xc LDA Construction Challenges Final Remarks
Self-interaction error
Take your functional and evaluate it for a one-electron density.
In principle, if you have one electron, there is no Coulomb
interaction and you should have
U[n(1)
] = 0
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 54/76
ENFMC

122. Problem HK-KS xc LDA Construction Challenges Final Remarks
Self-interaction error
Take your functional and evaluate it for a one-electron density.
In principle, if you have one electron, there is no Coulomb
interaction and you should have
U[n(1)
] = 0
this means that
UH [n(1)
] + Ex[n(1)
] + Ec[n(1)
] = 0
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 54/76
ENFMC

123. Problem HK-KS xc LDA Construction Challenges Final Remarks
Self-interaction error
Take your functional and evaluate it for a one-electron density.
In principle, if you have one electron, there is no Coulomb
interaction and you should have
U[n(1)
] = 0
this means that
UH [n(1)
] + Ex[n(1)
] + Ec[n(1)
] = 0
However, many common functionals have a spurious error, called
self-interaction, leaving a small amount of extra charge. This is a
problem that affects strongly correlated systems.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 54/76
ENFMC

124. Problem HK-KS xc LDA Construction Challenges Final Remarks
Delocalization error
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 55/76
ENFMC

125. Problem HK-KS xc LDA Construction Challenges Final Remarks
Delocalization error
Consider a system of N electrons.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 55/76
ENFMC

126. Problem HK-KS xc LDA Construction Challenges Final Remarks
Delocalization error
Consider a system of N electrons.
If I add or remove one electron, it was proved [Perdew et al 1982]
that the total energy behaves linearly with N:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 55/76
ENFMC

127. Problem HK-KS xc LDA Construction Challenges Final Remarks
Delocalization error
Consider a system of N electrons.
If I add or remove one electron, it was proved [Perdew et al 1982]
that the total energy behaves linearly with N:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 55/76
ENFMC

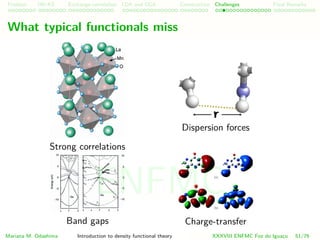
128. Problem HK-KS xc LDA Construction Challenges Final Remarks
Delocalization error
Consider a system of N electrons.
If I add or remove one electron, it was proved [Perdew et al 1982]
that the total energy behaves linearly with N:
However, common density functionals behave concavely,
sometimes favoring fractional configurations. This affects problems
of charge transfer in molecules or electronic transport.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 55/76
ENFMC

129. Problem HK-KS xc LDA Construction Challenges Final Remarks
There are several illnesses that arise from the KS picture and
common density functional approximations.
I will quickly comment two of them.
Self-interaction error and delocalization error
Derivative discontinuity
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 56/76
ENFMC

130. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity (I)
As we observed, the derivative of energy changes discontinuosly
when we change the particle number:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 57/76
ENFMC

131. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity (I)
As we observed, the derivative of energy changes discontinuosly
when we change the particle number:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 57/76
ENFMC

132. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity (I)
As we observed, the derivative of energy changes discontinuosly
when we change the particle number:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 57/76
ENFMC

133. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity and the fundamental gap
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 58/76
ENFMC

134. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity and the fundamental gap
The fundamental gap in solid-state physics (photoemission gap, 2x
chemical hardness) is defined by
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 58/76
ENFMC

135. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity and the fundamental gap
The fundamental gap in solid-state physics (photoemission gap, 2x
chemical hardness) is defined by
Fundamental gap: Ionization potential - Electron affinity
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 58/76
ENFMC

136. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity and the fundamental gap
The fundamental gap in solid-state physics (photoemission gap, 2x
chemical hardness) is defined by
Fundamental gap: Ionization potential - Electron affinity
Ionization potential:
I = E(N−1)−E(N) = −
∂E
∂N N−δN
Electron affinity:
A = E(N)−E(N+1) = −
∂E
∂N N+δN
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 58/76
ENFMC

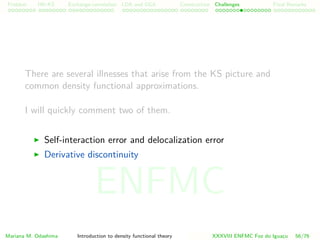
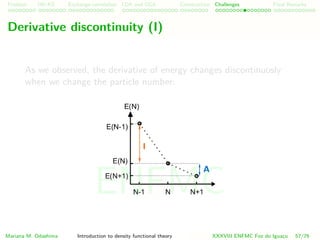
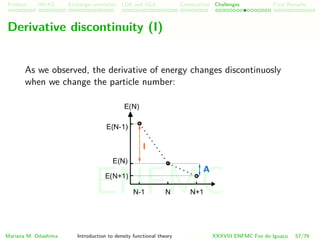
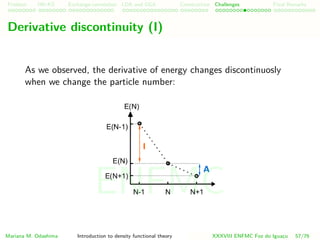
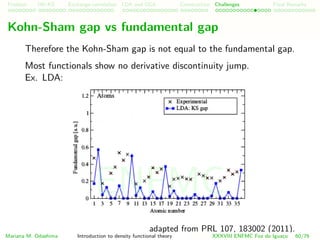
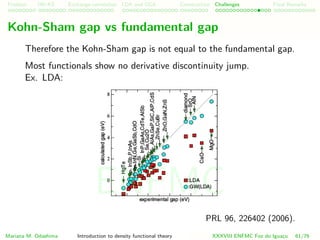
137. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity in our energy functional
In our density functional, the discontinuity will also appear
E[n] = Ts[n] + UH [n] + V [n] + Exc[n]
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 59/76
ENFMC

138. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity in our energy functional
In our density functional, the discontinuity will also appear
E[n] = Ts[n] + UH [n] + V [n] + Exc[n]
The discontinuous kinetic part is called Kohn-Sham non-interacing
gap, and the xc part is the derivative discontinuity, the many-body
correction to the Kohn-Sham non-interacting gap.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 59/76
ENFMC

139. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity in our energy functional
In our density functional, the discontinuity will also appear
E[n] = Ts[n] + UH [n] + V [n] + Exc[n]
The discontinuous kinetic part is called Kohn-Sham non-interacing
gap, and the xc part is the derivative discontinuity, the many-body
correction to the Kohn-Sham non-interacting gap.
∆L =
δExc[n]
δn(r) N+δN
−
δExc[n]
δn(r) N−δN
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 59/76
ENFMC

140. Problem HK-KS xc LDA Construction Challenges Final Remarks
Derivative discontinuity in our energy functional
In our density functional, the discontinuity will also appear
E[n] = Ts[n] + UH [n] + V [n] + Exc[n]
The discontinuous kinetic part is called Kohn-Sham non-interacing
gap, and the xc part is the derivative discontinuity, the many-body
correction to the Kohn-Sham non-interacting gap.
∆L =
δExc[n]
δn(r) N+δN
−
δExc[n]
δn(r) N−δN
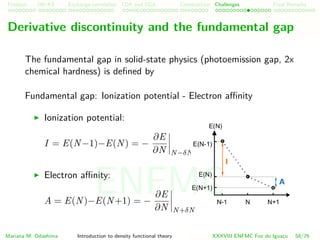
The fundamental gap (I-A) is given by the sum
∆fund = ∆KS + ∆L
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 59/76
ENFMC

141. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham gap vs fundamental gap
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 60/76
ENFMC

142. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham gap vs fundamental gap
Therefore the Kohn-Sham gap is not equal to the fundamental gap.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 60/76
ENFMC

143. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham gap vs fundamental gap
Therefore the Kohn-Sham gap is not equal to the fundamental gap.
Most functionals show no derivative discontinuity jump.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 60/76
ENFMC

144. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham gap vs fundamental gap
Therefore the Kohn-Sham gap is not equal to the fundamental gap.
Most functionals show no derivative discontinuity jump.
Ex. LDA:
adapted from PRL 107, 183002 (2011).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 60/76
ENFMC

145. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn-Sham gap vs fundamental gap
Therefore the Kohn-Sham gap is not equal to the fundamental gap.
Most functionals show no derivative discontinuity jump.
Ex. LDA:
PRL 96, 226402 (2006).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 61/76
ENFMC

146. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 62/76
ENFMC

147. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
The price for the simplification of the problem is that Kohn-Sham
is an auxiliary tool.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 62/76
ENFMC

148. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
The price for the simplification of the problem is that Kohn-Sham
is an auxiliary tool.
The KS mapping gives you the energy and ground-state density.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 62/76
ENFMC

149. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
The price for the simplification of the problem is that Kohn-Sham
is an auxiliary tool.
The KS mapping gives you the energy and ground-state density.
There is no proof that the KS quantities have a physical meaning,
with few exceptions.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 62/76
ENFMC

150. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
The price for the simplification of the problem is that Kohn-Sham
is an auxiliary tool.
The KS mapping gives you the energy and ground-state density.
There is no proof that the KS quantities have a physical meaning,
with few exceptions.
The KS gap is not equal to the fundamental gap, and the
eigenvalues are not quasiparticle spectra.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 62/76
ENFMC

151. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 63/76
ENFMC

152. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
Nonetheless, the KS eigenvalues can be a very good approximation
to the quasiparticle spectrum.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 63/76
ENFMC

153. Problem HK-KS xc LDA Construction Challenges Final Remarks
Some observations on KS quantities
Nonetheless, the KS eigenvalues can be a very good approximation
to the quasiparticle spectrum.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 63/76
ENFMC

154. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

155. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Functionals families (LDA,GGA,MGGA,hybrids):
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

156. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Functionals families (LDA,GGA,MGGA,hybrids):
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

157. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Functionals families (LDA,GGA,MGGA,hybrids):
Important to know the functional proposal and its
improvements
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

158. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Functionals families (LDA,GGA,MGGA,hybrids):
Important to know the functional proposal and its
improvements
Check previous literature on the atomic, bulk trends, their
character and problems
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

159. Problem HK-KS xc LDA Construction Challenges Final Remarks
General recommendations
Functionals families (LDA,GGA,MGGA,hybrids):
Important to know the functional proposal and its
improvements
Check previous literature on the atomic, bulk trends, their
character and problems
When possible, confrontation with experimental or highly
accurate methods
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

160. Problem HK-KS xc LDA Construction Challenges Final Remarks
Outline
1 Review of our problem
2 Review of HK-KS
3 Exchange-correlation
4 LDA and GGA
5 Construction
6 Challenges
7 Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 64/76
ENFMC

161. Problem HK-KS xc LDA Construction Challenges Final Remarks
Timeline
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 65/76
ENFMC

162. Problem HK-KS xc LDA Construction Challenges Final Remarks
Timeline
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 65/76
ENFMC

163. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT Impact
Citation Statistics from 110 Years of Physical Review (1893 - 2003)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 66/76
ENFMC

164. Problem HK-KS xc LDA Construction Challenges Final Remarks
DFT Impact
Citation Statistics from 110 Years of Physical Review (1893 - 2003)
(Physics Today, p.49 Junho 2005)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 66/76
ENFMC

165. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to the electronic structure spirit
“Where solid-state physics has
Fermi energy, chemical potential,
band gap, density of states, and
local density of states, quantum
chemistry has ionization potential,
electron affinity, hardness, softness,
and local softness. Much more too.
DFT is a single language that covers
atoms, molecules, clusters, surfaces,
and solids.”
Robert Parr
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 67/76
ENFMC

166. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to the electronic structure spirit
“Where solid-state physics has
Fermi energy, chemical potential,
band gap, density of states, and
local density of states, quantum
chemistry has ionization potential,
electron affinity, hardness, softness,
and local softness. Much more too.
DFT is a single language that covers
atoms, molecules, clusters, surfaces,
and solids.”
Robert Parr
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 67/76
ENFMC

167. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to the electronic structure spirit
“Where solid-state physics has
Fermi energy, chemical potential,
band gap, density of states, and
local density of states, quantum
chemistry has ionization potential,
electron affinity, hardness, softness,
and local softness. Much more too.
DFT is a single language that covers
atoms, molecules, clusters, surfaces,
and solids.”
Robert Parr
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 67/76
ENFMC

168. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to the electronic structure spirit
“Where solid-state physics has
Fermi energy, chemical potential,
band gap, density of states, and
local density of states, quantum
chemistry has ionization potential,
electron affinity, hardness, softness,
and local softness. Much more too.
DFT is a single language that covers
atoms, molecules, clusters, surfaces,
and solids.”
Robert Parr
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 67/76
ENFMC

169. Problem HK-KS xc LDA Construction Challenges Final Remarks
Back to the electronic structure spirit
“Where solid-state physics has
Fermi energy, chemical potential,
band gap, density of states, and
local density of states, quantum
chemistry has ionization potential,
electron affinity, hardness, softness,
and local softness. Much more too.
DFT is a single language that covers
atoms, molecules, clusters, surfaces,
and solids.”
Robert Parr
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 67/76
ENFMC

170. Problem HK-KS xc LDA Construction Challenges Final Remarks
1964/65-2015
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 68/76
ENFMC

171. Problem HK-KS xc LDA Construction Challenges Final Remarks
1964/65-2015
Hohenberg-Kohn ’64:
Kohn-Sham ’65:
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 68/76
ENFMC

172. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

173. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

174. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

175. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

176. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
In Canadian camps, supported by Red Cross, studies math
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

177. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
In Canadian camps, supported by Red Cross, studies math
Working as lumberjacks, earning 20 cents per day, buys
Slater’s book “Chemical Physics”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

178. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
In Canadian camps, supported by Red Cross, studies math
Working as lumberjacks, earning 20 cents per day, buys
Slater’s book “Chemical Physics”
Joins the Canadian army and gets a BS degree in Applied
Mathematics
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

179. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
In Canadian camps, supported by Red Cross, studies math
Working as lumberjacks, earning 20 cents per day, buys
Slater’s book “Chemical Physics”
Joins the Canadian army and gets a BS degree in Applied
Mathematics
Finishes a crash master’s course and applies for PhDs
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

180. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn
Born in 1923, in a jew middle-class family
World War II: fled to England with help of
family friends -wishing to become a farmer
First interned in British camps for “enemy
aliens”
In Canadian camps, supported by Red Cross, studies math
Working as lumberjacks, earning 20 cents per day, buys
Slater’s book “Chemical Physics”
Joins the Canadian army and gets a BS degree in Applied
Mathematics
Finishes a crash master’s course and applies for PhDs
Awarded a scholarship for Harvard; becomes PhD student of
Julian Schwinger
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 69/76
ENFMC

181. Problem HK-KS xc LDA Construction Challenges Final Remarks
Walter Kohn and Julian Schwinger
Kohn met Schwinger only “a few times a year”.
“It was during these meetings, sometimes
more than 2 hours long, that I learned the
most from him. (...) to dig for the essential;
to pay attention to the experimental facts;
to try to say something precise and operati-
onally meaningful, even if one cannot calcu-
late everything a priori; not to be satisfied un-
til one has embedded his ideas in a coherent,
logical, and aesthetically satisfying structure.
(...) I cannot even imagine my subsequent sci-
entific life without Julian’s example and tea-
ching.”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 70/76
ENFMC

182. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

183. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

184. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

185. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Bell Labs: semiconductor physics (transistor rush)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

186. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Bell Labs: semiconductor physics (transistor rush)
Luttinger; effective mass equation for the energy levels of
impurity states in Silicon: “one-particle method”
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

187. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Bell Labs: semiconductor physics (transistor rush)
Luttinger; effective mass equation for the energy levels of
impurity states in Silicon: “one-particle method”
... electronic transport; phonons; insulating state;
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

188. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Bell Labs: semiconductor physics (transistor rush)
Luttinger; effective mass equation for the energy levels of
impurity states in Silicon: “one-particle method”
... electronic transport; phonons; insulating state;
Mott: Thomas-Fermi for screening
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

189. Problem HK-KS xc LDA Construction Challenges Final Remarks
Kohn’s scientific background
Schwinger: Green’s functions, variational principles, scattering
Van Vleck: entered solid-state physics
Rostocker: Green’s functions to solve the electron band
structure problem (KKR)
Bell Labs: semiconductor physics (transistor rush)
Luttinger; effective mass equation for the energy levels of
impurity states in Silicon: “one-particle method”
... electronic transport; phonons; insulating state;
Mott: Thomas-Fermi for screening
de Gennes, Friedel: metals and alloys;
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 71/76
ENFMC

190. Problem HK-KS xc LDA Construction Challenges Final Remarks
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

191. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

192. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...) are all most notable for
their clarity and the simplicity of the mathematics one
encounters.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

193. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...) are all most notable for
their clarity and the simplicity of the mathematics one
encounters. On many occasions, after reading through
the material, I found myself saying something like “of
course things go that way, I could have written this
myself”. (...)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

194. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...) are all most notable for
their clarity and the simplicity of the mathematics one
encounters. On many occasions, after reading through
the material, I found myself saying something like “of
course things go that way, I could have written this
myself”. (...) It is the case that the most important
and fundamental new ideas and concepts in our field
are very simple and obvious, once they have been set
forth for the first time.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

195. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...) are all most notable for
their clarity and the simplicity of the mathematics one
encounters. On many occasions, after reading through
the material, I found myself saying something like “of
course things go that way, I could have written this
myself”. (...) It is the case that the most important
and fundamental new ideas and concepts in our field
are very simple and obvious, once they have been set
forth for the first time. I am reminded of remarks I
have read recently in an essay by Steven Weinberg,
who states that the very important and fundamental
papers in physics are notable for their clarity.
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

196. Problem HK-KS xc LDA Construction Challenges Final Remarks
“Kohn’s seminal papers (...) are all most notable for
their clarity and the simplicity of the mathematics one
encounters. On many occasions, after reading through
the material, I found myself saying something like “of
course things go that way, I could have written this
myself”. (...) It is the case that the most important
and fundamental new ideas and concepts in our field
are very simple and obvious, once they have been set
forth for the first time. I am reminded of remarks I
have read recently in an essay by Steven Weinberg,
who states that the very important and fundamental
papers in physics are notable for their clarity. The new
ideas are applied quickly because of this.”
Douglas L. Mills
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 72/76
ENFMC

197. Problem HK-KS xc LDA Construction Challenges Final Remarks
Acknowledgements (I)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 73/76
ENFMC

198. Problem HK-KS xc LDA Construction Challenges Final Remarks
Acknowledgements (I)
Klaus Capelle, UFABC, Brazil
E.K.U. Gross, MPI-Halle,Germany
Sam Trickey, QTP-Univ.Florida
Caio Lewenkopf, UFF, Brazil
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 73/76
ENFMC

199. Problem HK-KS xc LDA Construction Challenges Final Remarks
References
Kohn’s Nobel lecture, Electronic structure of matter—wave functions and
density functionals, (http://www.nobelprize.org/nobel_prizes/chemistry/
laureates/1998/kohn-lecture.html)
A. Becke, Perspective: Fifty years of density-functional theory in chemical
physics, (http://www.ncbi.nlm.nih.gov/pubmed/24832308)
K. Capelle, A bird’s-eye view of density-functional theory,
(http://www.scielo.br/scielo.php?script=sci_arttext&pid=
S0103-97332006000700035)
Perdew and Kurth, A Primer in Density Functional Theory,
(http://www.physics.udel.edu/˜bnikolic/QTTG/NOTES/DFT/BOOK=primer_
dft.pdf)
Perdew et al., Some Fundamental Issues in Ground-State Density Functional
Theory: A Guide for the Perplexed
http://pubs.acs.org/doi/full/10.1021/ct800531s
Zangwill, The education of Walter Kohn and the creation of density functional
theory, (http://arxiv.org/abs/1403.5164)
M. M. Odashima, PHD Thesis
(http://www.teses.usp.br/teses/disponiveis/76/76131/tde-14062010-
164125/pt-br.php)
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 74/76
ENFMC

200. Problem HK-KS xc LDA Construction Challenges Final Remarks
References
Electronic Structure Basic - Theory and Practical Methods. Richard M Martin,
Cambridge (2008)
Atomic and Electronic Structure of Solids. Efthimios Kaxiras, Cambridge
(2003).
Density Functional Theory - An Advanced Course. Eberhard Engel and Reiner
M. Dreizler, Springer (2011).
Many-Electron Approaches in Physics, Chemistry and Mathematics: A
Multidisciplinary View. Eds. Volker Bach, Luigi Delle Site, Springer (2014).
Many-Body Approach to Electronic Excitations - Concepts and Applications.
Friedhelm Bechstedt, Springer (2015).
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 75/76
ENFMC

201. Problem HK-KS xc LDA Construction Challenges Final Remarks
Acknowledgements
To all ENFMC organizers and FAPERJ.
Thank you for your attention!
https://sites.google.com/site/mmodashima/
Mariana M. Odashima Introduction to density functional theory XXXVIII ENFMC Foz do Iguac¸u 76/76
ENFMC