The document provides a comprehensive overview of the density-functional tight-binding (DFTB) method, a fast approximate DFT method used in computational materials science. It discusses various DFTB approaches, implementations, and extensions, along with associated resources and literature references. The document highlights the formulation, application, and significance of DFTB and its self-consistent-charge variant in simulating complex material properties.

















![20
Self-consistent-charge density-functional
tight-binding (SCC-DFTB)
M. Elstner et al., Phys. Rev. B 58 7260 (1998)
E r[ ] = ni fi
ˆH r0[ ] fi
i
valence
orbitals
å
1
+ ni fi
ˆH r0[ ] fi
i
core
orbitals
å
2
+ Exc r0[ ]
3
-
1
2
r0VH r0[ ]
R3
ò
4
-
- r0Vxc r0[ ]
R3
ò
5
+ Enucl
6
+
1
2
r1VH r1[ ]
R3
ò
7
+
1
2
d2
Exc
dr1
2
r0
r1
2
R3
òò
8
+ o 2( )
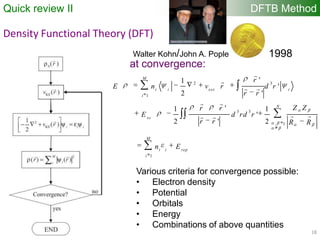
Approximate density functional theory (DFT) method!
Second order-expansion of DFT energy in terms of reference density 0 and
charge fluctuation 1 ( 0 + 1) yields:
Density-functional tight-binding (DFTB) method is derived from terms 1-6
Self-consistent-charge density-functional tight-binding (SCC-DFTB)
method is derived from terms 1-8
o(3)
Lecture II DFTB](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-20-320.jpg)

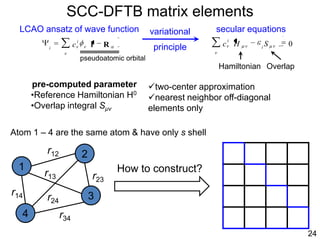
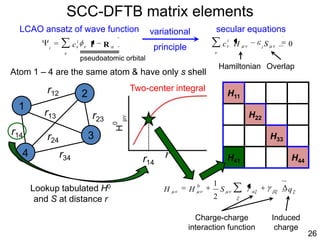
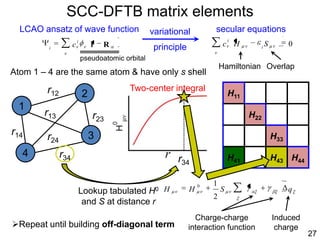
![22
DFTB method
Repulsive diatomic potentials replace usual nuclear repulsion
energy
Reference density 0 is constructed from atomic densities
Kohn-Sham eigenstates i are expanded in Slater basis of valence
pseudoatomic orbitals i
The DFTB energy is obtained by solving a generalized DFTB
eigenvalue problem with H0 computed by atomic and diatomic DFT
r0 = r0
A
A
atoms
å
fi = cmicm
m
AO
å
H0
C = SCe with Smn = cm cn
Hmn
0
= cm
ˆH r0
M
,r0
N
[ ] cn
Lecture II DFTB](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-22-320.jpg)

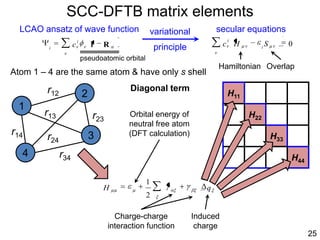






![35
Spin-polarized DFTB (SDFTB)
Lecture II DFTB
for systems with different and spin densities, we have
total density = +
magnetization density S = -
2nd-order expansion of DFT energy at ( 0,0) yields
E r,rS
[ ]= ni fi
ˆH r0[ ] fi
i
valence
orbitals
å
1
+ ni fi
ˆH r0[ ] fi
i
core
orbitals
å
2
+ Exc r0[ ]
3
-
1
2
r0VH r0[ ]
R3
ò
4
-
- r0Vxc r0[ ]
R3
ò
5
+ Enucl
6
+
1
2
r1VH r1[ ]
R3
ò
7
+
1
2
d2
Exc
dr1
2
r0 ,0( )
r1
2
R3
òò
8
+
1
2
d2
Exc
drS
( )
2
r0 ,0( )
rS
( )
2
R3
òò
9
+ o 2( )
The Spin-Polarized SCC-DFTB (SDFTB) method is derived from terms 1-9
o(3)](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-35-320.jpg)




![0 1 2 3 4 5
0
20
40
60
80
40
0 1 2 3 4 5
0
20
40
60
80
0 1 2 3 4 5
0
20
40
60
80
0 1 2 3 4 5
0
20
40
60
80
0 1 2 3 4 5
0
20
40
60
80
Time[ps] Time[ps]Time[ps]
Te= 0K
Te= 1500K
Te= 10kK
Te=0 K always yields SCC convergence problemSCC iterations(time)
Maximum iteration number is 70
0 1 2 3 4 5
0
20
40
60
80
0 1 2 3 4 5
0
20
40
60
80
0 2 4
0
20
40
60
80
0 1 2 3 4 5
0
20
40
60
80
(A) H10C60 Fe38 (B) Fe13C10 (C) Fe6C2
kbTe(10kK) ~0.87 eV
~half-width of 3d band in Fe38
DFTBLecture II](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-40-320.jpg)





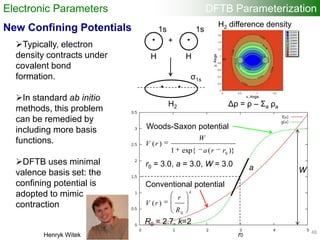
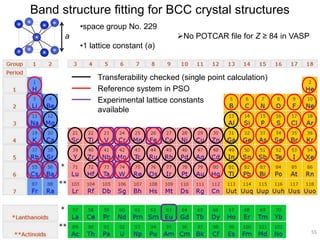
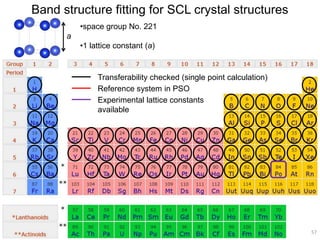
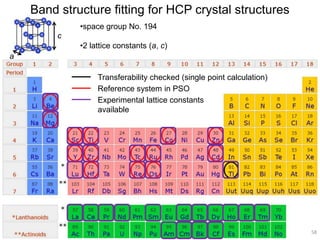
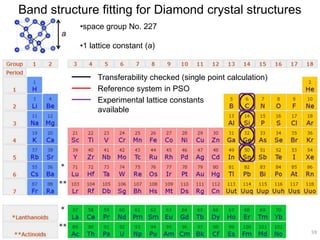
![2). DFTB band structure fitting
•Optimization of parameter sets for Woods-Saxon confining potential (orbital
and density) and unoccupied orbital energies
•Fixed orbital energies for electron occupied orbitals
•Valence orbitals : [1s] for 1st row
[2s, 2p] for 2nd row
[ns, np, md] for 3rd – 6th row
(n ≥ 3, m = n-1 for group 1-12, m = n for group 13-18)
•Fitting points : valence bands + conduction bands (depending on the system,
at least including up to ~+5 eV with respect to Fermi level)
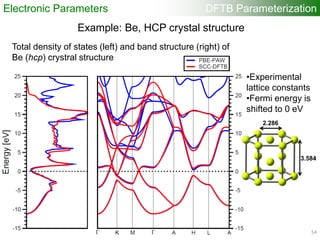
Electronic Parameters DFTB Parameterization
1). DFT band structure calculations
•VASP 4.6
•One atom per unit cell
•PAW (projector augmented wave) method
•32 x 32 x 32 Monkhorst-Pack k-point sampling
•cutoff = 400 eV
•Fermi level is shifted to 0 eV
49](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-49-320.jpg)
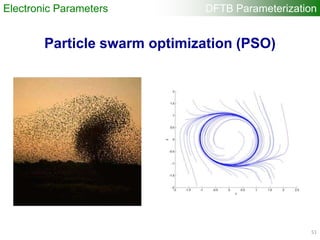
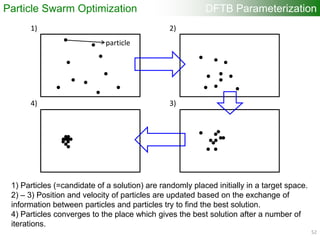
![Each particle has
randomly generated
parameter sets (r0, a, W)
within some region
Generating one-center
quantities (atomic orbitals,
densities, etc.)
“onecent”
Computing two-center
overlap and Hamiltonian
integrals for wide range
of interatomic distances
“twocent”
“DFTB+”
Calculating DFTB band
structure
Update the parameter
sets of each particle
Memorizing the best fitness
value and parameter sets
Evaluating “fitness value”
(Difference DFTB – DFT band
structure using specified fitness
points) “VASP”
DFTB Parameterization
orbital
a [2.5, 3.5]
W [0.1, 0.5]
r0 [3.5, 6.5]
density
a [2.5, 3.5]
W [0.5, 2.0]
r0 [6.0, 10.0]
Particle Swarm Optimization
53](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-53-320.jpg)
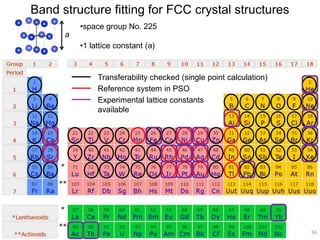
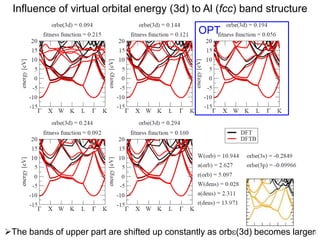
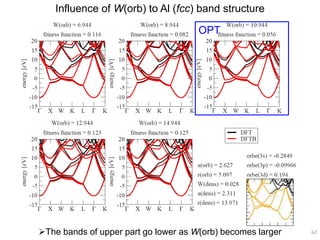
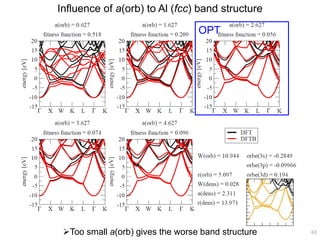
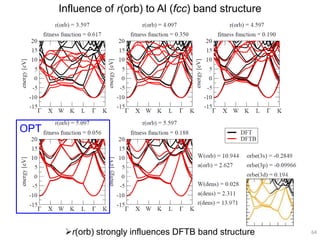
![Correlation of r(orb) vs. atomic diameter
Atomic Number Z
Atomicdiameter[a.u.]
Empirically measured radii
(Slater, J. C., J. Chem. Phys.,
41, 3199-3204, (1964).)
Calculated radii with minimal-
basis set SCF functions
(Clementi, E. et al., J. Chem.
Phys., 47, 1300-1307, (1967).)
Expected value using relativistic
Dirac-Fock calculations
(Desclaux, J. P., Atomic Data
and Nuclear Data Tables, 12,
311-406, (1973).)
This work r(orb)
In particular for main group elements, there seems to be a
correlation between r(orb) and atomic diameter.
65
DFTB ParameterizationElectronic Parameters](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-65-320.jpg)





![74
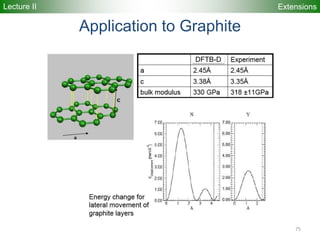
E ~
1/R6
damping f(R ) = [1-exp(-3(rij/Rij,vdW
)7)]3
Rij,vdW = 3.8 Å (for 1st row), 4.8 A (for 2nd row)
DFTB+Dispersion
Elstner et al., JCP 114, 5149 (2001)
DFTB-D choice of C6
parameters:
- generally hybridization
dependent (i.e. not
simply atomic values)
- use “empirical” values
for parameters to match
BSSE-corrected MP2
interaction energies
R [Å]
E [ha]
ExtensionsLecture II](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-74-320.jpg)

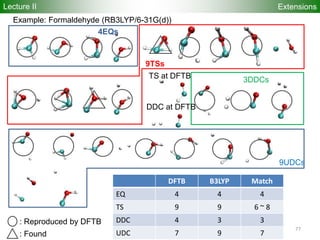


![80
Performance
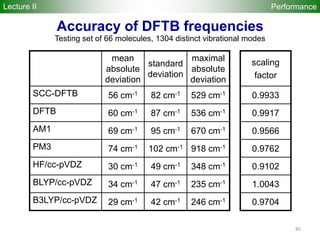
Accuracy of DFTB Geometries and
Energies for Fullerene Isomers
Fullerene Isomers Geometries and Energies vs B3LYP/6-31G(d)
G. Zheng, SI, M.
Elstner, K.
Morokuma, Chem.
Phys. Lett. 412, 210
(2005)
RMS [Å] NCC-DFTB SCC-DFTB AM1 PM3
C20-C36 0.025 0.019 0.035 0.030
C60-C86 0.014 0.014 0.016 0.015
R2
(lin. reg.) NCC-DFTB SCC-DFTB AM1 PM3
C20-C36 0.88 0.93 0.77 0.73
C60-C86 0.97 0.98 0.86 0.84
Geometries
Energetics
•102 Fullerene Isomers
• small cage non-IPR C20-C36 (35), large cage IPR C70-C86 (67)
R2: Energy linear regression between E(Method) and E(B3LYP)
Lecture II](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-80-320.jpg)




![95
A B C
DFT:PW91[1] -6.24 -5.63 -1.82
SCC-DFTB[2] -5.17 -4.68 -1.86
Adhesion energies (eV/atom)
A B C
PW91: An ultrasoft pseudopotential with a plane-wave cutoff of 290 eV for the single metal and the
projector augmented wave method with a plane-wave cutoff of 400 eV for the metal cluster
Fe-Fe and Fe-C DFTB parameters from: G. Zheng et al., J. Chem. Theor. Comput. 3, 1349 (2007)
[1] Phys. Rev. B 75, 115419 (2007) [2] Fermi broadening=0.13 eV
H10C60Fe H10C60Fe
H10C60Fe55
Fe55
icosahedron
H-terminated (5,5) armchair SWNT + Fe atom/cluster
PerformanceLecture II](https://image.slidesharecdn.com/dftb-talk-3427-130702051611-phpapp02/85/Density-Functional-Tight-Binding-DFTB-as-fast-approximate-DFT-method-An-introduction-95-320.jpg)
