This document provides an overview of density functional theory (DFT). It discusses the history and development of DFT, including the Hohenberg-Kohn and Kohn-Sham theorems. The document outlines the fundamentals of DFT, including how it uses functionals of electron density rather than wavefunctions to simplify solving the many-body Schrodinger equation. It also describes the self-consistent approach in DFT calculations and provides examples of popular DFT software packages.

1. .
DENSITY
FUNCTIONAL
THEORY
Project mentor :- Dr. Divya Srivastava
Sandhya Singh
2016MSPH007
M.Sc. Physics,
Department of Physics,
Central University of Rajasthan

2. CONTENTS
• History .
• Background.
• Fundamentals of DFT.
• Working of DFT.
• Example .
• Hohenberg- kohn theorems.
• Energy functional .
• Kohn – sham scheme.
• Doing DFT calculation (practical aspect).

3. HISTORY
1920: INTRODUCTION OF THE THOMAS FERMI MODEL
1964: HOHENBERG-KOHN PAPER PROVING EXISTENCE OF
EXACT DFT
1965: KOHN-SHAM SCHEME INTRODUCED
1970S AND EARLY 80S: DFT BECOMES USEFUL.
1998: NOBEL PRIZE AWARDED TO WALTER KOHN IN
CHEMISTRY FOR DEVELOPMENT OF DFT.

4. BACKGROUND
 To solve many body problems by Schrödinger's equation.
 Only upto one electron problem we can solve
Schrödinger's equation exactly.
 it is very hectic to solve the Schrödinger's equation for a
N- body system.
 We must involve some approximation to solve the problem
a method to obtain an approximate solution to the
Schrödinger's equation of a many body system is DFT.

5. We discuss two parts :
• Part 1 : fundamentals of density functional theory .
o solving many body Schrödinger equation .
o Applications of DFT.
• Part 2: doing DFT calculations - practical aspect .

6. DENSITY FUNCTIONAL THEORY
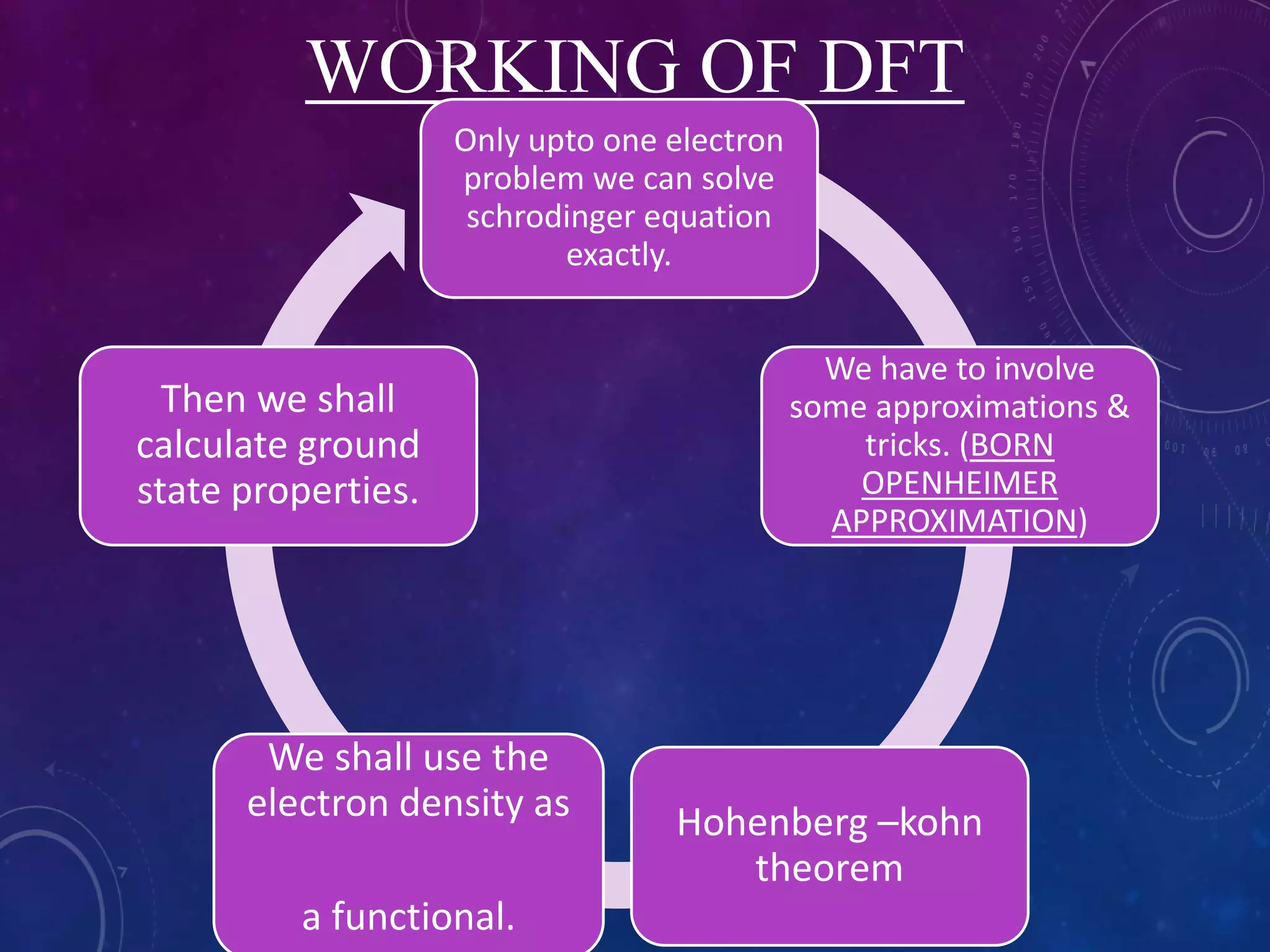
• DFT is a computational quantum mechanical modelling
method used in physics ,chemistry, & material science to
investigate the electronic structure ( ground state) of many
body systems .
• Using this theory the properties of many- electron system
can be determined by using FUNCTIONALS.
• in DFT instead of considering wave function we
considered density functional .
DFT : work in terms of density
E=E[n(r)]
𝜑2=n(r)

7. WORKING OF DFT
Only upto one electron
problem we can solve
schrodinger equation
exactly.
We have to involve
some approximations &
tricks. (BORN
OPENHEIMER
APPROXIMATION)
Hohenberg –kohn
theorem
We shall use the
electron density as
a functional.
Then we shall
calculate ground
state properties.

8. MANY PARTICLE PROBLEMS
• Find the ground state for a collection of atoms by solving
the schrodinger equation
So here we have a bunch of nuclei & bunch of electron which makes the
complicated equation to solve let’s try to atleast a bit simpler .
• If the first thing we do apply B.O. approximation
nuclei they are big (heavy) , slow & electron they are small , fast that
means

9. .
• That means the dynamics of atomic nuclei & electron are separated
so for this calculate ground state energy now
Solve the schrodinger equation for electron :
the electronic Hamiltonian consists of three parts
ℏ

10. .
Density functional theory _ from wavefunction to electron density
it defines the electron density
that reduce to 3N dimensional to 3 spatial dimension. So electron
density is only 3 dimensional.
Now make another approximation HARTREEFOCKAPPROXIMATION
Consider the jth electron is treated as a point charge in the field of all
the other electrons this simplifies the many electron problem to
many one electron problem .so we considered single electron system
we define the electron density in terms of the individual electron wave
function.

11. HOHENBERG – KOHN THEOREMS
Based on two fundamental theorems :
 Theorem 1 : The external potential or the ground state energy
E is a unique functional of electron density .
functional is a function of a function.
 Theorem 2 : The electron density that minimizes the energy
of the overall functional is the true ground state electron density
.
E=E[n(r)]

12. ENERGY FUNCTIONAL
• Two electrons not only interacts via their electronic charge , but
also by their spins & mutual repulsion & attraction .
• Exchange co-relation functional is an approximation that takes
care of all the quantum mechanical information.
• Energy functional consists of two parts one is known & unknown
. Unknown is the exchange co- relation function.

13. KOHN- SHAM SCHEME
• Solve a set of single electron wave function that only depend
on three spatial variable ψ(r) & it is non interacting system.
• The Hamiltonian for single electron system
ℏ

14. SELF – CONSISTENCY SCHEME
Trial n(r)
Solve kohn
equation with
n(r) obtain
single electron
wave function
ψ(r)
Calculate
the electron
density
Calculate
n(r)
Compare
with results

15. .
Step 4 : compare
 If different , then process begins from starting
with new n(r).
 If identical then true ground state density is
obtained .

16. DOING DFT CALCULATION
• There are so many DFT packages (public licence)
• VASP
• QUANTUM EXPRESSO
• ABINIT
• SIESTA
http://cms.mpi.univie.ac.at/vasp/vasp
/vasp.html
www.quantumexpresso.org
www.abinit.org
http://icmab.cat/reem/siesta

17. REFERENCES
The VASP manual
http://cms.mpi.univie.ac.at/vasp/vasp/vasp.html
Electrons.wikidot.com/density -functional –theory
 Book - ABC of DFT
Lecture -by fundamental & application of DFT

18. THANK YOU
• .