Downloaded 177 times
Uploaded byUniversity of California, San Diego
UCSD NANO106 - 01 - Introduction to Crystallography
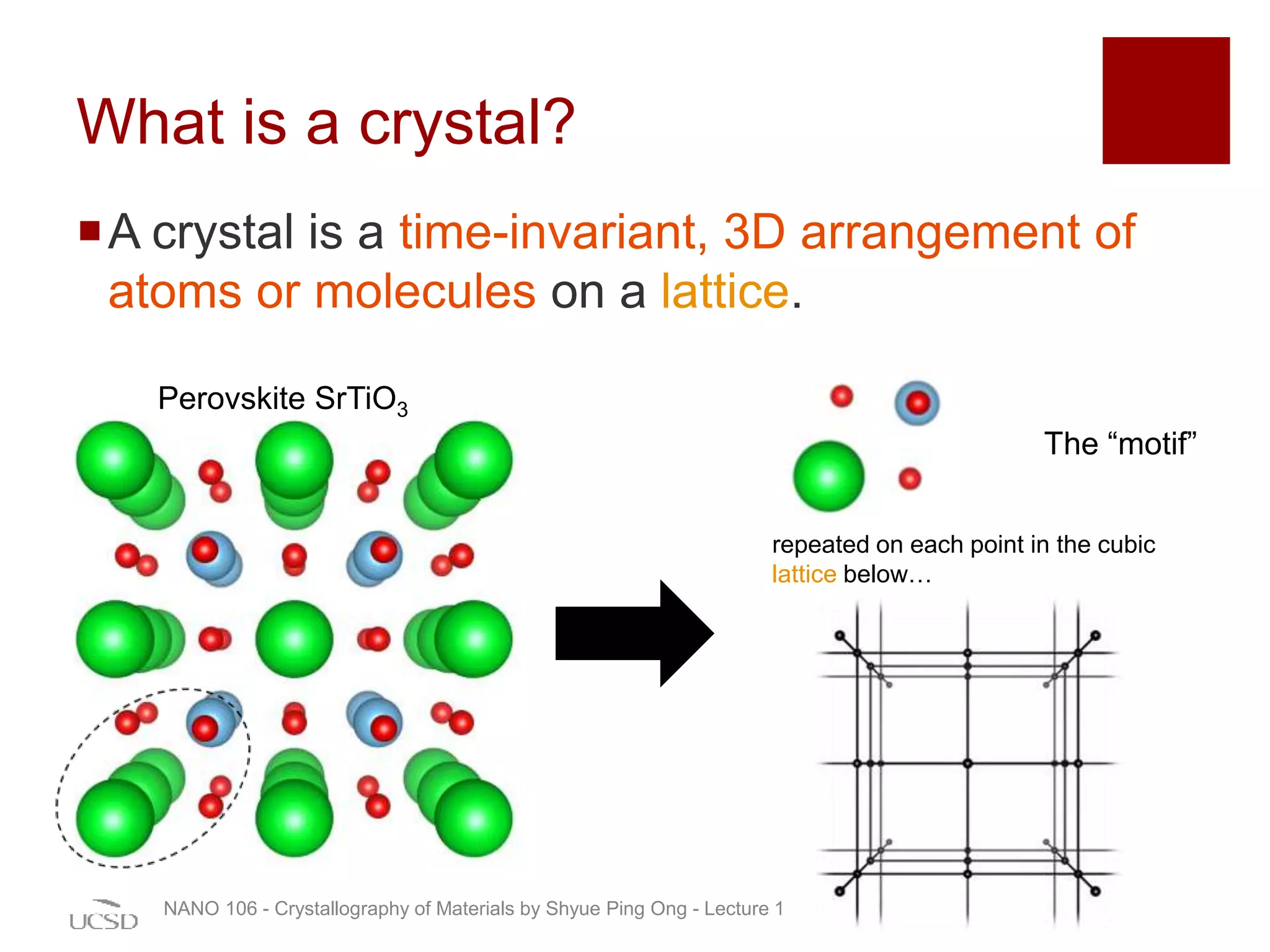
The document discusses the crystallography of materials, focusing on the definition of crystals, lattices, and the concepts of symmetry and translation vectors. It explains the relationships between lattice points, the calculation of lattice parameters, and introduces unit cells, including primitive and non-primitive types. Additionally, it covers higher symmetry nets and the Wigner-Seitz cell as a method for defining regions around lattice points.
More Related Content
Similar to UCSD NANO106 - 01 - Introduction to Crystallography
UCSD NANO106 - 01 - Introduction to Crystallography
- 1. Crystallography of Materials ShyuePing Ong Department of NanoEngineering University of California, San Diego
- 2. Readings ¡Chapter 3 ofStructure of Materials NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1
- 3. What is acrystal? ¡A crystal is a time-invariant, 3D arrangement of atoms or molecules on a lattice. NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 Perovskite SrTiO3 The “motif” repeated on each point in the cubic lattice below…
- 4. Nets and Lattices ¡Alattice (3D) or net (2D) is an abstract concept of an infinite array of discrete points generated by a set of translation operations. NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 The motif Repeated infinitely in all directions
- 5. Concept of Symmetry ¡Youhave just encountered your first symmetry concept – translational symmetry. ¡A symmetry operation is a permutation of atoms such that the molecule or crystal is indistinguishable before and after the operation. ¡It also means that all lattice points have exactly the same “environment”. NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1
- 6. Identify the netsin the following patterns NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1
- 7. Identify the netsin the following patterns NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1
- 8. Basis and translationvectors ¡ How are points in a lattice related to one another (e.g. how do we get from point A to point B)? NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 A B b a Let us define basis vectors a and b. All points in the lattice can therefore be reached by integer linear combinations of the basis vectors, i.e., By inspection, we can see that If we choose A to be the arbitrary origin with coordinates (0, 0), all other lattice points can be represented as (u, v). For example,B = (2, 1). t is then known as the translation vector. t t = ua + vb, u,v ∈ Z B- A = 2a + b
- 9. Basis and translationvectors ¡ For 3D lattices, there are three basis vectors instead of two. Notationally, ¡ And each lattice point/node can be represented by coordinates (u, v, w) NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 t = ua + vb+ wc, u,v,w ∈ Z
- 10. Net and Latticeparameters NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 a = Length of a b = Length of b c = Length of c α = Angle between b and c β = Angle between a and c γ = Angle between a and b a,b,c,α,β,γ{ } a = Length of a b = Length of b γ = Angle between a and b a,b,γ{ }
- 11. Lattice math example ¡Alattice is given by the following vectors in Cartesian space: ¡ Calculate the lattice parameters a, b, c, α, β, γ. ¡ If a lattice node is given by coordinates (3, 2, 1) in crystal coordinates, what are its coordinates in Cartesian coordinates? NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 a = 1 0 0 ! " # # # $ % & & & , b= −1/ 2 3 / 2 0 ! " # # ## $ % & & && , c = 0 0 3 ! " # # # $ % & & & Blackboard
- 12. Deriving the 2DCrystal Systems ¡ What values can take? Or phrased in another way, what special values of would result in additional symmetry? NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 a,b,γ{ } a,b,γ{ } Consider arbitrary a,b,γ{ } What are the symmetry elements in this net? The oblique net (and all 2D nets) has two-fold rotational symmetry.
- 13. Higher symmetry nets NANO106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 a ≠ b,γ = 90° a = b,γ = 90° Rectangular net Square net a = b,γ =120° Hexagonal net
- 14. Adding new nodes ¡Canwe get a new distinct net by adding more lattice points to existing nets? NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 New centered rectangular net, all nodes have the same environment. No new net! If we reorient the lattice by 45 deg, we see that what we have is simply a square net with shorter vectors. Not a net at all. All nodes do not have the same environment.
- 15. Rectangular Five 2D nets NANO106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 p: primitive c: centered (lower case for 2D) International symbols for 2D nets Oblique Square Hexagonal Four 2D crystal systems m: monoclinic o: orthorhombic t: tetragonal h: hexagonal
- 16. Unit Cells NANO 106- Crystallography of Materials by Shyue Ping Ong - Lecture 1 ¡ A unit cell is simply a geometric unit that can be stacked infinitely to reproduce the entire lattice. ¡ Primitive unit cells – only 1 lattice point in the cell ¡ Non-primitive cells – more than 1 lattice point in the cell • Which of these cells are primitive? • How many lattice points are there in each cell? • Which cell(s) reflect the full symmetry of the net?
- 17. The Wigner-Seitz Cell ¡The Wigner-Seitz (WS) cell around a lattice point is defined as the locus of points in space that are closer to that lattice point than to any of the other lattice points. NANO 106 - Crystallography of Materials by Shyue Ping Ong - Lecture 1 The WS cell • is a unit cell, i.e., tiles space to reproduce the lattice; • can have more than 4 sides in 2D and more than 6 sides in 3D; • Preserves symmetry of net/lattice.