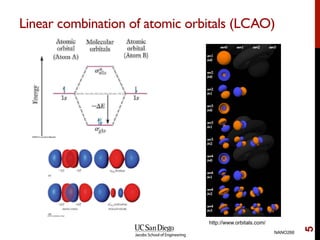
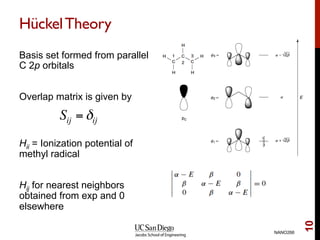
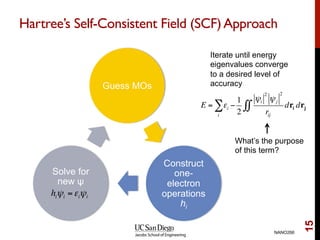
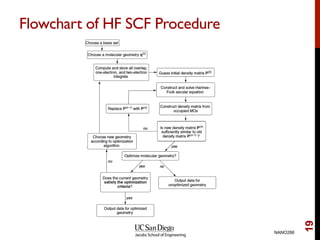
The document discusses the Hartree-Fock approximation and the stationary Schrödinger equation for atomic systems, emphasizing the significance of the variational principle in determining the quality of wave functions based on energy levels. It elaborates on the Linear Combination of Atomic Orbitals (LCAO) approach and the secular equation used to minimize energy in one-electron molecular systems. Additionally, it covers limitations of the Hartree-Fock method, basis sets, and performance considerations, including effective core potentials and strategies to improve computational efficiency.

1. The Hartree-Fock
Approximation
Shyue Ping Ong

2. Stationary Schrödinger Equation for a System of
Atoms
where
NANO266
2
Eψ = Hψ
H = −
h 2
2me
∇i
2
i
∑ −
h 2
2mk
∇k
2
−
e2
Zk
rikk
∑
i
∑ +
e2
rijj
∑
i
∑
k
∑ +
Zk Zle2
rkll
∑
k
∑
KE of electrons
KE of nuclei
Coulumbic attraction
between nuclei and
electrons
Coulombic repulsion
between electrons
Coulombic repulsion
between nuclei

3. Stationary Schrödinger Equation inAtomic Units
To simplify the equations a little, let us from
henceforth work with atomic units
NANO266
3
Dimension Unit Name Unit Symbol
Mass Electron rest mass me
Charge Elementary Charge e
Action Reduced Planck’s constant ħ
Electric constant Coulomb force constant ke
H = −
1
2
∇i
2
i
∑ −
1
2mk
∇k
2
−
Zk
rikk
∑
i
∑ +
1
rijj
∑
i
∑
k
∑ +
Zk Zl
rkll
∑
k
∑

4. TheVariational Principle
We can judge the quality of the wave functions by
the energy – the lower the energy, the better. We
may also use any arbitrary basis set to expand
the guess wave function.
How do we actually use this?
NANO266
4
φHφ dr∫
φ2
dr∫
≥ E0

5. Linear combination of atomic orbitals (LCAO)
NANO266
5
http://www.orbitals.com/

6. Solving the one-electron molecular system with
the LCAO basis set approach
In general, we may express our trial wave functions
as a series of mathematical functions, known as a
basis set.
For a single nucleus, the eigenfunctions are
effectively the hydrogenic atomic orbitals. We may
use these atomic orbitals as a basis set for our
molecular orbitals. This is known as the linear
combination of atomic orbitals (LCAO) approach.
NANO266
6
φ = aiϕi
i=1
N
∑

7. The Secular Equation
NANO266
7
E =
aiϕi
i=1
N
∑
"
#
$
%
&
'H aiϕi
i=1
N
∑
"
#
$
%
&
'dr∫
aiϕi
i=1
N
∑
"
#
$
%
&
'
2
dr∫
=
aiaj ϕiHϕj dr∫
ij
∑
aiaj ϕiϕj dr∫
ij
∑
=
aiaj Hij
ij
∑
aiajSij
ij
∑
Resonance integral
Overlap integral

8. The Secular Equation,contd
To minimize the energy,
Which gives
Or in matrix form
NANO266
8
∂E
∂ak
= 0, ∀k
ai (Hki − ESki )
i=1
N
∑ = 0, ∀k
H11 − ES11 H12 − ES12 ! H1N − ES1N
H21 − ES21 H22 − ES22 ! H2N − ES2N
" " # "
HN1 − ESN1 HN 2 − ESN 2 ! HNN − ESNN
"
#
$
$
$
$
$
%
&
'
'
'
'
'
a1
a2
"
aN
"
#
$
$
$
$
$
%
&
'
'
'
'
'
= 0

9. The Secular Equation,contd
Solutions exist only if
Procedure:
i. Select a set of N basis functions.
ii. Determine all N2 values of Hij and Sij.
iii. Form the secular determinant and determine the N roots Ej.
iv. For each Ej, solve for coefficients ai.
NANO266
9
H11 − ES11 H12 − ES12 ! H1N − ES1N
H21 − ES21 H22 − ES22 ! H2N − ES2N
" " # "
HN1 − ESN1 HN 2 − ESN 2 ! HNN − ESNN
= 0

10. HückelTheory
Basis set formed from parallel
C 2p orbitals
Overlap matrix is given by
Hii = Ionization potential of
methyl radical
Hij for nearest neighbors
obtained from exp and 0
elsewhere
NANO266
10
Sij =δij

11. The Born-OppenheimerApproximation
Heavier nuclei moves much more slowly than
electrons => Electronic relaxation is
“instantaneous” with respect to nuclear motion
Electronic Schrödinger Equation
NANO266
11
(Hel +VN )ψel (qi;qk ) = Eelψel (qi;qk )
Electronic energy
Constant for a set of
nuclear coordinates

12. Stationary Electronic Schrödinger Equation
where
NANO266
12
Eelψel = Helψel
Hel = −
1
2
∇i
2
i
∑ −
Zk
rikk
∑
i
∑ +
1
rijj
∑
i
∑
KE and nuclear attraction terms are separable
H = hi
i
∑ where hi = −
1
2
∇i −
Zk
rikk
∑

13. Hartree-ProductWave Functions
Eigen functions of the one-electron Hamiltonian is given
by
Because the Hamiltonian is separable,
NANO266
13
hiψi =εiψi
ψHP = ψi
i
∏
HψHP = hi
i
∑ ψk
k
∏
= εi
i
∑
#
$
%
&
'
(ψHP

14. The effective potential approach
To include electron-electron repulsion, we use a
mean field approach, i.e., each electron sees an
“effective” potential from the other electrons
NANO266
14
hi = −
1
2
∇i −
Zk
rikk
∑ +Vi, j
where
Vi, j =
ρj
rij
∫
j≠i
∑ dr

15. Hartree’s Self-Consistent Field (SCF)Approach
NANO266
15
Guess MOs
Construct
one-
electron
operations
hi
Solve for
new ψ
hiψi =εiψi
Iterate until energy
eigenvalues converge
to a desired level of
accuracy
E = εi
i
∑ −
1
2
ψi
2
ψj
2
rij
dri drj∫∫
What’s the purpose
of this term?

16. What about the Pauli Exclusion Principle?
Two identical fermions (spin ½ particles) cannot
occupy the same quantum state simultaneously
è Wave function has to be anti-symmetric
For two electron system, we have
NANO266
16
ψSD =
1
2
ψa (1)α(1)ψb (2)α(2)−ψa (2)α(2)ψb (1)α(1)[ ]
=
1
2
ψa (1)α(1) ψb (1)α(1)
ψa (2)α(2) ψb (2)α(2)
where α is the electron spin eigenfunction
Slater determinant

17. For many electrons…
NANO266
17
ψSD =
1
N!
χ1(1) χ2 (1) ! χN (1)
χ1(2) χ2 (2) ! χN (2)
! ! " !
χ1(N) χ2 (N) ! χN (N)
where χk are the spin orbitals

18. The Hartree-Fock (HF) Self-Consistent Field
(SCF) Method
NANO266
18
fi = −
1
2
∇i
2
−
Zk
rik
+Vi
HF
{j}
k
nuclei
∑
F11 − ES11 F12 − ES12 ! F1N − ES1N
F21 − ES21 F22 − ES22 ! F21 − ES2N
" " # "
FN1 − ESN1 FN 2 − ESN 2 ! FNN − ESNN
= 0
HF Secular Equation
Fµυ = µ |−
1
2
∇i
2
|υ − Zk µ |
1
rk
|υ + Pλσ
λσ
∑ (µυ | λσ )−
1
2
(µλ |υσ )
$
%&
'
()
k
nuclei
∑
Weighting of four-index integrals by density
matrix, P

19. Flowchart of HF SCF Procedure
NANO266
19

20. Limitations of HF
Fock operators are one-electron => All electron
correlation, other than exchange, is ignored
Four-index integrals leads to N4 scaling with
respect to basis set size
NANO266
20
Ecorr = Eexact − EHF

21. PracticalAspects of HF Calculations
Basis Sets
Effective
Core
Potentials
Open-shell
vs Closed-
shell
Accuracy
Performance
NANO266
21

22. Basis Set
Set of mathematical functions used to construct
the wave function.
In theory, HF limit is achieved by an infinite basis
set.
In practice, use finite basis sets that can
approach HF limit as efficiently as possible
NANO266
22

23. Contracted Gaussian Functions
Slater-type orbitals (STO) with
radial decay cannot be
analytically integrated
-> Use linear combination of
Gaussian-type orbitals (GTOs)
with radial decay to
approximate STOs
STO-3G
• STO approximated by 3 GTOs
• Known as single-ζ or minimal basis set.
NANO266
23
e−r2
e−r

24. Multiple-ζ and Split-Valence
Multiple-ζ
• Adding more basis functions per atomic orbital
• Examples: cc-pCVDZ, cc-pCVTZ (correlation-consistent polarized
Core and Valence (Double/Triple/etc.) Zeta)
Split-valence or Valence-Multiple-ζ
• Still represent core orbitals with single, contracted basis functions
• Valence orbitals are split into many functions (Why?)
• Examples: 3-21G, 6-31G, 6-311G
NANO266
24
# of primitives in
core
# of primitives in
valence

25. Polarization and Diffuse Functions
Polarization functions
• Description of MOs require more flexibility than provided by AOs,
e.g., NH3 is predicted to be planar if using just s and p functions
• Additional basis functions of one quantum number of higher
angular momentum than valence, e.g., first row -> d orbitals
• Notation: 6-31G* [old] or 6-31G(d) [new], 6-31(2d,p) [2d functions
for heavy atoms, additional p for H]
Diffuse functions
• Highest energy MOs of anions, highly excited states tend to be
more diffuse
• Augment standard basis sets with diffuse functions
• Notation: 6-31+G, 6-311++G(3df, 2pd), aug-cc-pCVDZ
NANO266
25

26. Effective Core Potentials
Heavy atoms have many electrons
• Intractable to model all of them, even with a minimal basis set
• However, most of the electrons are in the core
Solution: Replace core electrons with analytical
functions (effective core potentials or ECPs) that
represent combined nuclear-electronic core to the
remaining electrons
Key selection decision: How many electrons to
include in the core?
NANO266
26

27. Open-shell vs closed-shell
Restricted HF (RHF)
• Closed-shell systems, i.e., no unpaired electrons
Restricted open-shell HF (ROHF)
• Use RHF formalism, but with density matrix for singly occupied
orbitals not multiplied by a factor of 2.
• Wave functions are eigenfunctions of S2
• But fails to account for spin polarization in doubly occupied orbitals
Unrestricted HF (UHF)
• Includes spin polarization
• Wave functions are not eigenfunctions of S2, i.e., spin contamination
NANO266
27

28. Accuracy
Energetics
• In general, extremely poor; correlation is extremely important in
chemical bonding!
• Protonation energies are typically ok (no electrons in H+)
• Koopman’s Theorem: First IE is equal to the negative of the
orbital energy of the HOMO
Geometry
• Typically relatively good ground state structures with basis sets of
modest size
• But transition states (with partial bonding) can be problematic, as
well as some pathological systems
NANO266
28

29. Performance
Formal N4 scaling
But in reality, speedups can be achieved through:
• Symmetry
• Estimating upper bounds to four-index integrals
• Fast multipole and linear exchange integral computations
For practical geometry optimizations, frequently
helps to first compute geometry with a smaller
basis set to provide a better initial geometry and a
guess for the Hessian matrix.
NANO266
29