Download as PDF, PPTX
Uploaded byUniversity of California, San Diego
NANO266 - Lecture 3 - Beyond the Hartree-Fock Approximation
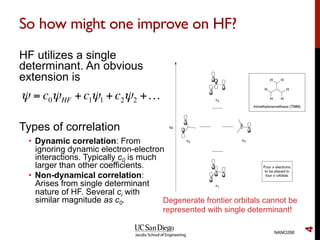
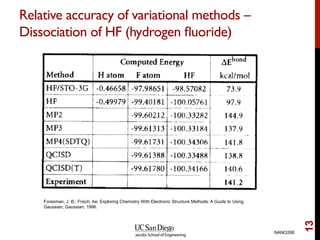
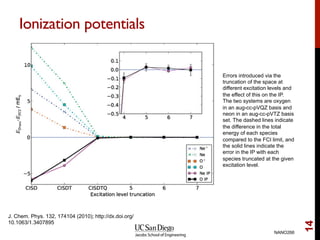
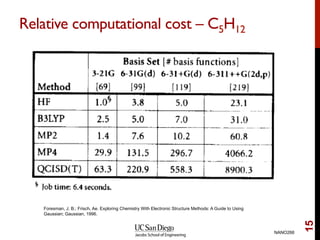
The document discusses the limitations of the Hartree-Fock (HF) approximation in quantum chemistry, particularly regarding the treatment of electron correlation. It explores various advanced methods, such as Møller-Plesset perturbation theory and coupled-cluster methods, for improving upon HF, emphasizing the importance of understanding both dynamic and non-dynamical correlation. Additionally, it highlights the computational costs associated with these methods and provides references for further detailed study.
More Related Content
Similar to NANO266 - Lecture 3 - Beyond the Hartree-Fock Approximation
More from University of California, San Diego
NANO266 - Lecture 3 - Beyond the Hartree-Fock Approximation
- 1.
- 2. Overview In this lecture,we will only touch on conceptual underpinnings of how correlation is included, without going too much into the details of the methods. Most of the advanced methods are far too computationally expensive and limited to small system sizes, which makes them less useful for the materials scientist at this time. It suffices that you understand them at a conceptual level, and if you are interested (or they become more accessible in future), there are many excellent works on the subject. NANO266 2
- 3. Limitations of HF Allcorrelation, other than exchange, is ignored in HF NANO266 3 Ecorr = Eexact − EHF
- 4. So how mightone improve on HF? HF utilizes a single determinant. An obvious extension is Types of correlation • Dynamic correlation: From ignoring dynamic electron-electron interactions. Typically c0 is much larger than other coefficients. • Non-dynamical correlation: Arises from single determinant nature of HF. Several ci with similar magnitude as c0. NANO266 4 ψ = c0ψHF +c1ψ1 +c2ψ2 +… Degenerate frontier orbitals cannot be represented with single determinant!
- 5. Multiconfiguration SCF Optimize orbitalsfor a combination of configurations (orbital occupations) • Configuration state function (CSF): molecular spin state and occupation number of orbitals • Active space: orbitals that are allowed to be partially occupied (based on chemistry of interest) Scaling CAS: Complete active space (CASSCF) NANO266 5 # of singlet CSFs for m electrons in n orbitals = n!(n +1)! m 2 ! " # $ % &! m 2 +1 ! " # $ % &! n − m 2 ! " # $ % &! n − m 2 +1 ! " # $ % &!
- 6. Full Configuration Interaction(CI) CASSCF calculation of all orbitals and all electrons Best possible calculation within limits of basis set For small systems, can be used to benchmark other methods NANO266 6 Full CI Infinite Basis Set Exact solution to Schodinger Equation
- 7. Limiting excitations inCI CIS (CI singles) • Used for excited states • No use for ground states CID (CI doubles) CISD (CI singles doubles) • N6 scaling NANO266 7
- 8. Møller–Plesset perturbation theory Treatsexact Hamiltonian as a perturbation on sum of one- electron Fock operators NANO266 8 H = H(0) + λV = fi i ∑ + λV Expanding the ground-state eigenfunctions and eigenvalues as Taylor series in λ, ψ =ψ(0) + λψ(1) + λ2 ψ(2) +… a = a(0) + λa(1) + λ2 a(2) +… where ψ(k) = 1 k! ∂k ψ ∂λk and a(k) = 1 k! ∂k a ∂λk H ψ = a ψ ∴(H(0) + λV) λk ψ(k) ∑ = λk a(k) λk ψ(k) ∑∑ By equating powers of λ and imposing normalization, we can derive a(k) , which are the kth order corrections to a(0) .
- 9. MPnTheory MP1 is simplyHF MP2 • Second-order energy correction • Analytic gradients available • N5 scaling MPn > 2 • No analytic gradients available • > 95% of electron correlation at n=4. NANO266 9
- 10. Issues in PerturbationApproach Perturbationtheory works best when perturbation is small (convergence of Taylor series expansion) • In MPn, perturbation is full electron-electron repulsion! MPn is not variational! (possible for correlation to be larger than exact, but in practice, basis set limitations cause errors in opposite direction) NANO266 10
- 11. Coupled-Cluster Full-CI wave functioncan be described as If we truncate at T2 CCSD(T) • Includes single/triples coupling term • Analytic gradients and second derivatives available • Gold-standard in most quantum chemistry calculations NANO266 11 ψ = eT ψHF where T = T1 + T2 + T3 +…+ Tn is the cluster operator ψCCSD = (1+(T1 + T2 )+ (T1 + T2 )2 2! +…)ψHF
- 12. Practical Considerations Basis setconvergence is a bigger problem for correlated calculations Performance vs Accuracy • HF < MP2 ~ MP3 < CCD < CISD < QCISD ~CCSD < MP4 < QCISD(T) ~ CCSD(T) NANO266 12 Highly expensive, but accurate!
- 13. Relative accuracy ofvariational methods – Dissociation of HF (hydrogen fluoride) NANO266 13 Foresman, J. B.; Frisch, Ae. Exploring Chemistry With Electronic Structure Methods: A Guide to Using Gaussian; Gaussian, 1996.
- 14. Ionization potentials NANO266 14 Errors introducedvia the truncation of the space at different excitation levels and the effect of this on the IP. The two systems are oxygen in an aug-cc-pVQZ basis and neon in an aug-cc-pVTZ basis set. The dashed lines indicate the difference in the total energy of each species compared to the FCI limit, and the solid lines indicate the error in the IP with each species truncated at the given excitation level. J. Chem. Phys. 132, 174104 (2010); http://dx.doi.org/ 10.1063/1.3407895
- 15. Relative computational cost– C5H12 NANO266 15 Foresman, J. B.; Frisch, Ae. Exploring Chemistry With Electronic Structure Methods: A Guide to Using Gaussian; Gaussian, 1996.
- 16. Bond lengths NANO266 16 Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; 2004.
- 17. Parameterized methods G2/G3 theoryfor accurate thermochemistry (errors < 4 kcal / mol) NANO266 17
- 18. References Essentials of ComputationalChemistry: Theories and Models by Christopher J. Cramer NANO266 18