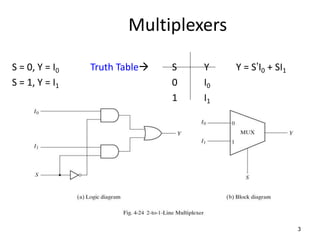
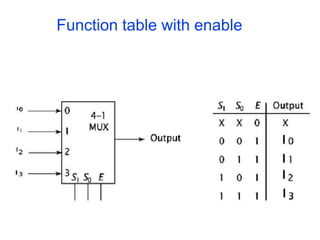
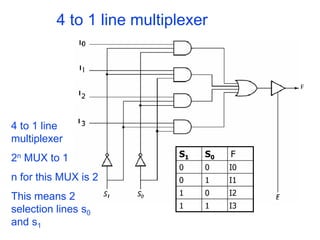
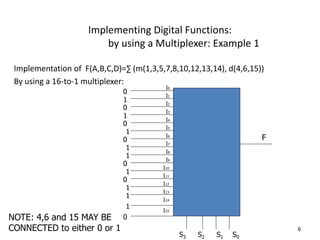
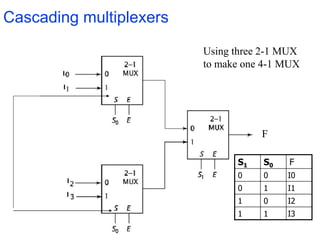
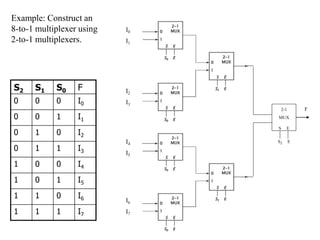
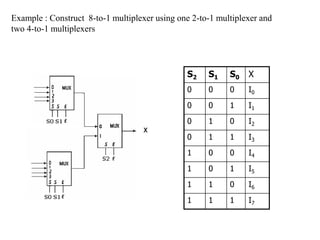
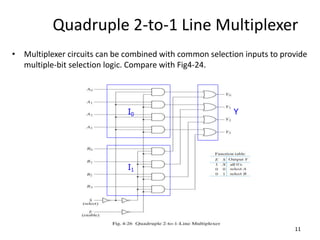
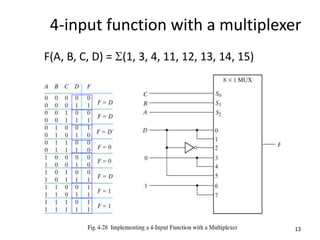
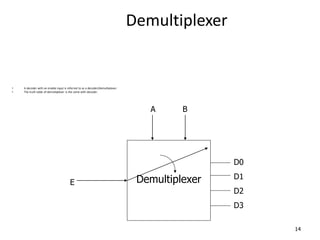
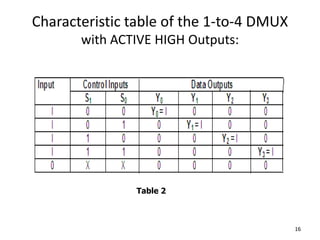
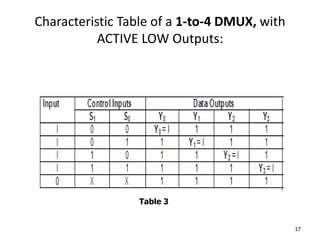
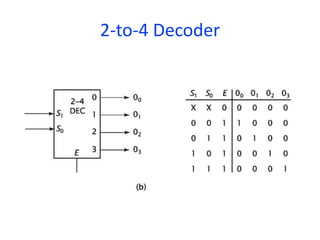
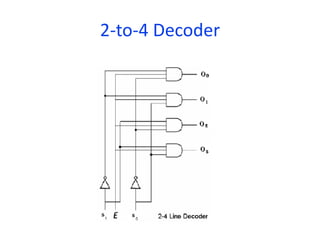
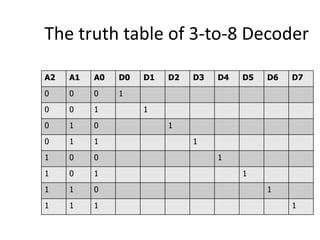
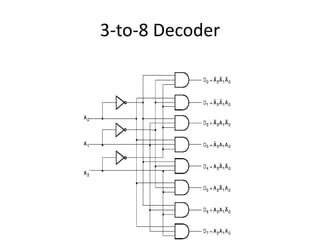
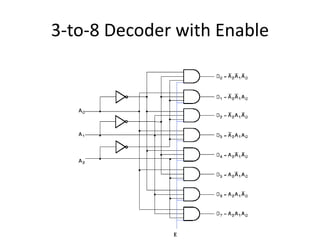
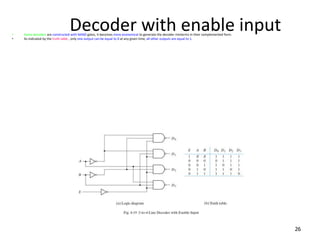
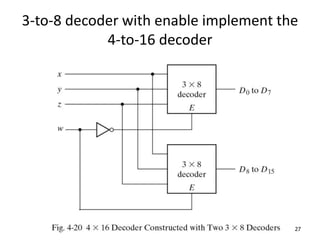
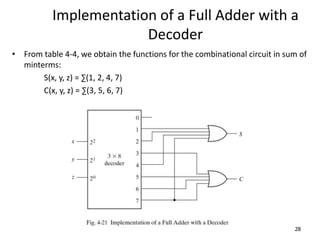
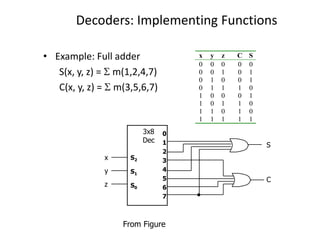
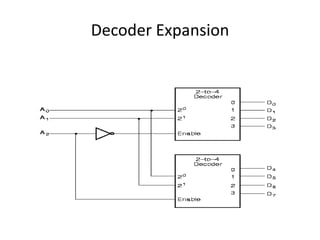
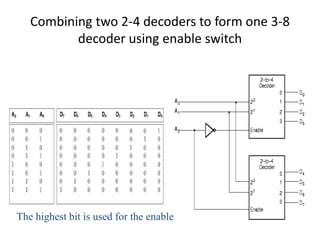
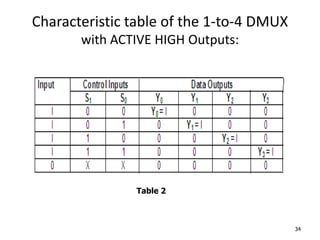
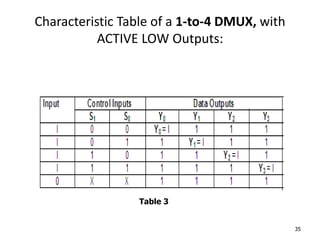
A multiplexer is a combinational logic circuit that selects one of several input lines and outputs the data on that line. It has 2n input lines and n selection lines, where the values on the selection lines determine which input line is output. For example, a 2-to-1 multiplexer has two inputs and one selection line, outputting either the first or second input depending on the selection line value. Multiplexers can be cascaded to build larger multiplexers. Boolean functions can also be implemented using multiplexers. A demultiplexer is similar but has one input and multiple outputs, using the selection lines to determine which output is activated. Decoders are similar to demultiplexers but are used to

1. Combinational Logic Design
Unit II

2. Multiplexer
• It is a combinational circuit that selects binary
information from one of the input lines and directs it
to a single output line
• Usually there are 2n input lines and n selection lines
whose bit combinations determine which input line
is selected
• For example for 2-to-1 multiplexer if selection S is
zero then I0 has the path to output and if S is one I1
has the path to output (see the next slide)

3. Multiplexers
S = 0, Y = I0 Truth Table S Y Y = S’I0 + SI1
S = 1, Y = I1 0 I0
1 I1
3

4. Function table with enable

5. 4 to 1 line multiplexer
S1 S0 F
0 0 I0
0 1 I1
1 0 I2
1 1 I3
4 to 1 line
multiplexer
2n MUX to 1
n for this MUX is 2
This means 2
selection lines s0
and s1

6. Implementing Digital Functions:
by using a Multiplexer: Example 1
Implementation of F(A,B,C,D)=∑ (m(1,3,5,7,8,10,12,13,14), d(4,6,15))
By using a 16-to-1 multiplexer:
6
F
I0
0
0
1
0
NOTE: 4,6 and 15 MAY BE
CONNECTED to either 0 or 1
I1
I2
I3
I4
I5
I8
I6
I9
I7
I11
I10
I13
I12
I14
I15
0
0
0
0
1
1
1
1
1
1
1
1
S3 S2 S1 S0

7. Boolean function Implementation
• Another method for implementing boolean
function is using multiplexer
• For doing that assume boolean function has n
variables. We have to use multiplexer with n-1
selection lines and
• 1- first n-1 variables of function is used for data
input
• 2- the remaining single variable is used for data
input. Each data input can be z, z’, 1 or 0. From
truth table we have to find the relation of F and
z to be able to design input lines. For example :
f(x,y,z) = ∑(1,2,6,7)

8. Cascading multiplexers
Using three 2-1 MUX
to make one 4-1 MUX
S1 S0 F
0 0 I0
0 1 I1
1 0 I2
1 1 I3
F

9. F
2-1
MUX
S E
S2 E
S2 S1 S0 F
0 0 0 I0
0 0 1 I1
0 1 0 I2
0 1 1 I3
1 0 0 I4
1 0 1 I5
1 1 0 I6
1 1 1 I7
I0
I1
I2
I3
I4
I5
I6
I7
Example: Construct an
8-to-1 multiplexer using
2-to-1 multiplexers.

10. Example : Construct 8-to-1 multiplexer using one 2-to-1 multiplexer and
two 4-to-1 multiplexers
S2 S1 S0 X
0 0 0 I0
0 0 1 I1
0 1 0 I2
0 1 1 I3
1 0 0 I4
1 0 1 I5
1 1 0 I6
1 1 1 I7

11. Quadruple 2-to-1 Line Multiplexer
• Multiplexer circuits can be combined with common selection inputs to provide
multiple-bit selection logic. Compare with Fig4-24.
11
I0
I1
Y

12. Boolean function implementation
• A more efficient method for implementing a Boolean function of
n variables with a multiplexer that has n-1 selection inputs.
F(x, y, z) = (1,2,6,7)
12

13. 4-input function with a multiplexer
F(A, B, C, D) = (1, 3, 4, 11, 12, 13, 14, 15)
13

14. Demultiplexer
• A decoder with an enable input is referred to as a decoder/demultiplexer.
• The truth table of demultiplexer is the same with decoder.
14
Demultiplexer
D0
D1
D2
D3
E
A B

15. Demultiplexer (DMUX)/ Decoder
A 1-to-m DMUX, with ACTIVE HIGH Outputs, has
• 1 Input: I ( also called as the Enable input when the
device is called a Decoder)
• m ACTIVE HIGH Outputs: Y0, Y1, Y2,
..................................... …………….Y(m-1)
• n Control inputs: S0, S1, S2, ...... S(m-1)
15

16. Characteristic table of the 1-to-4 DMUX
with ACTIVE HIGH Outputs:
16
Table 2

17. Characteristic Table of a 1-to-4 DMUX, with
ACTIVE LOW Outputs:
17
Table 3

18. Decoder
– Accepts a value and decodes it
• Output corresponds to value of n inputs
– Consists of:
• Inputs (n)
• Outputs (2n , numbered from 0  2n - 1)
• Selectors / Enable (active high or active low)

19. A Decoder is a Demultiplexer with a change in
the name of the inputs :
19
Y0
Y1
Y2
Y4
S1 S0
ENABLE
INPUT
2 to 4
Decoder
When the IC is used as a Decoder, the input I is called
an Enable input

20. The truth table of 2-to-4 Decoder

21. 2-to-4 Decoder

22. 2-to-4 Decoder

23. The truth table of 3-to-8 Decoder
A2 A1 A0 D0 D1 D2 D3 D4 D5 D6 D7
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1

24. 3-to-8 Decoder

25. 3-to-8 Decoder with Enable

26. Decoder with enable input
• Some decoders are constructed with NAND gates, it becomes more economical to generate the decoder minterms in their complemented form.
• As indicated by the truth table , only one output can be equal to 0 at any given time, all other outputs are equal to 1.
26

27. 3-to-8 decoder with enable implement the
4-to-16 decoder
27

28. Implementation of a Full Adder with a
Decoder
• From table 4-4, we obtain the functions for the combinational circuit in sum of
minterms:
S(x, y, z) = ∑(1, 2, 4, 7)
C(x, y, z) = ∑(3, 5, 6, 7)
28

29. Decoders: Implementing Functions
• Example: Full adder
S(x, y, z) =  m(1,2,4,7)
C(x, y, z) =  m(3,5,6,7)
3x8
Dec
S2
S1
S0
x
y
z
0
1
2
3
4
5
6
7
S
C
x y z C S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
From Figure

30. Decoder Expansion
• Decoder expansion
– Combine two or more small decoders with enable
inputs to form a larger decoder
– 3-to-8-line decoder constructed from two 2-to-4-
line decoders
• The MSB is connected to the enable inputs
• if A2=0, upper is enabled; if A2=1, lower is
enabled.

31. Decoder Expansion

32. Combining two 2-4 decoders to form one 3-8
decoder using enable switch
The highest bit is used for the enables

33. How about 4-16 decoder
• Use how many 3-8 decoder?
• Use how many 2-4 decoder?

34. Characteristic table of the 1-to-4 DMUX
with ACTIVE HIGH Outputs:
34
Table 2

35. Characteristic Table of a 1-to-4 DMUX, with
ACTIVE LOW Outputs:
35
Table 3