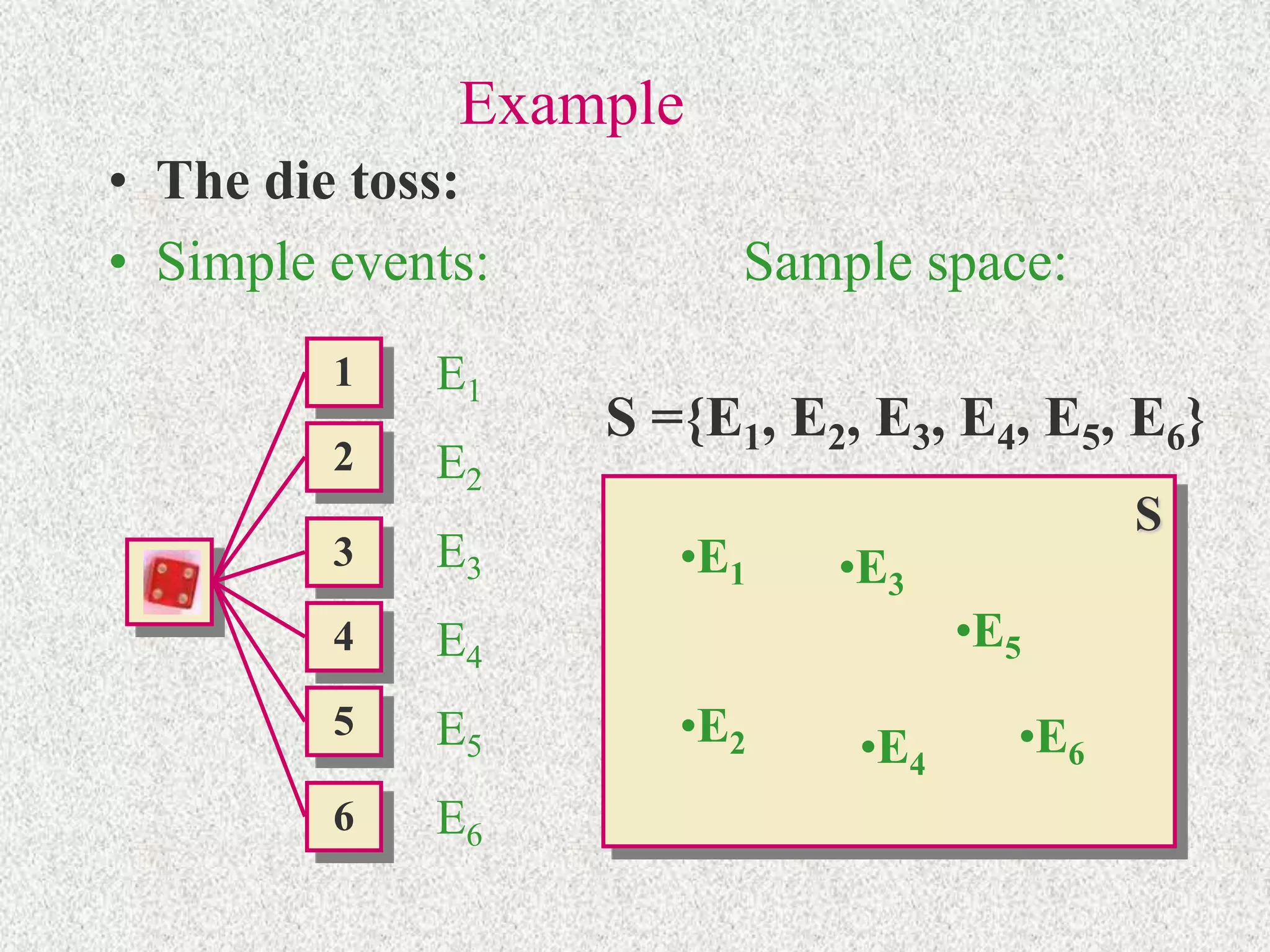
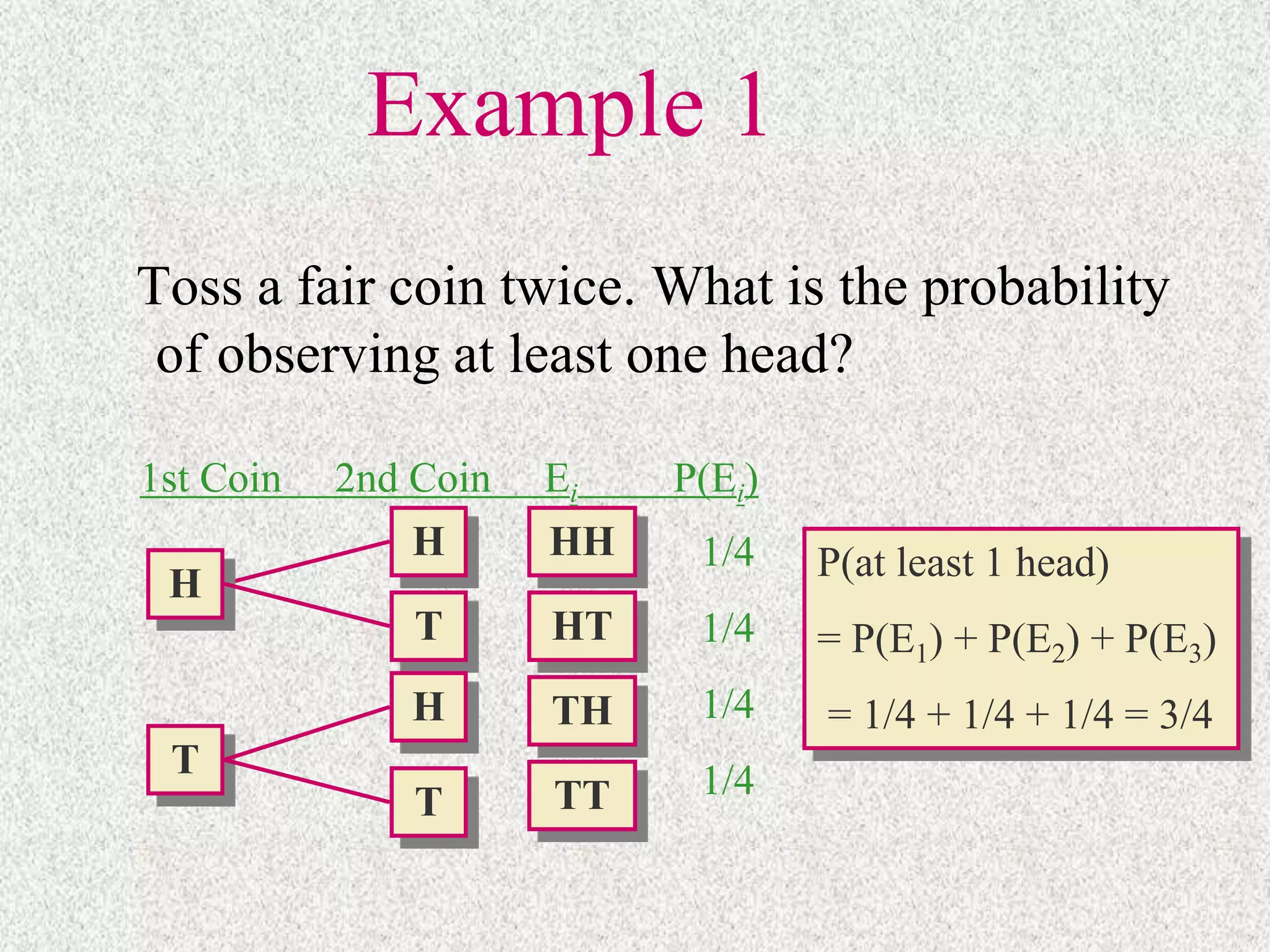
This document provides an overview of probability concepts including: - Probability is a numerical measure of the likelihood of an event occurring, ranging from 0 (impossible) to 1 (certain). - An experiment generates outcomes that make up the sample space. Events are collections of outcomes. - Simple events have a defined probability based on being equally likely. The probability of an event is the sum of probabilities of the simple events it contains. 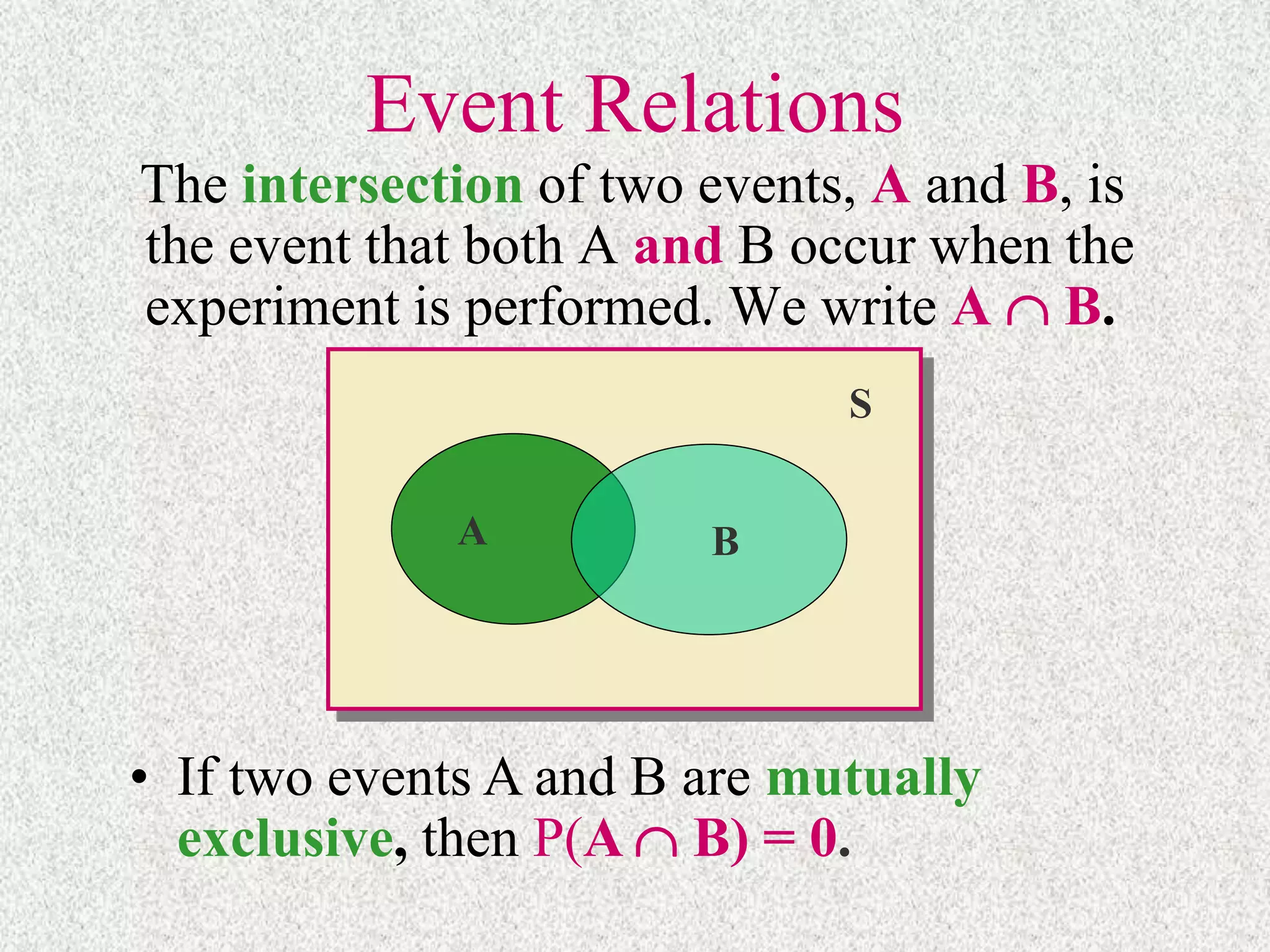- Rules like the multiplication rule for independent events and additive rule for unions allow calculating probabilities of composite events. - Complement and conditional probabilities relate the probabilities of events. Independent events do not influence each other's probabilities.

1. PROBABILITY
BY UNSA SHAKIR

2. What is a PROBABILITY?
- Probability is the chance that some event will happen
- It is the ratio of the number of ways a certain event
can occur to the number of possible outcomes
Probability of Simple Events

3. Probability as a Numerical Measure
of the Likelihood of Occurrence
0 1.5
Increasing Likelihood of Occurrence
Probability
The event
is very
unlikely
to occur.
The occurrence
of the event is
just as likely as
it is unlikely.
The event
is almost
certain
to occur.

4. An Experiment and Its Sample Space
An experiment is any process that generates
well-defined outcomes.
The sample space for an experiment is the set of
all experimental outcomes.
An experimental outcome is also called a sample
point.

5. An event is a collection of sample points.
The probability of any event is equal to the sum of
the probabilities of the sample points in the event.
If we can identify all the sample points of an
experiment and assign a probability to each, we
can compute the probability of an event.
Events and Their Probabilities

6. An Experiment and Its Sample Space
Experiment
Toss a coin
Inspection a part
Conduct a sales call
Roll a die
Play a football game
Experiment Outcomes
Head, tail
Defective, non-defective
Purchase, no purchase
1, 2, 3, 4, 5, 6
Win, lose, tie

7. Using Simple Events
• The probability of an event A is equal to
the sum of the probabilities of the simple
events contained in A
• If the simple events in an experiment are
equally likely, you can calculate
eventssimpleofnumbertotal
Aineventssimpleofnumber
)( 
N
n
AP A

8. The Probability of an Event
• P(A) must be between 0 and 1.
– If event A can never occur, P(A) = 0. If
event A always occurs when the experiment
is performed, P(A) =1.
• The sum of the probabilities for all simple
events in S equals 1.

9. Example
• The die toss:
• Simple events: Sample space:
1
2
3
4
5
6
E1
E2
E3
E4
E5
E6
S ={E1, E2, E3, E4, E5, E6}
S
•E1
•E6
•E2
•E3
•E4
•E5

10. Basic Concepts
• An event is a collection of one or more simple
events.
•The die toss:
–A: an odd number
–B: a number > 2
S
A ={E1, E3, E5}
B ={E3, E4, E5, E6}
B
A
•E1
•E6
•E2
•E3
•E4
•E5

11. – Suppose that 10% of the U.S. population has
red hair. Then for a person selected at random,
Finding Probabilities
• Probabilities can be found using
–Estimates from empirical studies
–Common sense estimates based on
equally likely events.
P(Head) = 1/2
P(Red hair) = .10
• Examples:
–Toss a fair coin.

12. Example 1
Toss a fair coin twice. What is the probability
of observing at least one head?
H
1st Coin 2nd Coin Ei P(Ei)
H
T
T
H
T
HH
HT
TH
TT
1/4
1/4
1/4
1/4
P(at least 1 head)
= P(E1) + P(E2) + P(E3)
= 1/4 + 1/4 + 1/4 = 3/4

13. Example 2
A bowl contains three M&Ms®, one red, one
blue and one green. A child selects two M&Ms
at random. What is the probability that at least
one is red?
1st M&M 2nd M&M Ei P(Ei)
RB
RG
BR
BG
1/6
1/6
1/6
1/6
1/6
1/6
P(at least 1 red)
= P(RB) + P(BR)+ P(RG)
+ P(GR)
= 4/6 = 2/3
m
m
m
m
m
m
m
m
m
GB
GR

14. Example 3
The sample space of throwing a pair of dice is

15. Example 3
Event Simple events Probability
Dice add to 3 (1,2),(2,1) 2/36
Dice add to 6 (1,5),(2,4),(3,3),
(4,2),(5,1)
5/36
Red die show 1 (1,1),(1,2),(1,3),
(1,4),(1,5),(1,6)
6/36
Green die show 1 (1,1),(2,1),(3,1),
(4,1),(5,1),(6,1)
6/36

16. • I have 40 candies
• 26 are Red
• 4 are Blue
• 10 are Yellow
• I’m going to take out one.
Example:

17. • Q: What is the probability of getting a red candy?
• A: 13/20 or 0.65
• Q: What is the probability of getting a yellow
candy?
• A: ¼ or 0.25
• Q:What is the probability of getting a blue candy
• A: 1/10 or o.1
Question andAnswers

18. Example
• A random sample of size two is to be selected from the list
of six cities, San Diego, Los Angeles, San Francisco,
Denver, Paris, and London.
• A company has offices in six cities, San Diego, Los
Angeles, San Francisco, Denver, Paris, and London. A new
employee will be randomly assigned to work in one of these
offices.
Outcomes ?
Sample Space ?

19. Real World Example:
Best Buy is having an IPOD giveaway. They put all the
IPOD Shuffles in a bag. Customers may choose an
IPOD without looking at the color. Inside the bag are
4 orange, 5 blue, 6 green, and 5 pink IPODS. If
Maria chooses one IPOD at random, what is the
probability she will choose an orange IPOD?
P(orange) = 4/20 = 2/10 = 1/5 or 20%
Probability of Simple Events

20. Example : Deck of Cards.
What is the probability of picking a heart?
# favorable outcomes 13 1
# possible outcomes 52 4
The probability of picking a heart is
1 out of 4 or .25 or 25%
What is the probability of picking a non heart?
# favorable outcomes 39 3
# possible outcomes 52 4
The probability of picking a heart is
3 out of 4 or .75 or 75%
Probability of Simple Events
P(heart) = = =
P(nonheart) = =

21. Real World Example:
A computer company manufactures 2,500
computers each day. An average of 100 of
these computers are returned with defects.
What is the probability that the computer
you purchased is not defective?
P(not defective) = # not defective = 2,400 = 24
total # manufactured 2,500 25
Probability of Simple Events

22. Probability Examples
●A jar contains 30 red marbles, 12 yellow
marbles, 8 green marbles and 5 blue marbles. What
is the probability that you draw and replace marbles
3 times and you get NO red marbles?
• There are 55 marbles, 25 of which are not red
• P(getting a color other than red) = P(25/55) ≈ .455
• Probability of this happening 3 times in a row is
found by .455*.455*.455 ≈ .094

23. Multiplication Rule and
Independent Events
Multiplication Rule for Independent Events: Let A and B
be two independent events, then
( ) ( ) ( ).P A B P A P B 
Examples:
• Flip a coin twice. What is the probability of observing two
heads?
• Flip a coin twice. What is the probability of getting a head
and then a tail? A tail and then a head? One head?
Three computers are ordered. If the probability of getting a
“working” computer is .7, what is the probability that all three
are “working” ? .7 x .7 x .7=.7³ =.343 or 34.3%……

24. S
Event Relations
The beauty of using events, rather than simple events, is that we
can combine events to make other events using logical operations:
and, or and not.
The union of two events, A and B, is the event that either A or B
or both occur when the experiment is performed. We write
A B
A B

25. S
A B
Event Relations
The intersection of two events, A and B, is
the event that both A and B occur when the
experiment is performed. We write A B.
• If two events A and B are mutually
exclusive, then P(A B) = 0.

26. S
Event Relations
A
AC
sometimes, we want to know the probability that an event
will not happen; an event opposite to the event of interest is
called a complementary event.
If A is an event, its complement is The probability of the
complement is AC or A
Example: The complement of male event is the female

27. Example
Select a student from the classroom and
record his/her hair color and gender.
– A: student has brown hair
– B: student is female
– C: student is male
What is the relationship between events B and C?
•AC:
•BC:
•BC:
Mutually exclusive; B = CC
Student does not have brown hair
Student is both male and female = 
Student is either male and female = all students = S

28. Calculating Probabilities for Unions and
Complements
• There are special rules that will allow you to
calculate probabilities for composite events.
• The Additive Rule for Unions:
• For any two events, A and B, the probability
of their union, P(A B), is
)()()()( BAPBPAPBAP 
A B

29. Example: Additive Rule
Example: Suppose that there were 120 students
in the classroom, and that they could be
classified as follows: total Brown Not Brown
Male 60 20 40
Female 60 30 30
A: brown hair
P(A) = 50/120
B: female
P(B) = 60/120
P(AB) = P(A) + P(B) – P(AB)
= 50/120 + 60/120 - 30/120
= 80/120 = 2/3 Check: P(AB)
= (20 + 30 + 30)/120

30. Example: Two Dice
A: red die show 1
B: green die show 1
P(AB) = P(A) + P(B) – P(AB)
= 6/36 + 6/36 – 1/36
= 11/36

31. A Special Case
When two events A and B are
mutually exclusive, P(AB) = 0
and P(AB) = P(A) + P(B).
Brown Not Brown
Male 20 40
Female 30 30
A: male with brown hair
P(A) = 20/120
B: female with brown hair
P(B) = 30/120
P(AB) = P(A) + P(B)
= 20/120 + 30/120
= 50/120
A and B are mutually
exclusive, so that

32. Example: Two Dice
A: dice add to 3
B: dice add to 6
A and B are mutually
exclusive, so that
P(AB) = P(A) + P(B)
= 2/36 + 5/36
= 7/36

33. Calculating Probabilities
for Complements
• We know that for any event A:
–P(A AC) = 0
• Since either A or AC must occur,
P(A AC) =1
• so that P(A AC) = P(A)+ P(AC) = 1
P(AC) = 1 – P(A)
A
AC

34. Example
Brown Not Brown
Male 20 40
Female 30 30
A: male
P(A) = 60/120
B: female
P(B) = ?
P(B) = 1- P(A)
= 1- 60/120 = 60/120
A and B are
complementary, so that
Select a student at random from
the classroom. Define:

35. Example
• A jar contains 30 red marbles, 12 yellow marbles, 8
green marbles and 5 blue marbles.What is the probability
that you draw and replace marbles 3 times and you get at
least 1 Red?
• It's easier to calculate the probability of getting NO red
marbles, and subtract that from 1 (we use the complement
rule : P(AC) = 1 – P(C)
• From previous example, it is 1 - .094 = .906

36. Calculating Probabilities for
Intersections
In the previous example, we found P(A  B) directly
from the table. Sometimes this is impractical or
impossible. The rule for calculating P(A  B) depends
on the idea of independent and dependent events.
Two events, A and B, are said to be independent if the
occurrence or nonoccurrence of one of the events does
not change the probability of the occurrence of the
other event.

37. Conditional Probabilities
The probability that A occurs, given that event
B has occurred is called the conditional
probability of A given B and is defined as
0)(if
)(
)(
)|( 

 BP
BP
BAP
BAP
“given”

38. Example 1
Toss a fair coin twice. Define
– A: head on second toss
– B: head on first toss
HT
TH
TT
1/4
1/4
1/4
1/4
P(A|B) = ½
P(A|not B) = ½HH
P(A) does not
change, whether
B happens or
not…
A and B are
independent!

39. Example 2
A bowl contains five M&Ms®, two red and three
blue. Randomly select two candies, and define
– A: second candy is red.
– B: first candy is blue.
P(A|B) =P(2nd red|1st blue)= 2/4 = 1/2
P(A|not B) = P(2nd red|1st red) = 1/4
P(A) does change,
depending on
whether B happens
or not…
A and B are
dependent!

40. Example 3: Two Dice
Toss a pair of fair dice. Define
– A: red die show 1
– B: green die show 1
P(A|B) = P(A and B)/P(B)
=1/36/1/6=1/6=P(A)
P(A) does not
change, whether
B happens or
not…
A and B are
independent!

41. Example 3: Two Dice
Toss a pair of fair dice. Define
– A: add to 3
– B: add to 6
P(A|B) = P(A and B)/P(B)
=0/36/5/6=0
P(A) does change
when B happens
A and B are dependent!
In fact, when B happens,
A can’t

42. Problem .
Blood
Group
Males Females Total
O
A
B
AB
20
17
8
5
20
18
7
5
40
35
15
10
Total 50 50 100

43. Problem .
Ill Not Ill Total
Ate Barbecue
Did Not Eat Barbecue
90
20
30
60
120
80
Total 110 90 200
An outbreak of food poisoning occurs in a group
of students who attended a party

44. Conditional probabilities
Example: If a subject was selected randomly and
found to be female what is the probability that she
has a blood group O
Here the total possible outcomes constitute a
subset (females) of the total number of subjects.
This probability is termed probability of O given F
P(OF) = 20/50
= 0.40

45. Example:
probability of being male &
belong to blood group AB
P(M and AB) = P(M∩AB)
= 5/100
= 0.05
∩ = intersection

46. Example
The joint probability of being male and having blood
type O
To know that two events are independent compute
the marginal and conditional probabilities of one of
them if they are equal the two events are
independent. If not equal the two events are
dependent
P(O) = 40/100 = 0.40
P(OM) = 20/50 = 0.40
Then the two events are independent
P(O∩M) = P(O)P(M) = (40/100)(50/100)
= 0.20

47. Example:
The joint probability of being ill and eat barbecue
P(Ill) = 110/200 = 0.55
P(IllEat B) = 90/120 = 0.75
Then the two events are dependent
P(Ill∩Eat B) = P(Eat B)P(IllEat B)
= (10/200)(90/120)
= 0.45

48. Example:
The probability of being either blood type O or
blood type A
P(OUA) = P(O) + P(A)
= (40/100)+(35/100)
= 0.75

49. Two events are not mutually exclusive
(male gender and blood type O).
P(M OR O) = P(M)+P(O) – P(M∩O)
= 0.50 + 0.40 – 0.20
= 0.70
Example:

50. Excercises
1. If tuberculous meningitis had a case fatality of 20%,
(a) Find the probability that this disease would be fatal in
two randomly selected patients (the two events are
independent)
(b) If two patients are selected randomly what is the
probability that at least one of them will die?
(a) P(first die and second die) = 20%  20% = 0.04
(b) P(first die or second die)
= P(first die) + P(second die) - P(both die)
= 20% + 20% - 4%
= 36%

51. 2. In a normally distributed population, the probability that a
subject’s blood cholesterol level will be lower than 1 SD
below the mean is 16% and the probability of being blood
cholesterol level higher than 2 SD above the mean is
2.5%. What is the probability that a randomly selected
subject will have a blood cholesterol level lower than 1 SD
below the mean or higher than 2 SD above the mean.
P(blood cholesterol level < 1 SD below the mean or 2 SD
above the mean) = 16% + 2.5%
= 18.5%

52. 3. In a study of the optimum dose of lignocaine required to reduce
pain on injection of an intravenous agent used for induction of
anesthesia, four dosing groups were considered (group A
received no lignocaine, while groups B, C, and D received 0.1,
0.2, and 0.4 mg/kg, respectively). The following table shows the
patients cross-classified by dose and pain score:
Pain
score
Group Total
A B C D
0
1
2
3
49
16
8
4
73
7
5
1
58
7
6
0
62
8
6
0
242
38
25
5
Total 77 86 71 76 310
Compute the following probabilities for a
randomly selected patient:
1.being of group D and experiencing
no pain
2.belonging to group B or having a
pain score of 2
3.having a pain score of 3 given that
he belongs to group A
4.belonging to group C

53. Nightlights and Myopia
Assuming these data are representative of a larger population,
what is the approximate probability that someone from that
population who sleeps with a nightlight in early childhood
will develop some degree of myopia?
Note: 72 + 7 = 79 of the 232 nightlight users developed some
degree of myopia. So the probability to be 79/232 = 0.34.

54. Defining Independence
• We can redefine independence in terms of
conditional probabilities:
Two events A and B are independent if and only if
P(A|B) = P(A) or P(B|A) = P(B)
Otherwise, they are dependent.
• Once you’ve decided whether or not two events
are independent, you can use the following rule
to calculate their intersection.

55. The Multiplicative Rule for Intersections
• For any two events, A and B, the probability that
both A and B occur is
P(A B) = P(A) P(B given that A occurred)
= P(A)P(B|A)
• If the events A and B are independent, then the
probability that both A and B occur is
P(A B) = P(A) P(B)

56. Example 1
In a certain population, 10% of the people can be
classified as being high risk for a heart attack. Three
people are randomly selected from this population.
What is the probability that exactly one of the three are
high risk?
Define H: high risk N: not high risk
P(exactly one high risk) = P(HNN) + P(NHN) + P(NNH)
= P(H)P(N)P(N) + P(N)P(H)P(N) + P(N)P(N)P(H)
= (.1)(.9)(.9) + (.9)(.1)(.9) + (.9)(.9)(.1)= 3(.1)(.9)2 = .243

57. Example 2
Suppose we have additional information in the
previous example. We know that only 49% of the
population are female. Also, of the female patients, 8%
are high risk. A single person is selected at random. What
is the probability that it is a high risk female?
Define H: high risk F: female
From the example, P(F) = .49 and P(H|F) = .08.
Use the Multiplicative Rule:
P(high risk female) = P(HF)
= P(F)P(H|F) =.49(.08) = .0392

58. Counting Rules
• Sample space of throwing 3 dice has 216 entries,
sample space of throwing 4 dice has 1296 entries,
…
• At some point, we have to stop listing and start
thinking …
• We need some counting rules

59. The mn Rule
• If an experiment is performed in two stages,
with m ways to accomplish the first stage and
n ways to accomplish the second stage, then
there are mn ways to accomplish the
experiment.
• This rule is easily extended to k stages, with
the number of ways equal to
n1 n2 n3 … nk
Example: Toss two coins. The total number of
simple events is:
2  2 = 4

60. Examples
Example: Toss three coins. The total number of
simple events is: 2  2  2 = 8
Example: Two M&Ms are drawn from a dish
containing two red and two blue candies. The total
number of simple events is:
6  6 = 36
Example: Toss two dice. The total number of simple
events is:
4  3 = 12
Example: Toss three dice. The total number of
simple events is: 6  6  6 = 216

61. Permutation:
Example: A lock consists of five parts and
can be assembled in any order. A quality
control engineer wants to test each order for
efficiency of assembly. How many orders are
there?
120)1)(2)(3)(4(5
!0
!55
5 P
The order of the choice is
important!

62. Example of Combinations
• A box contains six M&Ms®, four red
and two green. A child selects two M&Ms at
random. What is the probability that exactly
one is red?
The order of
the choice is
not important! Ms.&M2choosetoways
15
)1(2
)5(6
!4!2
!66
2 C
M.&Mgreen1
choosetoways
2
!1!1
!22
1 C
M.&Mred1
choosetoways
4
!3!1
!44
1 C 4  2 =8 ways to
choose 1 red and 1
green M&M.
P(exactly one
red) = 8/15

63. Example
A deck of cards consists of 52 cards, 13 "kinds"
each of four suits (spades, hearts, diamonds, and
clubs). The 13 kinds are Ace (A), 2, 3, 4, 5, 6, 7,
8, 9, 10, Jack (J), Queen (Q), King (K). In many
poker games, each player is dealt five cards from
a well shuffled deck.
handspossible
960,598,2
1)2)(3)(4(5
48)49)(50)(51(52
)!552(!5
!52
areThere 52
5 

C

64. Example
Four of a kind: 4 of the 5 cards are the same
“kind”. What is the probability of getting four of
a kind in a five card hand?
and
There are 13 possible choices for the kind of
which to have four, and 52-4=48 choices for
the fifth card. Once the kind has been
specified, the four are completely determined:
you need all four cards of that kind. Thus there
are 13×48=624 ways to get four of a kind.
The probability=624/2598960=.000240096

65. Example
One pair: two of the cards are of one kind, the
other three are of three different kinds.
What is the probability of getting one pair in a
five card hand?
kindthatofcardsfourtheof
twoofchoicespossible6arethere
choice,given thepair;ahavewhich toof
kindfor thechoicespossible13areThere
4
2 C

66. Example
There are 12 kinds remaining from which to select
the other three cards in the hand. We must insist
that the kinds be different from each other and
from the kind of which we have a pair, or we
could end up with a second pair, three or four of a
kind, or a full house.

67. Example
422569.
989601098240/25yprobabilitThe
1,098,240.64220613
ishandspair"one"ofnumbertheTherefore
three.allofsuitsfor thechoices644of
totalacards,threethoseofeachofsuitfor the
choices4areTherecards.threeremainingthe
ofkindspick thetoways220areThere
3
12
3




C

68. Key Concepts
I. Experiments and the Sample Space
1. Experiments, events, mutually exclusive events,
simple events
2. The sample space
II. Probabilities
1. Relative frequency definition of probability
2. Properties of probabilities
a. Each probability lies between 0 and 1.
b. Sum of all simple-event probabilities equals 1.
3. P(A), the sum of the probabilities for all simple events in A

69. Key Concepts
III. Counting Rules
1. mn Rule; extended mn Rule
2. Permutations:
3. Combinations:
IV. Event Relations
1. Unions and intersections
2. Events
a. Disjoint or mutually exclusive: P(A B)  0
b. Complementary: P(A)  1  P(AC )
)!(!
!
)!(
!
rnr
n
C
rn
n
P
n
r
n
r





70. Key Concepts
3. Conditional probability:
4. Independent and dependent events
5. Additive Rule of Probability:
6. Multiplicative Rule of Probability:
)(
)(
)|(
BP
BAP
BAP


)()()()( BAPBPAPBAP 
)|()()( ABPAPBAP 