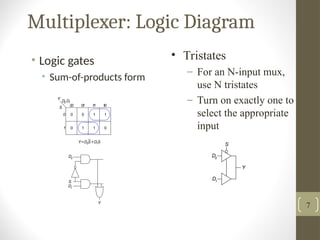
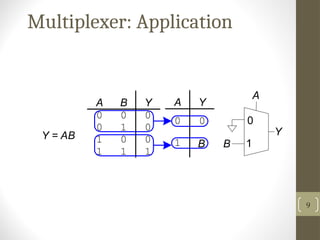
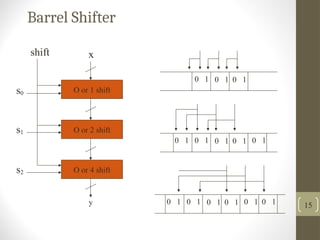
The document discusses various combinational circuits, particularly focusing on multiplexers, which select between multiple inputs based on control signals. It describes the definition, logic diagrams, applications, and examples of implementing boolean functions using multiplexers. Additionally, it touches upon demultiplexers and barrel shifters as related concepts.

1. Combinational Circuits
1

2. 2
Part III. Standard Modules
Interconnect Modules:
1. Decoder, 2. Encoder
3. Multiplexer, 4. Demultiplexer

3. Multiplexer
• Definition
• Logic Diagram
• Application
3

4. 3. Mux (Multiplexer): Definition
4
Description
If En = 1
y = Di where i = (Sn-1, .. , S0)
Else
y = 0
En
y
D2
n
-1-D0
(Data input)
Sn-1,0
(Control input)

5. Multiplexer (Mux): Definition
• Selects between one of N inputs to
connect to the output.
• log2N-bit select input – control input
• Example: 2:1 Mux
Y
0 0
0 1
1 0
1 1
0
1
0
1
0
0
0
0
0 0
0 1
1 0
1 1
1
1
1
1
0
0
1
1
0
1
S
D0
Y
D1
D1 D0
S Y
0
1 D1
D0
S
5

6. 6
Multiplexer Definition: Example
En
y
S1 S0
D0
D1
D2
D3
0
1
2
3
If D0 = 0 and S1S0 = 00 => y = 0
If D0 = 1 and S1S0 = 00 => y = 1

7. Multiplexer: Logic Diagram
• Logic gates
• Sum-of-products form
Y
D0
S
D1
D1
Y
D0
S
S
00 01
0
1
Y
1
1 10
D0 D1
0
0
0
1
1
1
1
0
Y=D0S +D1S
7
• Tristates
– For an N-input mux,
use N tristates
– Turn on exactly one to
select the appropriate
input

8. Multiplexer Application
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
Y = AB
00
Y
01
10
11
A B
8
• Mux for a Boolean function with
truth table as input

9. Multiplexer: Application
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
Y = AB
A Y
0
1
0 0
1
A
B
Y
B
9

10. Multiplexer Application: universal set {Mux}
10
Example 1: Given f (a,b,c) = m (0,1,7) + d(2), implement
with an 8-input Mux.
Id a b c f
0 0 0 0 1
1 0 0 1 1
2 0 1 0 -
3 0 1 1 0
4 1 0 0 0
5 1 0 1 0
6 1 1 0 0
7 1 1 1 1
En
y
1
1
0
0
0
0
0
1
a b c
S2 S1 S0
0
1
2
3
4
5
6
7

11. a
0
0
1
1
b
0
1
0
1
c = 0
1
-
0
0
c = 1
1
0
0
1
D (c)
D0 (c) =1
D1 (c) =0
D2 (c) =0
D3 (c) =c
En
y
1
0
c
a b
S1 S0
0
0
1
2
3
Multiplexer Application
Example 2: Given f (a,b,c) = m (0,1,7) + d(2), implement
with 4-input Muxes.
11

12. a
0
1
00 01 10 11
1 1 - 0
0 0 0 1
D (b,c)
D0 (b,c)
D1 (b,c)
D1 (b,c)
b
0
1
c = 0
0
0
c = 1
0
1
l1(0) = 0
l1(c) = c
En
En b’ 0
1
a
b
y
0
1
0
c
D0 (b,c) = b’ D1 (b,c) = bc
1 -
1 0
c
b
0 0
0 1
c
b
Multiplexer Application
Example 3: Given f (a,b,c) = m (0,1,7) + d(2), implement
with 2-input Muxes.
12

13. 4. Demultiplexers
13
En
x y2n-1 -y0
S(n-1,0)
Control Input
yi = x if i = (Sn-1, .. , S0) & En = 1
yi = 0 otherwise

14. Shifter
14
Can be implemented with a mux
s
d
yi
En
1
0
3 2 1 0
xi+1 xi-1
xi
s
d
xn x0 x-1
xn-1
yn-1 y0
En
s / n
l / r
yi = xi-1 if En = 1, s = 1, and d = L
= xi+1 if En = 1, s = 1, and d = R
= xi if En = 1, s = 0
= 0 if En = 0

15. Barrel Shifter
15
O or 1 shift
O or 2 shift
O or 4 shift
x
s0
s1
s2
y
0 1 0 1 0 1
0 1 0 1 0 1
0 1 0 1
0 1 0 1 0 1
0 1 0 1 0 1
shift