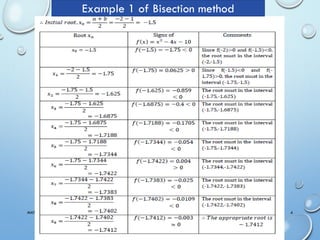
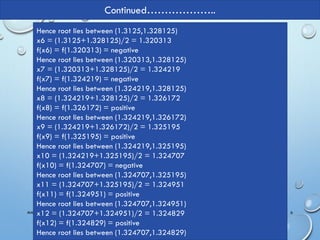
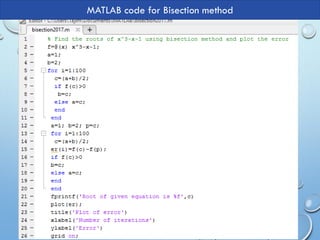
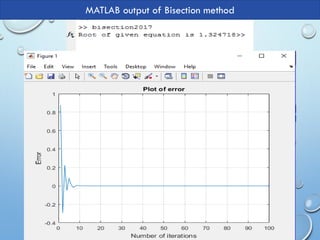
The document covers the bisection method for finding roots of a function using MATLAB, detailing the procedure for determining root approximations between two points, (a,b). It includes an example where the root of the equation x^3 - x = 1 is found by iteratively halving the interval based on the sign of the function at midpoint values. Lastly, an algorithm and MATLAB code snippet for implementing the bisection method are provided.

1. IT-2210 : Computational
mathematics LAB with
MATLAB
4/10/2017MATLAB by Tajim 1

2. Lecture 5: MATLAB – Bisection method.
4/10/2017MATLAB by Tajim 2

3. 4/10/2017MATLAB by Tajim 3
Bisection method
Let us assume that we have to find out the roots of f(x), whose solution is
lies in the range (a,b), which we have to determine. The only condition for
bisection method is that f(a) and f(b) should have opposite signs (f(a)
negative and f(b) positive). When f(a) and f(b) are of opposite signs at
least one real root between ‘a’ and ‘b’ should exist.
For the first approximation we assume that root to be,
x0=(a+b)/2
Then we have to find sign of f(x0).
If f(x0) is negative the root lies between a and x0. If f(x0) is positive the
root lies between x0 and b. Now we have new minimized range, in which
our root lies.
The next approximation is given by, x1 = (a+x0)/2………….if f(x0) is negative. x1 =
(x0+b)/2………….if f(x0) is positive. In this taking midpoint of range of approximate
roots, finally both values of range converges to a single value, which we can take as a
approximate root.

4. 4/10/2017MATLAB by Tajim 4
Example 1 of Bisection method

5. 4/10/2017MATLAB by Tajim 5
Example 2: Find the root of x^3 – x = 1 by using Bisection Method.
Let us assume that the root of x^3 – x – 1=0 lies
between (1,2)
Here, f(1) = negative and f(2) = positive.
Hence root lies between (1,2)
For first approximation,
x0 = (1+2)/2 = 1.5
f(x0) = f(1.5) = positive
Hence root lies between (1,1.5)
x1 = (1+1.5)/2 = 1.25
f(x1) = f(1.25) = negative
Hence root lies between (1.25,1.5)
x2 = (1.25+1.5)/2 = 1.375
f(x2) = f(1.375) = positive
Hence root lies between (1.25,1.375)
x3 = (1.25+1.375)/2 = 1.3125
f(x3) = f(1.3125) = negative
Hence root lies between (1.3125,1.375)
x4 = (1.3125+1.375)/2 = 1.34375
f(x4) = f(1.34375) = positive
Hence root lies between (1.3125,1.34375)
x5 = (1.3125+1.34375)/2 = 1.328125
f(x5) = f(1.328125) = positive

6. 4/10/2017MATLAB by Tajim 6
Continued………………..
Hence root lies between (1.3125,1.328125)
x6 = (1.3125+1.328125)/2 = 1.320313
f(x6) = f(1.320313) = negative
Hence root lies between (1.320313,1.328125)
x7 = (1.320313+1.328125)/2 = 1.324219
f(x7) = f(1.324219) = negative
Hence root lies between (1.324219,1.328125)
x8 = (1.324219+1.328125)/2 = 1.326172
f(x8) = f(1.326172) = positive
Hence root lies between (1.324219,1.326172)
x9 = (1.324219+1.326172)/2 = 1.325195
f(x9) = f(1.325195) = positive
Hence root lies between (1.324219,1.325195)
x10 = (1.324219+1.325195)/2 = 1.324707
f(x10) = f(1.324707) = negative
Hence root lies between (1.324707,1.325195)
x11 = (1.324707+1.325195)/2 = 1.324951
f(x11) = f(1.324951) = positive
Hence root lies between (1.324707,1.324951)
x12 = (1.324707+1.324951)/2 = 1.324829
f(x12) = f(1.324829) = positive
Hence root lies between (1.324707,1.324829)

7. 4/10/2017MATLAB by Tajim 7
Continued………………..
x13 = (1.324707+1.324829)/2 = 1.324768
f(x13) = f(1.324768) = positive
Hence root lies between (1.324707,1.324768)
OK stop it …. I know you are getting tired… but
there is no shortcut.
Now if you observe two limits (1.324707,
1.324768) of above range, they are almost same.
Which is our root of given equation.
Answer: x=1.3247

8. 4/10/2017MATLAB by Tajim 8
Algorithm for Bisection method
1. Input function and limits.
2. Repeat steps 3 and 4 100 times.
3. x=(a+b)/2
4. If f(x0)<0, a=x else b=x
5. Display x
6. Repeat steps 7 and 8 10 times.
7. Error = x-(a+b)/2
8. Store error values in array
9. Plot error
10. STOP.

9. 4/10/2017MATLAB by Tajim 9
MATLAB code for Bisection method

10. 4/10/2017MATLAB by Tajim 10
MATLAB output of Bisection method

11. 4/10/2017MATLAB by Tajim 11
End of
LECTURE five
Thank You .
References: MSK and MMS sir’s
lecture.