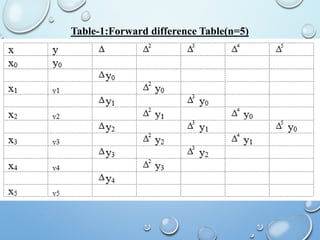
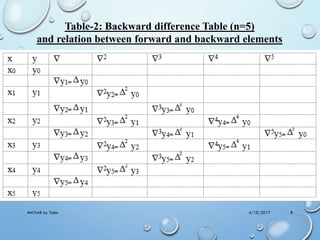
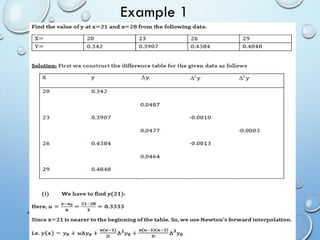
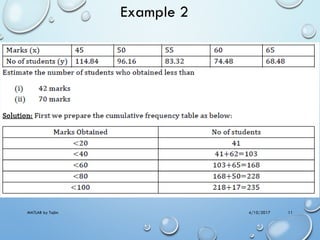
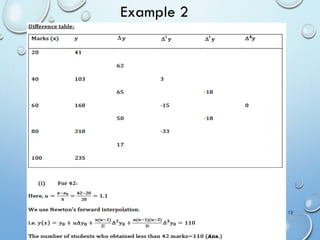
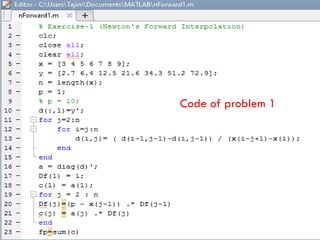
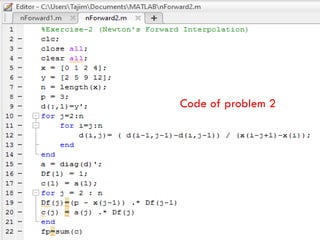
The document outlines a MATLAB lab experiment focused on Newton's forward and backward interpolation methods. It details the objectives of the experiment, which include programming to determine values of y and x from a given set of tabular data using various interpolation formulas. Additionally, the document presents theory, examples of the methods, and MATLAB code outputs related to the problems discussed.

1. IT-2210 : Computational
mathematics LAB with
MATLAB
4/10/2017MATLAB by Tajim 1

2. Lecture 7: MATLAB – Newton's
Forward and back-word
Interpolation
method.
4/10/2017MATLAB by Tajim 2

3. 4/10/2017MATLAB by Tajim 3
Interpolation

4. 4/10/2017MATLAB by Tajim 4
Linear Interpolation

5. 4/10/2017MATLAB by Tajim 5
Objective of the Experiment:
•To get introduce with different interpolating formulae.
•To write a program in order to find out the value of y at a
point x from a given tabular points by Newton’s Forward and
backward difference Interpolation formulae for equally
spaced points.
•To write a program in order to find out the value of y at a
point x from a given tabular points by Lagrange’s
interpolation formula for equally or not equally spaced points.
•To write a program in order to find out the value of x at a
point y from a given tabular data by Inverse Lagrange’s
interpolation formula.

6. 4/10/2017 6
Theory:
Interpolation with evenly spaced data points by Newton’s forward and backward
difference formulae.
For the points at the beginning of Tabular data Let there are n+1 number of data points,
are given. When values of x are at equal distance and the value of x, for which the value
of y is to be determined, is at the beginning of the given data table then use Newton’s
forward difference interpolation Formula to find the polynomial y, which is,
….(1)
Where,
h=difference between two successive values of x.
The values can be found from the following forward and back-word difference Table (Table-1
and 2).
),)........(,(),,( 1100 nn yxyxyx
00
3
0
2
)!(
)1)........(2)(1(
............
!3
)2)(1(
!2
)1(
)( y
n
npppp
y
ppp
y
pp
ypyxy n
oon 






phxx  0

7. Table-1:Forward difference Table(n=5)

8. 4/10/2017MATLAB by Tajim 8
Table-2: Backward difference Table (n=5)
and relation between forward and backward elements

9. 4/10/2017MATLAB by Tajim 9
Example 1

10. 4/10/2017MATLAB by Tajim 10
Example 1

11. 4/10/2017MATLAB by Tajim 11
Example 2

12. 4/10/2017MATLAB by Tajim 12
Example 2

13. 4/10/2017MATLAB by Tajim 13
Example 2

14. 4/10/2017MATLAB by Tajim 14

15. 4/10/2017MATLAB by Tajim 15
MATLAB code for
Newton's Forward and
back-word Interpolation
method.

16. 4/10/2017MATLAB by Tajim 16
Code of problem 1

17. 4/10/2017MATLAB by Tajim 17
Output of problem 1
1
2
3

18. 4/10/2017MATLAB by Tajim 18
Code of problem 2

19. Output of problem 2

20. 4/10/2017MATLAB by Tajim 20
End of
LECTURE
Eight
Thank You .
References: MSK and MMS sir’s lecture.
Reference Book:
1)Introductory Methods of Numerical Analysis: by S.S. Sastry.
2)Numerical Methods -Gerald/Wheetley