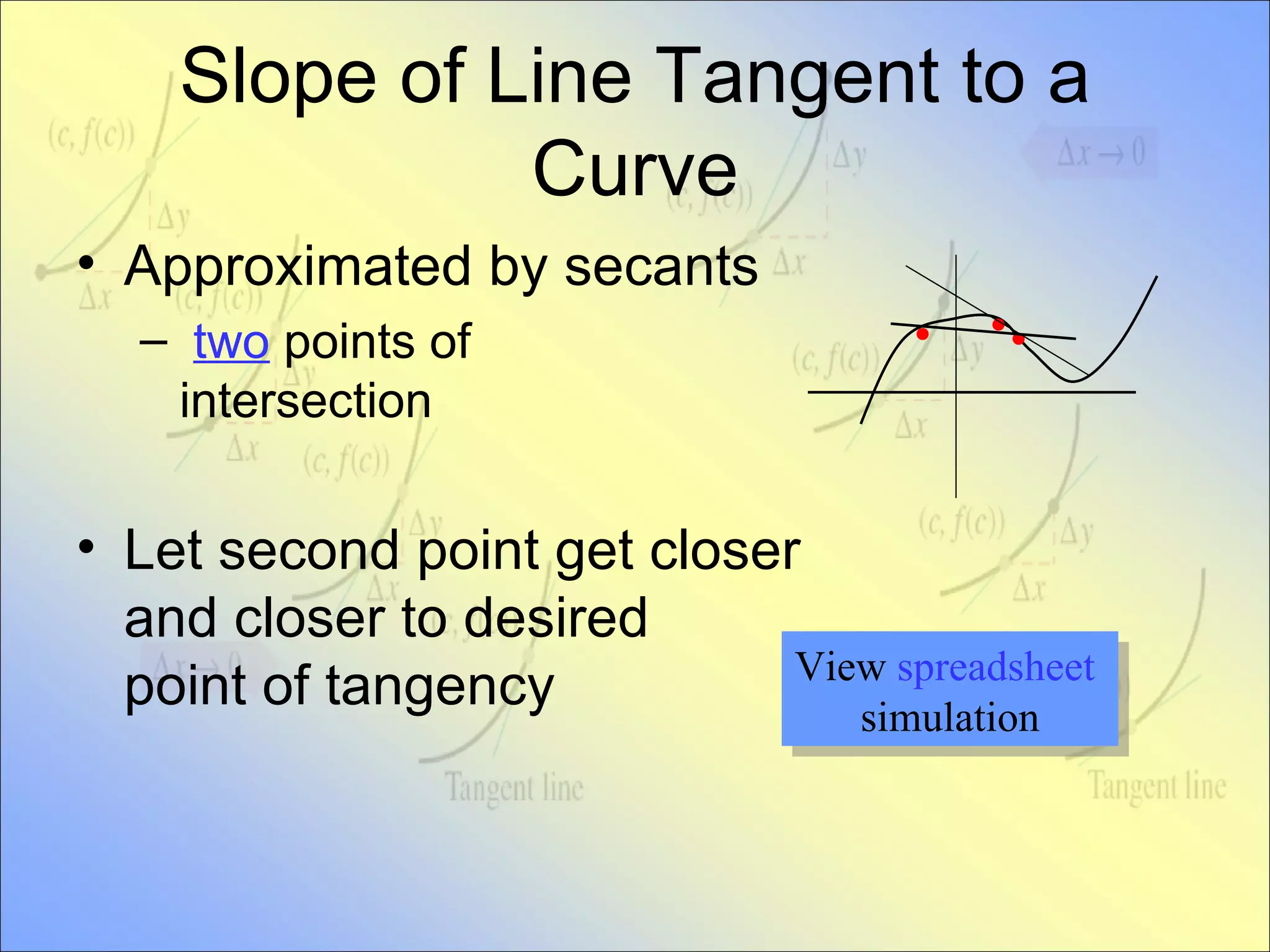
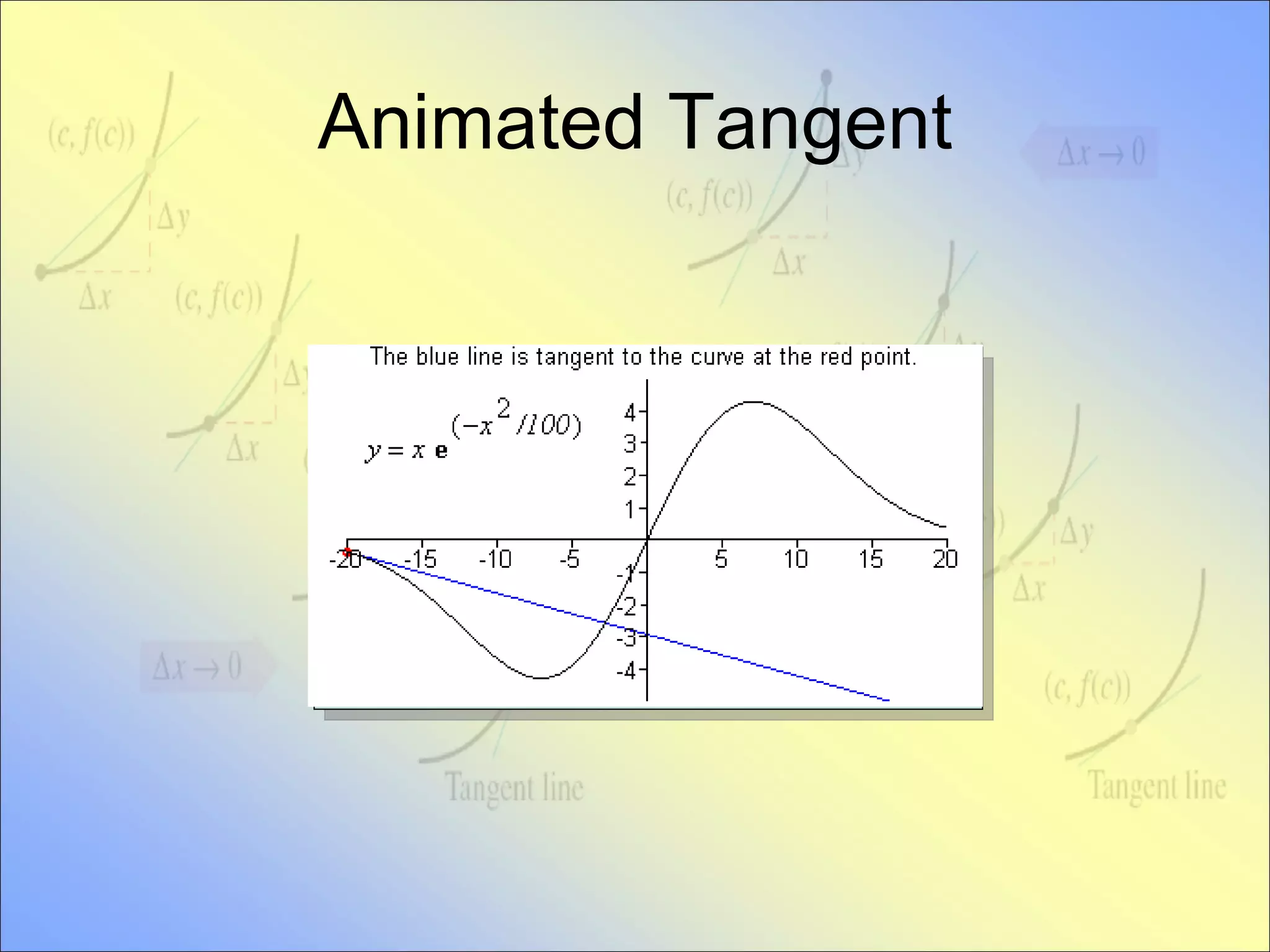
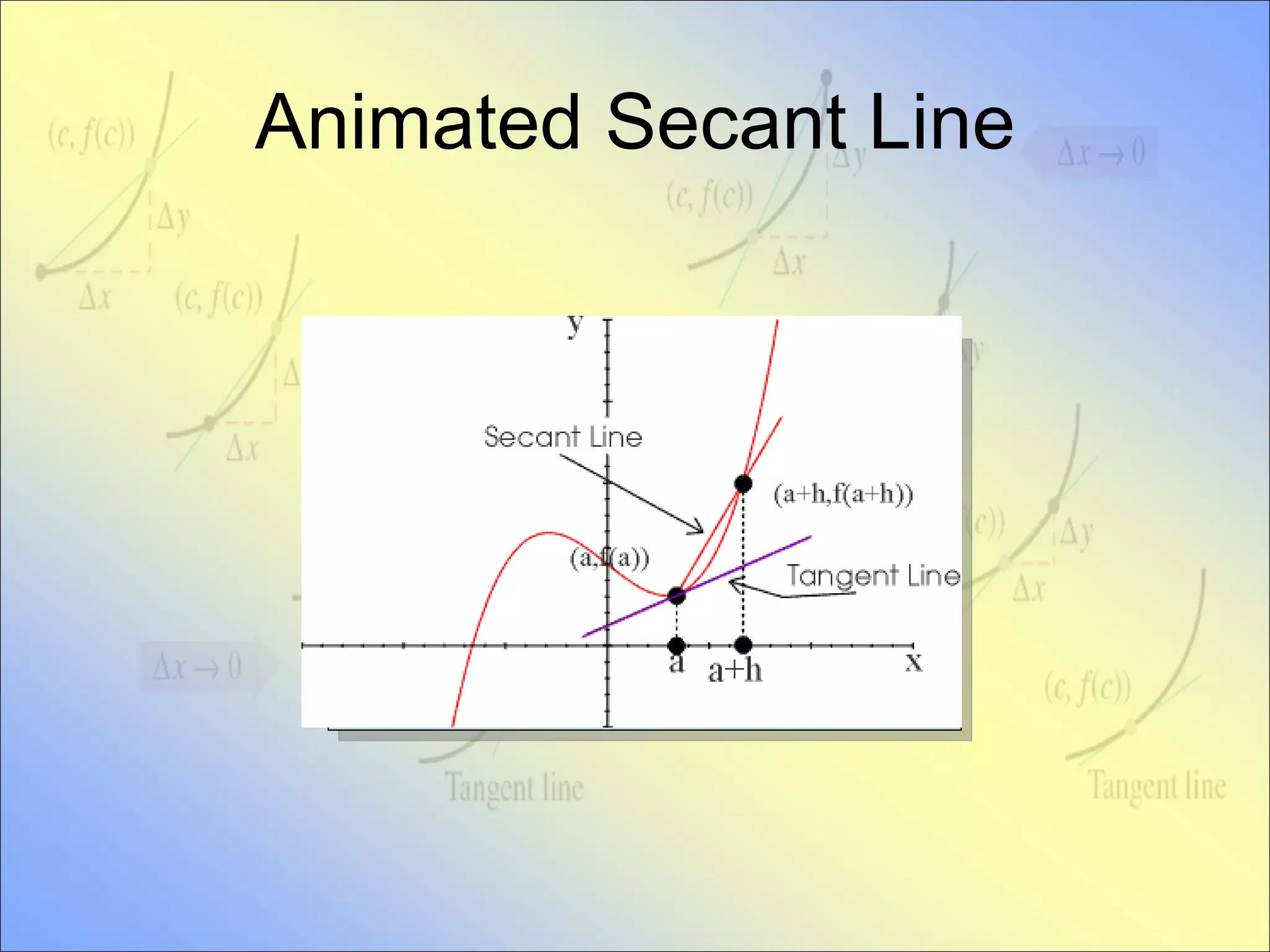
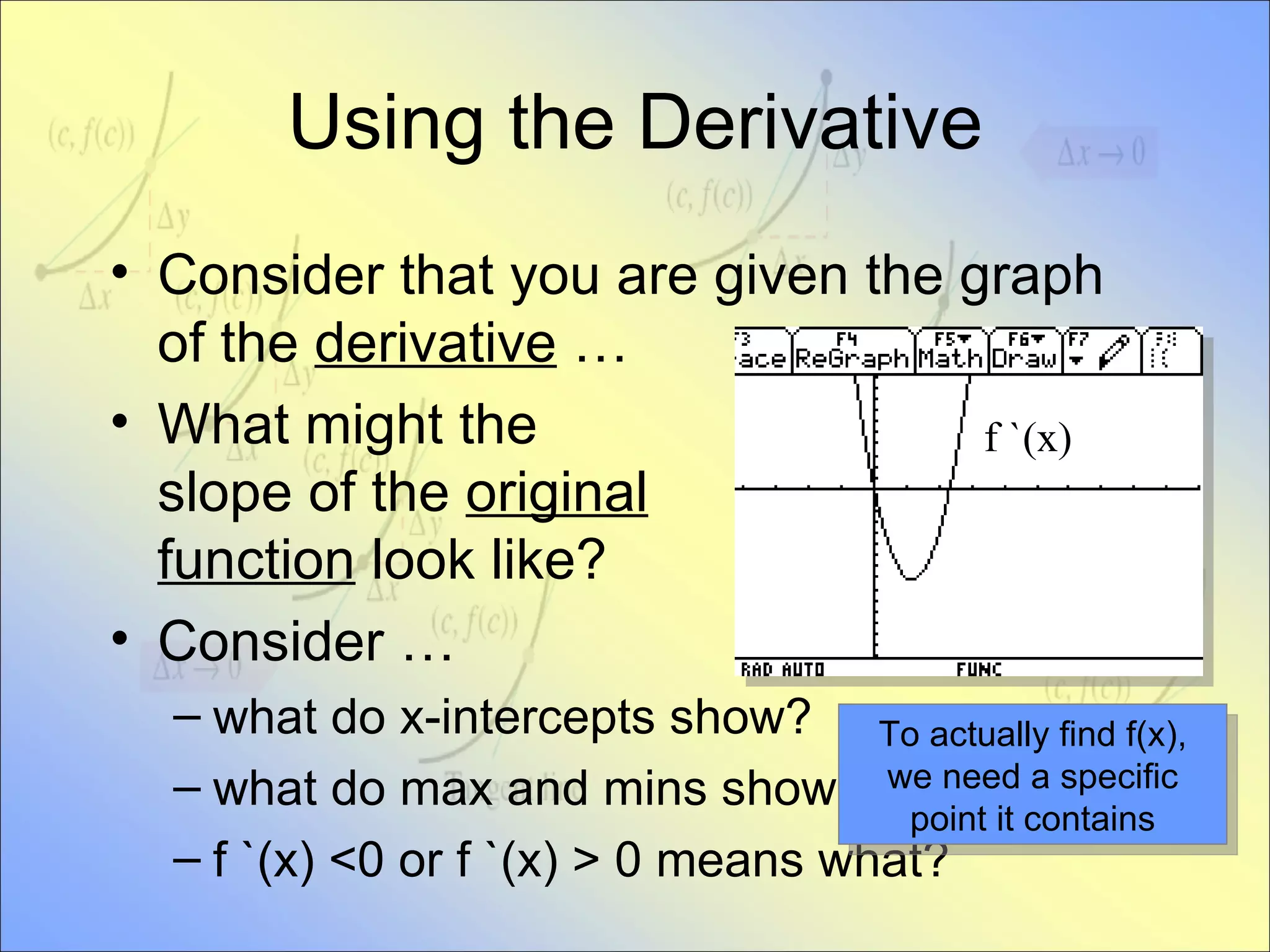
This document provides an introduction to the concept of the tangent line and derivative. It defines the tangent line as the line that intersects a curve at exactly one point. It discusses how to approximate the slope of a tangent line using secant lines and taking the limit as the second point approaches the point of tangency. The derivative is defined as the formula that gives the slope of the tangent line at any point on a curve. It provides examples of using calculators to calculate derivatives and discusses how the graph of a derivative relates to properties of the original function such as maxima, minima and x-intercepts.

1. The Derivative and the Tangent Line Problem Lesson 3.1

2. Definition of Tan-gent

3. Tangent Definition From geometry a line in the plane of a circle intersects in exactly one point We wish to enlarge on the idea to include tangency to any function, f(x)

4. Slope of Line Tangent to a Curve Approximated by secants two points of intersection Let second point get closer and closer to desired point of tangency • View spreadsheet simulation • •

5. Animated Tangent

6. Slope of Line Tangent to a Curve Recall the concept of a limit from previous chapter Use the limit in this context • •

7. Definition of a Tangent Let Δ x shrink from the left

8. Definition of a Tangent Let Δ x shrink from the right

9. The Slope Is a Limit Consider f(x) = x 3 Find the tangent at x 0 = 2 Now finish …

10. Animated Secant Line

11. Calculator Capabilities Able to draw tangent line Steps Specify function on Y= screen F5-math, A-tangent Specify an x (where to place tangent line) Note results

12. Difference Function Creating a difference function on your calculator store the desired function in f(x) x^3 -> f(x) Then specify the difference function (f(x + dx) – f(x))/dx -> difq(x,dx) Call the function difq(2, .001) Use some small value for dx Result is close to actual slope

13. Definition of Derivative The derivative is the formula which gives the slope of the tangent line at any point x for f(x) Note: the limit must exist no hole no jump no pole no sharp corner A derivative is a limit !

14. Finding the Derivative We will (for now) manipulate the difference quotient algebraically View end result of the limit Note possible use of calculator limit ((f(x + dx) – f(x)) /dx, dx, 0)

15. Related Line – the Normal The line perpendicular to the function at a point called the “normal” Find the slope of the function Normal will have slope of negative reciprocal to tangent Use y = m(x – h) + k

16. Using the Derivative Consider that you are given the graph of the derivative … What might the slope of the original function look like? Consider … what do x-intercepts show? what do max and mins show? f `(x) <0 or f `(x) > 0 means what? To actually find f(x), we need a specific point it contains f `(x)

17. Derivative Notation For the function y = f(x) Derivative may be expressed as …

18. Assignment Lesson 3.1 Page 123 Exercises: 1 – 41, 63 – 65 odd