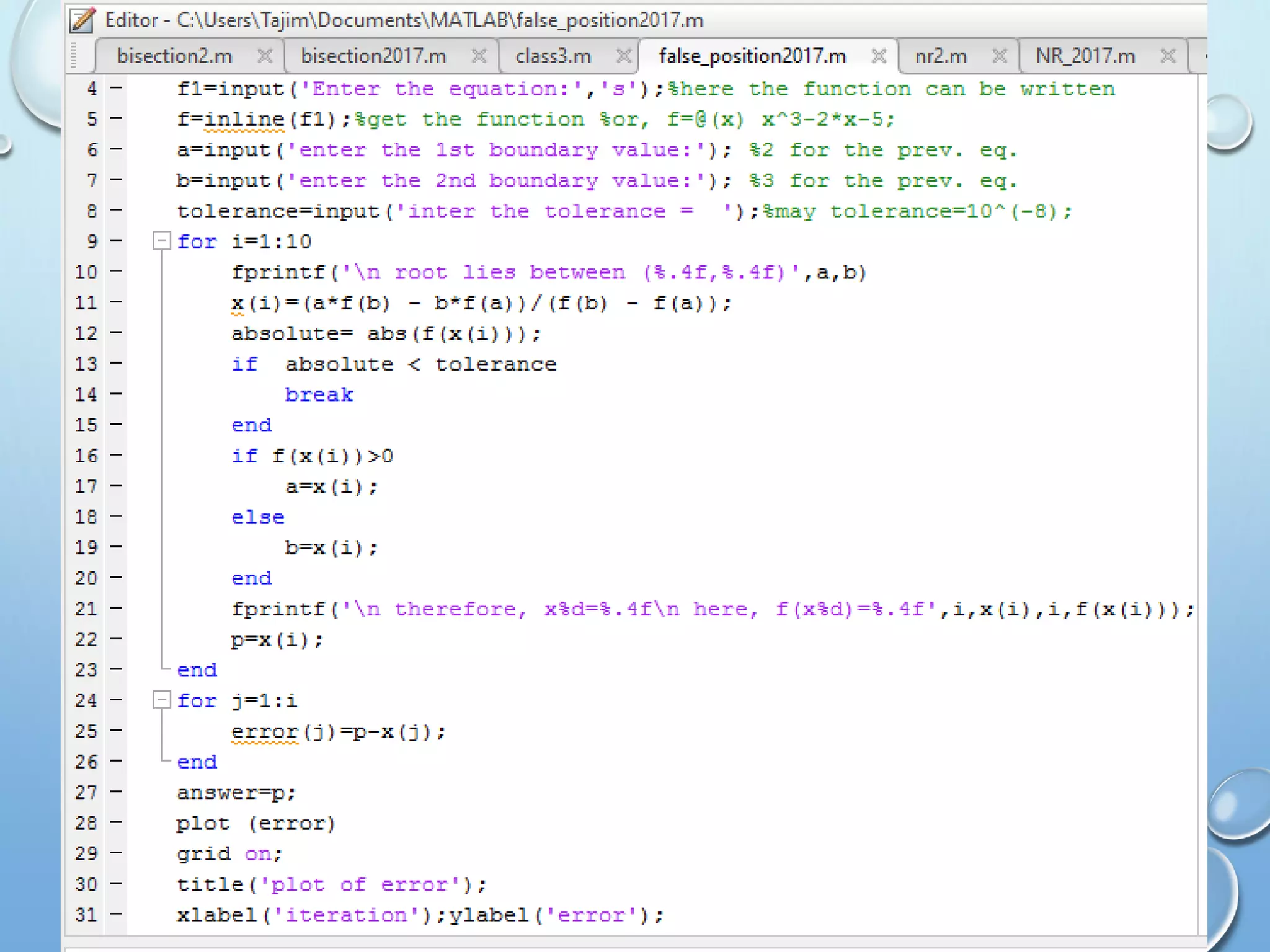
The document details the 'Regula Falsi' or false position method for finding roots of equations using MATLAB, highlighting its advantages over the bisection method. It explains the theoretical background and practical application through an example, demonstrating how the method converges to a root. Additionally, it provides several equations to be solved using the method and includes MATLAB code and outputs for illustration.

1. IT-2210 : Computational
mathematics LAB with
MATLAB
4/10/2017MATLAB by Tajim 1

2. Lecture 7: MATLAB – Regula falsi
or False position method.
4/10/2017MATLAB by Tajim 2

3. 4/10/2017MATLAB by Tajim 3
Regula falsi or False position method.
False position method and regula falsi method are two early, and still
current, names for a very old method for solving an equation in one
unknown.
The Converge process in the bisection method is very slow. Because the
interval between x1 and x2 is divided into two equal half and calculate
the first approximate value[𝑥0=𝑥1+𝑥22]. Actually it is used only to
decide the next smaller interval. But a better approximation can be
obtained by taking a straight line both the two end points. Thus the point
of intersection of this line with x axis (x0) gives an improved estimate of
the root and is called the false position of the root. The value of this point
(x0) and its function is taking as the initial guesses.

4. 4/10/2017MATLAB by Tajim 4
Regula falsi or False position method.
In scientific and engineering work, a frequently occurring
problem is to find the roots of equations of the form y=f(x)=0,
i.e finding the value of x where the value of y=f(x) is equal to
0. In quadratic, cubic or a biquadratic equations, algebraic
formulae are available for expressing the roots in terms of co-
efficient. But in the case, where f(x) is a polynomial of higher
degree or an expression involving transcendental functions, the
algebraic methods are not applicable and the help of
numerical method must be taken to find approximate roots.

5. 4/10/2017MATLAB by Tajim 5
Objectives of this experiment
To write a program in order to find
out the roots of a nonlinear equation
by the method of False Position in
matlab.

6. 4/10/2017MATLAB by Tajim 6
Theory

7. 4/10/2017MATLAB by Tajim 7
Theory Cont……
-10 -5 0 5 10 15 20 25 30
-200
-100
0
100
200
300
400
500
x
y=f(x)
Fig.1
B[x1,f(x1)]
A[x0,f(x0)]
x2 x3 x4
real root, x
x0 x1

8. 4/10/2017MATLAB by Tajim 8
Theory Cont……

9. 4/10/2017MATLAB by Tajim 9
Ex-1: Find the positive root of 𝑥3=2𝑥-5 by false position method.
Solution: let 𝑓(𝑥)= 𝑥3−2𝑥-5……………………..(1)
Here, 𝑓(2)=8−9=−1<𝟎; 𝑓(3)=27−6−5=16>𝟎
So the root lies between 2 and 3. So, a=2; b=3
Now Regula falsi method: 𝒙𝟎=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎) =
2𝑓(3)−3𝑓(2)𝑓(3)−𝑓(2)=(2∗16−3∗(−1))16−(−1)=𝟐.𝟎𝟓𝟖𝟖𝟐𝟒
Now from (1) we can write: 𝑓(𝑥0)=(𝑥0)3−2𝑥0+5=(𝟐.𝟎𝟓𝟖𝟖𝟐𝟒)3−2∗𝟐.𝟎𝟓𝟖𝟖𝟐𝟒+5=
−0.390795<0
So the root lies between 𝟐.𝟎𝟓𝟖𝟖𝟐𝟒 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟓𝟖𝟖𝟐𝟒,𝑏=3]
𝒙𝟏=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=2.058824∗𝑓(3)−3𝑓(2.058824)𝑓(3)−𝑓(2.058824)=𝟐.𝟎𝟖𝟏𝟐𝟔𝟒
From (1) we can write:
𝑓(𝑥1)=(𝑥1)3−2𝑥1+5=(𝟐.𝟎𝟖𝟏𝟐𝟔𝟒)3−2∗𝟐.𝟎𝟖𝟏𝟐𝟔𝟒+5= −0.147200<0
So the root lies between 𝟐.𝟎𝟖𝟏𝟐𝟔𝟒 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟖𝟏𝟐𝟔𝟒,𝑏=3]
𝒙𝟐=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟖𝟏𝟐𝟔𝟒∗𝑓(3)−3𝑓(𝟐.𝟎𝟖𝟏𝟐𝟔𝟒)𝑓(3)−𝑓(𝟐.𝟎𝟖𝟏𝟐𝟔𝟒)=𝟐.𝟎𝟖𝟗𝟔𝟑𝟗

10. 4/10/2017MATLAB by Tajim 10
Ex-1: cont………………….
From (1) we can write: 𝑓(𝑥2)=(𝑥2)3−2𝑥2+5=(𝟐.𝟎𝟖𝟗𝟔𝟑𝟗)3−2∗𝟐.𝟎𝟖𝟗𝟔𝟑𝟗+5= −0.054679<0
So the root lies between 𝟐.𝟎𝟖𝟗𝟔𝟑𝟗 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟖𝟗𝟔𝟑𝟗,𝑏=3]
𝒙𝟑=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟖𝟗𝟔𝟑𝟗∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟖𝟗𝟔𝟑𝟗)𝑓(3)−𝑓(𝟐.𝟎𝟖𝟗𝟔𝟑𝟗)=𝟐.𝟎𝟗𝟐𝟕𝟒
From (1) we can write: 𝑓(𝑥3)=(𝑥3)3−2𝑥3+5=(𝟐.𝟎𝟗𝟐𝟕𝟒)3−2∗𝟐.𝟎𝟗𝟐𝟕𝟒+5= −0.020198<0
So the root lies between 𝟐.𝟎𝟗𝟐𝟕𝟒 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟗𝟐𝟕𝟒,𝑏=3]
𝒙𝟒=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟐𝟕𝟒∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟐𝟕𝟒)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟐𝟕𝟒)=𝟐.𝟎𝟗𝟑𝟖𝟖𝟒
From (1) we can write: 𝑓(𝑥4)=(𝑥4)3−2𝑥4+5=(𝟐.𝟎𝟗𝟑𝟖𝟖𝟒)3−2∗𝟐.𝟎𝟗𝟑𝟖𝟖𝟒+5= −0.007448<0
So the root lies between 𝟐.𝟎𝟗𝟑𝟖𝟖𝟒 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟗𝟑𝟖𝟖𝟒,𝑏=3]
𝒙𝟓=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟑𝟖𝟖𝟒∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟑𝟖𝟖𝟒)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟑𝟖𝟖𝟒)=𝟐.𝟎𝟗𝟒𝟑𝟎𝟔
From (1) we can write: 𝑓(𝑥5)=(𝑥5)3−2𝑥5+5=(𝟐.𝟎𝟗𝟒𝟑𝟎𝟔)3−2∗𝟐.𝟎𝟗𝟒𝟑𝟎𝟔+5= −0.002740<0
So the root lies between 𝟐.𝟎𝟗𝟒𝟑𝟎𝟔 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟗𝟒𝟑𝟎𝟔,𝑏=3]
𝒙𝟔=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟒𝟑𝟎𝟔∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟒𝟑𝟎𝟔)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟒𝟑𝟎𝟔)=𝟐.𝟎𝟗𝟒𝟒𝟔𝟏

11. 4/10/2017MATLAB by Tajim 11
Ex-1: cont………………….
𝒙𝟔=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟒𝟑𝟎𝟔∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟒𝟑𝟎𝟔)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟒𝟑𝟎𝟔)=𝟐.𝟎𝟗𝟒𝟒𝟔𝟏
From (1) we can write: 𝑓(𝑥6)=(𝑥6)3−2𝑥6+5=(𝟐.𝟎𝟗𝟒𝟒𝟔𝟏)3−2∗𝟐.𝟎𝟗𝟒𝟒𝟔𝟏+5= −0.0010098<0
So the root lies between 𝟐.𝟎𝟗𝟒𝟒𝟔𝟏 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟗𝟒𝟒𝟔𝟏,𝑏=3]
𝒙𝟕=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟒𝟒𝟔𝟏∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟒𝟒𝟔𝟏)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟒𝟒𝟔𝟏)=𝟐.𝟎𝟗𝟒𝟓𝟏
From (1) we can write: 𝑓(𝑥7)=(𝑥7)3−2𝑥7+5=(𝟐.𝟎𝟗𝟒𝟓𝟏)3−2∗𝟐.𝟎𝟗𝟒𝟓𝟏+5= −0.0003914<0
So the root lies between 𝟐.𝟎𝟗𝟒𝟓𝟏 𝑎𝑛𝑑 3 ⇒[𝑎=𝟐.𝟎𝟗𝟒𝟓𝟏,𝑏=3]
𝒙𝟖=𝑎𝑓(𝑏)−𝑏𝑓(𝑎)𝑓(𝑏)−𝑓(𝑎)=𝟐.𝟎𝟗𝟒𝟓𝟏∗𝑓(3)−3∗𝑓(𝟐.𝟎𝟗𝟒𝟓𝟏)𝑓(3)−𝑓(𝟐.𝟎𝟗𝟒𝟓𝟏)=𝟐.𝟎𝟗𝟒𝟓𝟑
∴𝒙𝟕=𝒙𝟖=𝟐.𝟎𝟗𝟒𝟓
Hence the required root is : 𝟐.𝟎𝟗𝟒𝟓

12. 4/10/2017MATLAB by Tajim 12
MATLAB code for
Regula falsi or False
position method.

13. 4/10/2017MATLAB by Tajim 13

14. 4/10/2017MATLAB by Tajim 14
MATLAB output for
Newton Raphson
method
For the equation: f(x) = x^3-2*x-5

15. 4/10/2017MATLAB by Tajim 15
MATLAB output of false position method (Graph)

16. 4/10/2017MATLAB by Tajim 16
MATLAB output of N-R method (Console)
For the equation: f(x) = x^3-2*x-5

17. 4/10/2017MATLAB by Tajim 17
Now solve with MATLAB and show the output in console and
Graph for a positive root of the following equation by using
Regula Falsi Method.
1. 𝑥3−4𝑥−1=0 ⇾𝑓(1)=−2<0;𝑓(0)=1>0 [𝑎=0;𝑏=1]
2. 3𝑥−cos𝑥−1=0 ⇾𝑓(0.6)=−0.0253<0;𝑓(0.61)=0.0104>0
[𝑎=0.6;𝑏=0.61]
3. 𝑥3−2𝑥−5=0⇾𝑓(2)=−3<0;𝑓(3)=13>0 [𝑎=2;𝑏=3]
4. 𝑥3−5𝑥+3=0⇾𝑓(1)=−1<0;𝑓(2)=1>0 [𝑎=1;𝑏=2]
5. 𝑥log10𝑥−1.2=0⇾𝑓(2)=−0.597940<0;𝑓(3)=0.23136>0 [𝑎=2;𝑏=3]
6. x2−log𝑒𝑥−12=0⇾𝑓(3)=−4.0986<0;𝑓(4)=2.6137>0 [𝑎=3;𝑏=4]

18. 4/10/2017MATLAB by Tajim 18
End of
LECTURE
seven
Thank You .
References: MSK and MMS sir’s
lecture.