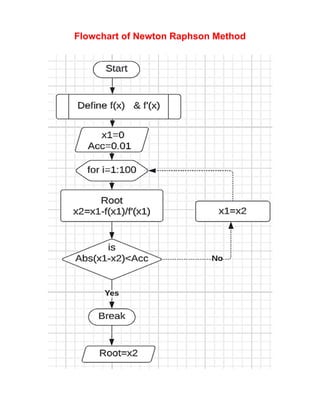
This document discusses numerical methods for solving engineering problems. It introduces numerical methods as ways to find approximate solutions to complex problems that cannot be solved analytically. Bisection and Newton-Raphson methods are described for finding roots of equations. Examples are provided to demonstrate applying the bisection method to find roots of polynomial and transcendental equations. The Newton-Raphson method is also demonstrated for finding roots. Flowcharts and MATLAB programs for implementing the methods are included.

1. Sanjivani College of Engineering Kopargaon
Department of Mechanical Engineering
-----------------------------------------------------------------------
Class: SY Subject: Numerical Methods
About Numerical Methods (NMs)
 Analytical methods are the most difficult ones, providing
exact solutions, but they become hard to use for complex
problems in practical engineering applications.
 In such cases Numerical methods are important to give
approximate solutions by satisfying certain accuracy.
 NMs use arithmetic operators to solve engineering based
mathematical problems.
 So Engineers must acquire a working knowledge of NMs
and also efficient programming skill for real life
applications.
Steps in NMs
1. Selection of proper NM
2. Algorithm ( Procedural steps)
3. Flowchart ( Graphical representation of procedural steps)
4. Programming (MatLAB)
5. Execution of Program
D.P.Bhaskar
Dept of Mech Engg

2. Unit 1 Roots of Equation
Polynomial Equation: Function, f x 3x2 9 0 f x 3x2 4x‐8 0 etc.
Transcendental equation. Function, f x 3x2 sin x ex 0
If x contains trigonometric, logarithmic or exponential functions, then 0 is called a
transcendental equation.
Root of Equations:
 Function, f x 3x2 sin x ex 0
 Root of equation means finding value of x to satisfy f x 0.
 It means f x value will be zero for certain x. That is also called as zero of equation.
Numerical Methods to compute Root of Equations:
 Bisection Method Half interval Search Method
 Newton Raphson Method Tangent Method
Bisection Method
The bisection method is a root‐finding method that applies to any continuous function for
which one knows two values with opposite signs. The method consists of
repeatedly bisecting the interval defined by these values and then selecting the subinterval in
which the function changes sign, and therefore must contain a root.
Steps in Bisection Method
Step1 Initial Guesses X1 & X2 such a that f X1 & f X2 must be of opposite sign.
Step2 Root: X3 X1 X2 /2
Step3 Iterate this Root till Acc is achieved.
If |x1-x2 | X3 is final root Stop Break
Else if f X1 * f X3 is ve X1 ←X3
f X1 * f X3 is ‐ ve X2 ←X3
Step 2 and Iterate …..

3. Q1 Find the root of f x x2 ‐ 3. By Bisection Method Let Acc 0.01.
Solution
Initial Guesses
X1 1 f X1 ‐2
X2 2 f X2 1 Are of opposite sign.
Result Table
Procedure:
If |x1-x2 | X3 is final root Stop
Else if f X1 * f X3 is ve X1 ←X3
f X1 * f X3 is ‐ ve X2 ←X3
----------------------------------------------------------------------------------------------------
I x1 x2 x3 |x1‐x2 | f x1 *f x3
---------------------------------------------------------------------------------------------------
1 1. 2. 1.5 1. 1.5
2 1.5 2. 1.75 0.5 ‐0.04
3 1.5 1.75 1.625 0.25 0.2
4 1.625 1.75 1.6875 0.125 0.05
5 1.6875 1.75 1.7188 0.0625 0.007
6 1.7188 1.75 1.7344 0.0312 ‐0.0004
7 1.7188 1.7344 1.7266 0.0156 0.0009
8 1.7266 1.7344 1.7305 0.0078 0.0001
------------------------------------------------------------------------------------------------------
As |x1-x2 | .
Q2 Find the root of x ‐ e‐x 0 Let Acc 0.01. y Bisection Method
Solution
Initial Guesses
X1 0 f X1 ‐ve
X2 1 f X2 ve Are of opposite sign.
Result Table
Procedure:
If |x1-x2 | X3 is final root Stop
Else if f X1 * f X3 is ve X1 ←X3
f X1 * f X3 is ‐ ve X2 ←X3
---------------------------------------------------------------------------
I x1 x2 x3 |x1‐x2 | f x1 *f x3
---------------------------------------------------------------------------
1 0 1 0.5 1 0.1
2 0.5 1 0.75 0.5 ‐0.02
3 0.5 0.75 0.625 0.25 ‐0.009
4 0.5 0.625 0.5625 0.125 0.0008
5 0.5625 0.625 0.5938 0.0625 ‐0.0003
6 0.5625 0.5938 0.5781 0.0312 ‐0.0001
7 0.5625 0.5781 0.5703 0.0156 ‐0.00004
8 0.5625 0.5703 0.5664 0.0078 0.00001
-------------------------------------------------------------------------
As |x1-x2 | .

4. Q3 Find the root of f x x3‐cos2 x . Bisection Method. Acc 0.01.
Solution
Initial Guesses
X1 1 f X1 ‐1
X2 2 f X2 0.7081 Are of opposite sign.
Result Table
Procedure:
If |x1-x2 | X3 is final root Stop
Else if f X1 * f X3 is ve X1 ←X3
f X1 * f X3 is ‐ ve X2 ←X3
----------------------------------------------------------------------------------------------------
I x1 x2 x3 |x1‐x2 | f x1 *f x3
---------------------------------------------------------------------------------------------------
1 0 1 0.5 1 0.006
2 0.5 1. 0.75 0.5 0.07
3 0.75 1. 0.875 0.25 ‐0.02
4 0.75 0.875 0.8125 0.1250 ‐0.007
5 0.75 0.8125 0.7812 0.0625 0.003
6 0.7812 0.8125 0.7969 0.0312 ‐0.0004
7 0.7812 0.7969 0.7891 0.0156 0.0001
8 0.7891 0.7969 0.7930 0.0078 ‐0.00003
------------------------------------------------------------------------------------------------------
As |x1-x2 | .

5. A flowchart is a picture of the separate steps of a process in sequential order.
Flowchart of Bisection Method

6. Simple program of Bisection Method ( Accuracy input)
clc
clear all
f=inline('x‐cos(x)'); x1=0; x1=1; acc=0.001;
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
for i=1:100
x3=(x1+x2)/2;
b=abs(x1‐x2); c=(f(x1)*f(x3));
if(b<acc) break
else if(c>0) x1=x3; else x2=x3; end
end
end
fprintf('n Root=%f',x3);
Simple program of Bisection Method ( Number of iteration input e.g i=10)
clc
clear all
f=inline('x‐cos(x)'); x1=0; x1=1;
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
for i=1:10
x3=(x1+x2)/2;
c=(f(x1)*f(x3));
if(c>0) x1=x3; else x2=x3;
end
end
fprintf('n Root=%f',x3);

7. Program of Bisection Method ( Acc inout & checking for correct x1 & x2 and printing
entire Table result)
clc
clear all
f=inline('x‐cos(x)'); acc=0.001;
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
for i=1:100
x1=input('Enter new x1');
x2=input('Enter new x2');
if(f(x1)*f(x2)<0) break
end
end
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐n');
fprintf('I x1 x2 x3 Acc Error)');
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐');
for i=1:100
x3=(x1+x2)/2;
b=abs(x1‐x2); c=(f(x1)*f(x3));
fprintf('n%d %.4f %.4f %.4f %.4f %.4f ',i,x1,x2,x3,b,c);
if(b<acc) break
else if(c>0) x1=x3; else x2=x3; end
end
end
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐');
fprintf('n Root=%f',x3);
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐

8. Newton’s Raphson method
Is a method for finding successively better approximations to the roots (or zeroes) of a real-
valued function.
The Newton–Raphson method in one variable is implemented as follows:
Given a function ƒ(x), and its derivative ƒ'(x), we begin with a first guess x1 for a root of the
function f(x). Provided the function satisfies all the assumptions made in the derivation of the
formula, a better approximation x2 is:
Root Formula
′
The process is repeated until a
sufficiently accurate value is
reached.
For correct Initial Guess(x1):
| f ’ X1 | | f X1 |
Initial Guess is Correct

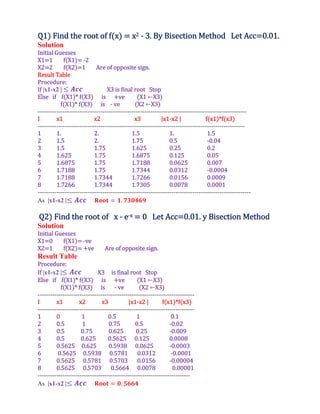
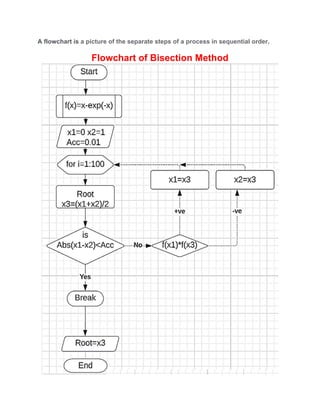
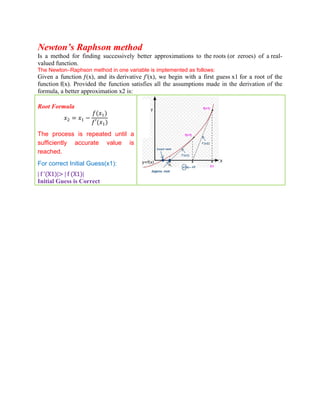
9. Q1 Find the root of f x excos x ‐1.2 . Newton Raphson Method.
Acc 0.001.
Given
f x excos x ‐1.2 Function
f ’ x ex cos x ‐sin x Tangent or Slope or Derivative
Solution
Initial Guess
X1 1 And | f X1 | 0.2687 | f ’ X1 | 0.8187
Since | f ’ X1 | | f X1 | Initial Guess is Correct
Step 1 Root
′
Step2 If |x1-x2 | X2 is final root Stop
Else X1 ←X2 and goto Step 1
Result table
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
I x1 f x1 fd x1 x2 |x1‐x2 |
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
1 1. 0.2687 ‐0.8187 1.3282 0.3282
2 1.3282 ‐0.2934 ‐2.7571 1.2218 0.1064
3 1.2218 ‐0.0397 ‐2.0284 1.2023 0.0196
4 1.2023 ‐0.0012 ‐1.9054 1.2016 0.0006
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
As |x1-x2 | .
Q1* Find the root of f x excos x ‐1.2 . Newton Raphson Method.
Acc 0.001. Initial Guess is x1 2
| f ’ X1 | | f X1 | ]
Means no need to check

10. Q2 Find the root of f x x3‐cos2 x . Newton Raphson Method.
Acc 0.001.
Given
f x x3‐cos2 x Function
f ’ x 3x2 sin 2x Tangent or Slope or Derivative
Solution
Initial Guess
X1 1 And | f X1 | 0.7081 | f ’ X1 | 3.9093
Since | f ’ X1 | | f X1 | Initial Guess is Correct
Step 1 Root
′
Step2 If |x1-x2 | X2 is final root Stop
Else X1 ←X2 and goto Step 1
Result table
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
I x1 f x1 fd x1 x2 |x1‐x2 |
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
1 1. 0.7081 3.9093 0.8189 0.1811
2 0.8189 0.0826 3.0094 0.7914 0.0274
3 0.7914 0.0018 2.8791 0.7908 0.0006
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
As |x1-x2 | .
Q2* Find the root of f x x3‐cos2 x . For 3 Iteartions
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
I x1 f x1 fd x1 x2
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
1 1. 0.7081 3.9093 0.8189
2 0.8189 0.0826 3.0094 0.7914
3 0.7914 0.0018 2.8791 0.7908
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
. No need to check whether Acc is achieved just complete 3 iterations

11. Flowchart of Newton Raphson Method

12. Program (Simple) %Newton Raphson Method
clc
clear all
f=inline('x-exp(-x)');
fd=inline('1+exp(-x)');
acc=0.0001; x1=1;
for i=1:100
x2=x1-f(x1)/fd(x1);
b=abs(f(x2));
if(b<acc) fprintf('n Root=%f',x2); break
else x1=x2;
end
end
Program (Table) %Newton Raphson Method
clc
clear all
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
f=inline('x.^3‐cos(x)*cos(x)');
fd=inline('2*cos(x)*sin(x) + 3*x.^2');
acc=0.001; x1=1;
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐n');
fprintf('I x1 f(x1) fd(x1) x2 Acc');
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐');
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
abs(f(x1))
abs(fd(x1))
for i=1:100
x2=x1‐f(x1)/fd(x1);
b=abs(x1‐x2);
fprintf('n%d %.4f %.4f %.4f %.4f %.4f',i,x1, f(x1), fd(x1),x2,b);
if(b <acc) break
else x1=x2;
end
end
%‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
fprintf('n‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐');
fprintf('n Root=%f',x2);