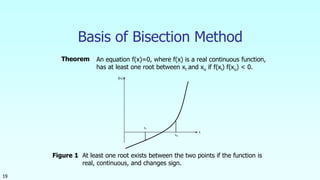
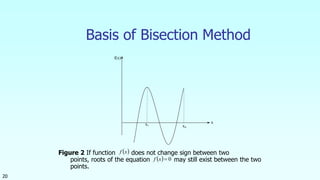
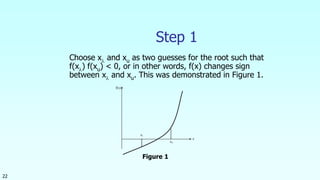
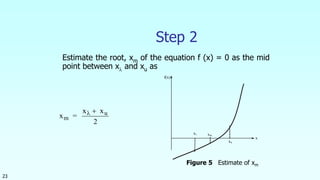
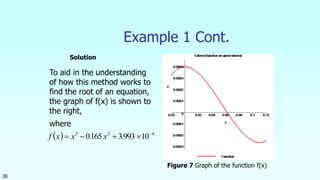
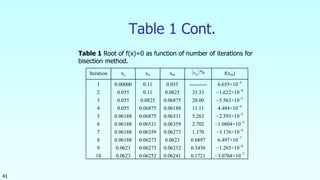
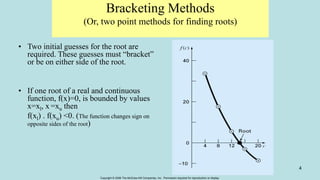
This document discusses the bisection method for finding roots of equations. It begins by introducing the bisection method and explaining that it uses an initial interval that brackets a root to successively narrow down the interval containing the root. It then provides the steps of the bisection method algorithm. Finally, it includes an example of applying the bisection method to find the depth at which a floating ball is submerged. Over 10 iterations, the method converges on a root of 0.06252 within the specified error tolerance.

1. 1
Numerical Method
Lecture No.02
Rubya Afrin
Lecturer
Northern University of Business and Technology

2. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
2
Roots of Equations
•Why?
•But
a
acbb
xcbxax
2
4
0
2
2 


?0sin
?02345


xxx
xfexdxcxbxax

3. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
3
Nonlinear Equation
Solvers
Bracketing Graphical Open Methods
Bisection
False Position
(Regula-Falsi)
Newton Raphson
Secant
All Iterative

4. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
4
Bracketing Methods
(Or, two point methods for finding roots)
• Two initial guesses for the root are
required. These guesses must “bracket”
or be on either side of the root.
• If one root of a real and continuous
function, f(x)=0, is bounded by values
x=xl, x =xu then
f(xl) . f(xu) <0. (The function changes sign on
opposite sides of the root)

5. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
5
Figure 5.2
No answer (No root)
Nice case (one root)
Oops!! (two roots!!)
Three roots( Might
work for a while!!)

6. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
6
Figure 5.3
Two roots( Might
work for a while!!)
Discontinuous
function. Need
special method

7. Copyright © 2006 The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
7
Figure 5.4a
Figure 5.4b
Figure 5.4c
MANY-MANY roots. What do we
do?
f(x)=sin 10x+cos 3x

8. The Bisection Method
8

9. Introduction
• Bisection Method:
• Bisection Method = a numerical method in
Mathematics to find a root of a given function
9

10. Introduction (cont.)
• Root of a function:
• Root of a function f(x) = a value a such that:
• f(a) = 0
10

11. Introduction (cont.)
• Example:
Function: f(x) = x2 - 4
Roots: x = -2, x = 2
Because:
f(-2) = (-2)2 - 4 = 4 - 4 = 0
f(2) = (2)2 - 4 = 4 - 4 = 0
11

12. A Mathematical Property
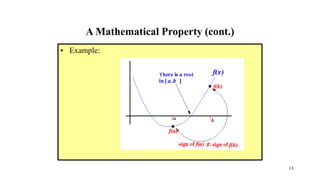
• Well-known Mathematical Property:
• If a function f(x) is continuous on the interval [a..b] and
sign of f(a) ≠ sign of f(b), then
• There is a value c ∈ [a..b] such that: f(c) =
0 I.e., there is a root c in the interval [a..b]
12

13. A Mathematical Property (cont.)
• Example:
13

14. The Bisection Method
• The Bisection Method is a successive approximation method
that narrows down an interval that contains a root of the
function f(x)
• The Bisection Method is given an initial interval [a..b] that
contains a root (We can use the property sign of f(a) ≠ sign of
f(b) to find such an initial interval)
• The Bisection Method will cut the interval into 2 halves and
check which half interval contains a root of the function
• The Bisection Method will keep cut the interval in halves until
the resulting interval is extremely small
The root is then approximately equal to any value in the final
(very small) interval.
14

15. The Bisection Method (cont.)
• Example:
• Suppose the interval [a..b] is as follows:
15

16. The Bisection Method (cont.)
• We cut the interval [a..b] in the middle: m = (a+b)/2
16

17. The Bisection Method (cont.)
• Because sign of f(m) ≠ sign of f(a) , we proceed with the
search in the new interval [a..b]:
17

18. The Bisection Method (cont.)
We can use this statement to change to the new interval:
b = m;
18

19. 19
Basis of Bisection Method
Theorem
x
f(x)
xu
x
An equation f(x)=0, where f(x) is a real continuous function,
has at least one root between xl and xu if f(xl) f(xu) < 0.
Figure 1 At least one root exists between the two points if the function is
real, continuous, and changes sign.

20. x
f(x)
xu
x
20
Basis of Bisection Method
Figure 2 If function does not change sign between two
points, roots of the equation may still exist between the two
points.
 xf
  0xf

21. 21
Algorithm for Bisection Method

22. 22
Step 1
Choose x and xu as two guesses for the root such that
f(x) f(xu) < 0, or in other words, f(x) changes sign
between x and xu. This was demonstrated in Figure 1.
x
f(x)
xu
x
Figure 1

23. x
f(x)
xu
x
xm
23
Step 2
Estimate the root, xm of the equation f (x) = 0 as the mid
point between x and xu as
x
x
m =
xu 
2
Figure 5 Estimate of xm

24. 24
Step 3
Now check the following
a) If , then the root lies between x and
xm; then x = x ; xu = xm.
b) If , then the root lies between xm and
xu; then x = xm; xu = xu.
c) If ; then the root is xm. Stop the
algorithm if this is true.
    0ml xfxf
    0ml xfxf
    0ml xfxf

25. 25
Step 4
x
x
m =
xu 
2
100

 new
m
old
m
new
a
x
xxm
rootofestimatecurrentnew
mx
rootofestimatepreviousold
mx
Find the new estimate of the root
Find the absolute relative approximate error
where

26. 26
Step 5
Is ?
Yes
No
Go to Step 2 using new
upper and lower
guesses.
Stop the algorithm
Compare the absolute relative approximate error with
the pre-specified error tolerance .
a
s
sa 
Note one should also check whether the number of
iterations is more than the maximum number of iterations
allowed. If so, one needs to terminate the algorithm and
notify the user about it.

27. 27
Example 1
The floating ball has a specific gravity of 0.6 and has a
radius of 5.5 cm. You are asked to find the depth to
which the ball is submerged when floating in water.
Figure 6 Diagram of the floating ball

28. 28
Example 1 Cont.
The equation that gives the depth x to which the ball is
submerged under water is given by
a) Use the bisection method of finding roots of equations to
find the depth x to which the ball is submerged under
water. Conduct three iterations to estimate the root of
the above equation.
b) Find the absolute relative approximate error at the end
of each iteration, and the number of significant digits at
least correct at the end of each iteration.
010993.3165.0 423
 
xx

29. 29
Example 1 Cont.
From the physics of the problem, the ball would be
submerged between x = 0 and x = 2R,
where R = radius of the ball,
that is
 
11.00
055.020
20



x
x
Rx
Figure 6 Diagram of the floating ball

30. To aid in the understanding
of how this method works to
find the root of an equation,
the graph of f(x) is shown to
the right,
where
30
Example 1 Cont.
  423
1099331650 -
.x.xxf 
Figure 7 Graph of the function f(x)
Solution

31. 31
Example 1 Cont.
Let us assume
11.0
00.0


ux
x
Check if the function changes sign between x and xu .
       
        4423
4423
10662.210993.311.0165.011.011.0
10993.310993.30165.000




fxf
fxf
u
l
Hence
           010662.210993.311.00 44
 
ffxfxf ul
So there is at least on root between x and xu, that is between 0 and 0.11

32. 32
Example 1 Cont.
Figure 8 Graph demonstrating sign change between initial limits

33. 33
Example 1 Cont.
055.0
2
11.00
2




 u
m
xx
x 
       
           010655.610993.3055.00
10655.610993.3055.0165.0055.0055.0
54
5423




ffxfxf
fxf
ml
m
Iteration 1
The estimate of the root is
Hence the root is bracketed between xm and xu, that is, between 0.055
and 0.11. So, the lower and upper limits of the new bracket are
At this point, the absolute relative approximate error cannot be
calculated as we do not have a previous approximation.
11.0,055.0  ul xx
a

34. 34
Example 1 Cont.
Figure 9 Estimate of the root for Iteration 1

35. 35
Example 1 Cont.
0825.0
2
11.0055.0
2




 u
m
xx
x 
       
         010655.610622.1)0825.0(055.0
10622.110993.30825.0165.00825.00825.0
54
4423




ffxfxf
fxf
ml
m
Iteration 2
The estimate of the root is
Hence the root is bracketed between x and xm, that is, between 0.055
and 0.0825. So, the lower and upper limits of the new bracket are
0825.0,055.0  ul xx

36. 36
Example 1 Cont.
Figure 10 Estimate of the root for Iteration 2

37. 37
Example 1 Cont.
The absolute relative approximate error at the end of Iteration 2 isa
%333.33
100
0825.0
055.00825.0
100






 new
m
old
m
new
m
a
x
xx
None of the significant digits are at least correct in the estimate root of
xm = 0.0825 because the absolute relative approximate error is greater
than 5%.

38. 38
Example 1 Cont.
06875.0
2
0825.0055.0
2




 u
m
xx
x 
       
           010563.510655.606875.0055.0
10563.510993.306875.0165.006875.006875.0
55
5423




ffxfxf
fxf
ml
m
Iteration 3
The estimate of the root is
Hence the root is bracketed between x and xm, that is, between 0.055
and 0.06875. So, the lower and upper limits of the new bracket are
06875.0,055.0  ul xx

39. 39
Example 1 Cont.
Figure 11 Estimate of the root for Iteration 3

40. 40
Example 1 Cont.
The absolute relative approximate error at the end of Iteration 3 isa
%20
100
06875.0
0825.006875.0
100






 new
m
old
m
new
m
a
x
xx
Still none of the significant digits are at least correct in the estimated
root of the equation as the absolute relative approximate error is
greater than 5%.
Seven more iterations were conducted and these iterations are shown in
Table 1.

41. 41
Table 1 Cont.
Table 1 Root of f(x)=0 as function of number of iterations for
bisection method.
Iteration x xu xm a % f(xm)
1
2
3
4
5
6
7
8
9
10
0.00000
0.055
0.055
0.055
0.06188
0.06188
0.06188
0.06188
0.0623
0.0623
0.11
0.11
0.0825
0.06875
0.06875
0.06531
0.06359
0.06273
0.06273
0.06252
0.055
0.0825
0.06875
0.06188
0.06531
0.06359
0.06273
0.0623
0.06252
0.06241
----------
33.33
20.00
11.11
5.263
2.702
1.370
0.6897
0.3436
0.1721
6.655×10−5
−1.622×10−4
−5.563×10−5
4.484×10−6
−2.593×10−5
−1.0804×10−5
−3.176×10−6
6.497×10−7
−1.265×10−6
−3.0768×10−7

42. 42
Table 1 Cont.
Hence the number of significant digits at least correct is given by the
largest value or m for which
 
  463.23442.0log2
23442.0log
103442.0
105.01721.0
105.0
2
2
2








m
m
m
m
m
a
2m
So
The number of significant digits at least correct in the estimated root
of 0.06241 at the end of the 10th iteration is 2.

43. 43
Advantages
 Always convergent
 The root bracket gets halved with each
iteration - guaranteed.

44. 44
Drawbacks
 Slow convergence
 If one of the initial guesses is close to
the root, the convergence is slower

45. 45
Drawbacks (continued)
 If a function f(x) is such that it just
touches the x-axis it will be unable to find
the lower and upper guesses.
f(x)
x
  2
xxf 

46. 46
Drawbacks (continued)
 Function changes sign but root does not
exist
f(x)
x
 
x
xf
1
