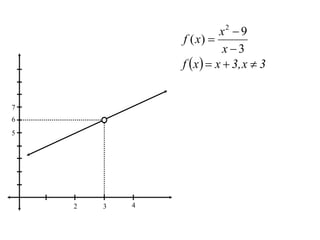
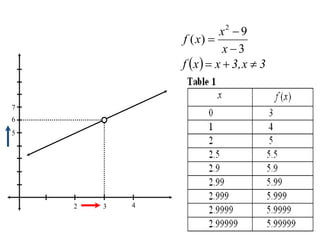
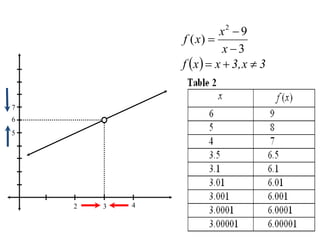
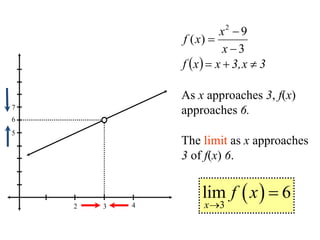
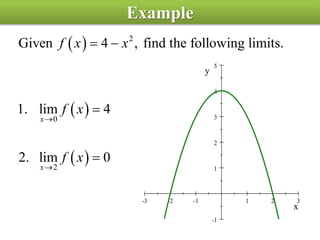
The document defines the limit of a function and how to determine if the limit exists at a given point. It provides an intuitive definition, then a more precise epsilon-delta definition. Examples are worked through to show how to use the definition to prove limits, including finding appropriate delta values given an epsilon and showing a function satisfies the definition.

1. Chapter 2
Limits and Continuity

2. 2.1 Limit of a Function

3.   3x,3xxf 
2
9
( )
3
x
f x
x



32 4
6
5
7

4.   3x,3xxf 
6
3
2
9
( )
3
x
f x
x



2 4
5
7

5.   3x,3xxf 
6
3
2
9
( )
3
x
f x
x



2 4
5
7

6.   3x,3xxf 
6
3
2
9
( )
3
x
f x
x



 3
lim 6
x
f x


The limit as x approaches
3 of f(x) 6.
2 4
5
7
As x approaches 3, f(x)
approaches 6.

7. Limit of a Function (an intuitive definition)
Let f be a function defined on some open interval
containing a except possibly at a itself. Then, the
limit of f as x approaches a is L, written as
 lim
x a
f x L


if f(x) gets closer and closer to one and only one
number L as x takes the values that are closer to a.

8. Limit of a Function (an intuitive definition)
To say that means that: lim
x a
f x L


The distance (or difference, to be more specific)
between f(x) and L can be made arbitrarily small
by requiring that x be sufficiently close to but
different from a.
Remark: The small distances (or differences)
stated above must be quantified to have a more
precise definition of limit.

9. Limit of a Function
Let and be positive real numbers,
i.e. 0 and 0. 
 
 
Think and as small positive numbers. 
“the distance between f(x) and L can be made
arbitrarily small”:
 f x L     f x L    
 L f x L    

10. Limit of a Function
Let and be positive real numbers,
i.e. 0 and 0. 
 
 
Think and as small positive numbers. 
“x be sufficiently close to but different from a”:
0 x a    wherea x a x a     

11. Limit of a Function
 
Let be a function defined on some open interval
containing , except possibly at .
The of the function as approaches is ,
written as lim ,
if for every
lim
0, there exists a 0,
it
x a
f
a a
x a L
f x L
 


 
 
such that
if 0 , then .x a f x L     

12. Example
 
 
 
2
0
2
Given 4 , find the following limits.
1. lim 4
2. lim 0
x
x
f x x
f x
f x


 


-3 -2 -1 1 2 3
-1
1
2
3
4
5
x
y

13. Proving Limits of a Function
 
 
To prove that lim .
i. Verify that is defined on some open interval
containing , except possibly at .
ii. Consider a positive epsilon ( 0).
iii. Find an expression for such that
whene
x a
f x L
f
a a
f x L






 
 
ver 0 .
iv. Show that if 0 then .
v. Form a conclusion.
x a
x a f x L

 
  
    

14. Example
 
 
 
 
3
Prove using the definition that lim 2 1 5.
Preliminary Analysis.
We want such that if then .
2 1 5 2 3
2 6 3
2
2 3 Choose .
2
x
x
x a f x L
x x
x x
x
  
 



 

 
   
    
   
  

15.  
Proof.
i. Since the function is a polynomial function,
it is defined on any open interval containing 3.
ii. Let 0.
iii. Choose .
2
iv. If 0 3 , then 3
2
2 3
2 6
2 1 5
x x
x
x
x










    
 
 
  
 3
v. Therefore, lim 2 1 5.
x
x

 

16. Example
 
 
   
 
 
 
1
Prove using the definition that lim 4 3 7.
Preliminary Analysis.
We want such that if then .
4 3 7 3 1
3 3 1
3
3 1 Choose .
3
3 1
x
x
x a f x L
x x
x x
x
x
  
 



 


 
   
     
     
   
   

17.  
Proof.
i. Since the function is a polynomial function,
it is defined on any open interval containing 1.
ii. Let 0.
iii. Choose .
3
iv. If 0 1 , then 1
3
3 1
3 1
3 3
x x
x
x
x











     
 
  
  
 
 1
3 3
4 3 7 .
v. Therefore, lim 4 3 7.
x
x
x
x



  
  
 

18. Challenge!
 Given 0, prove that lim .
x a
m mx b ma b

   