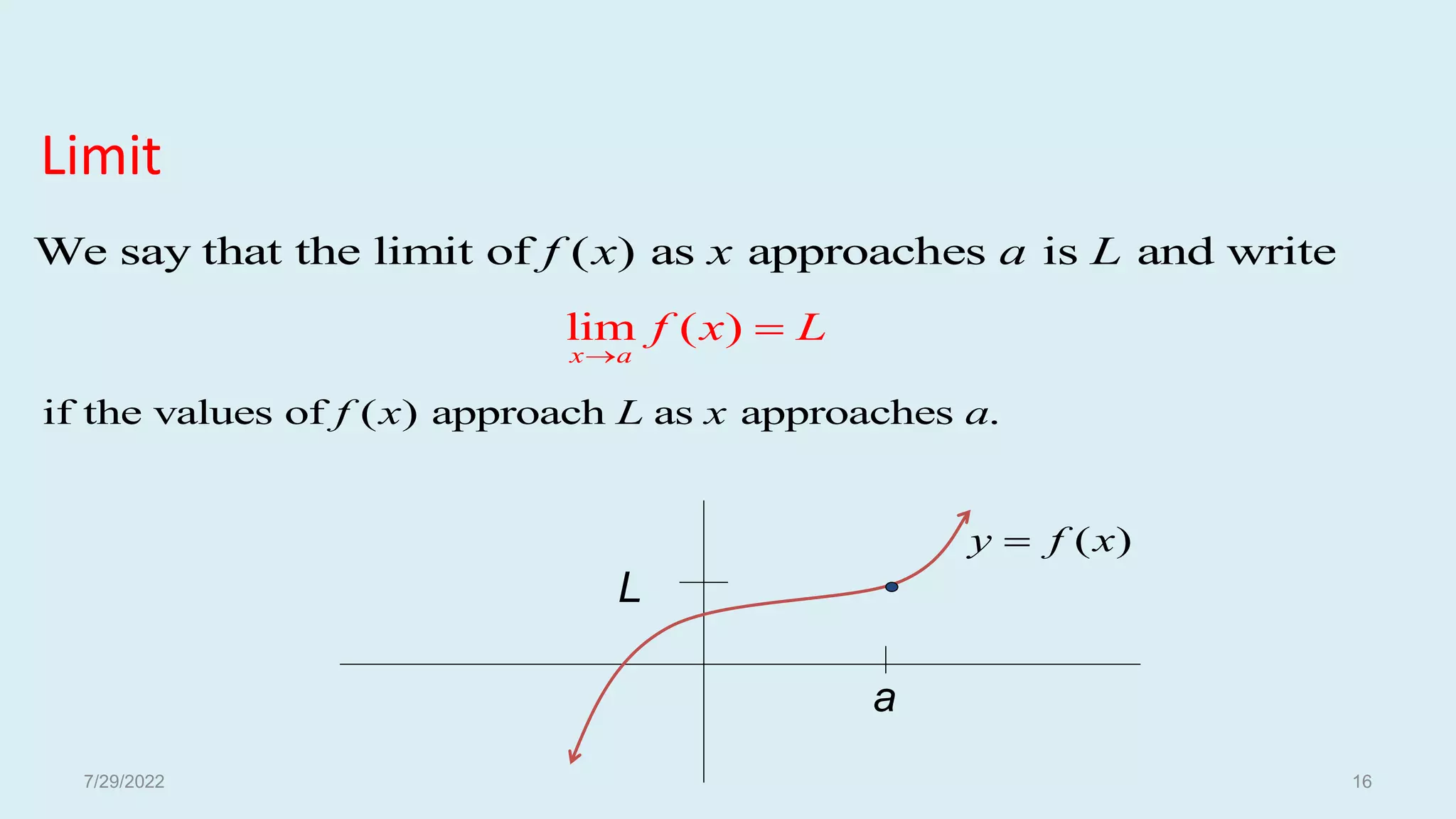
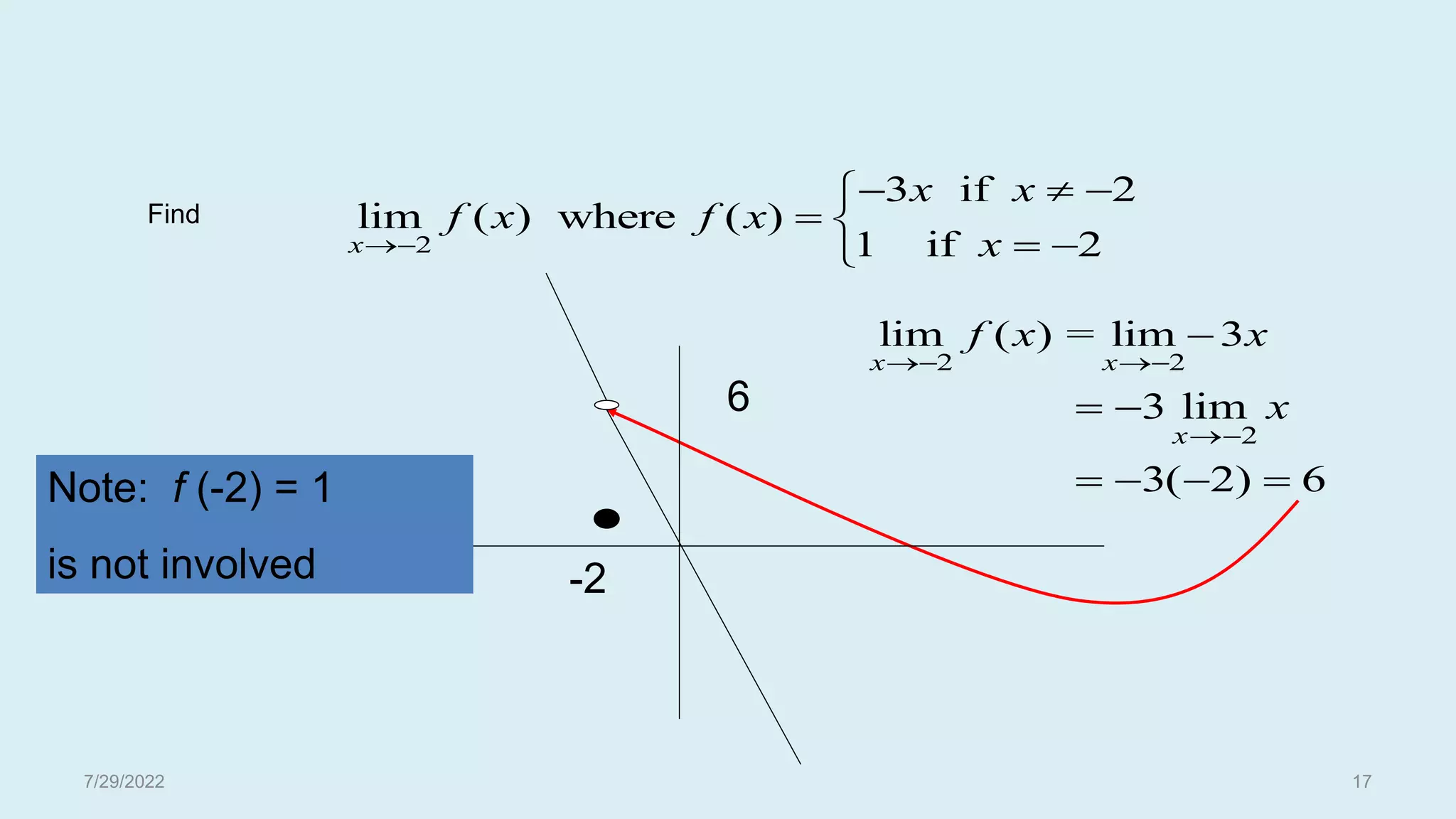
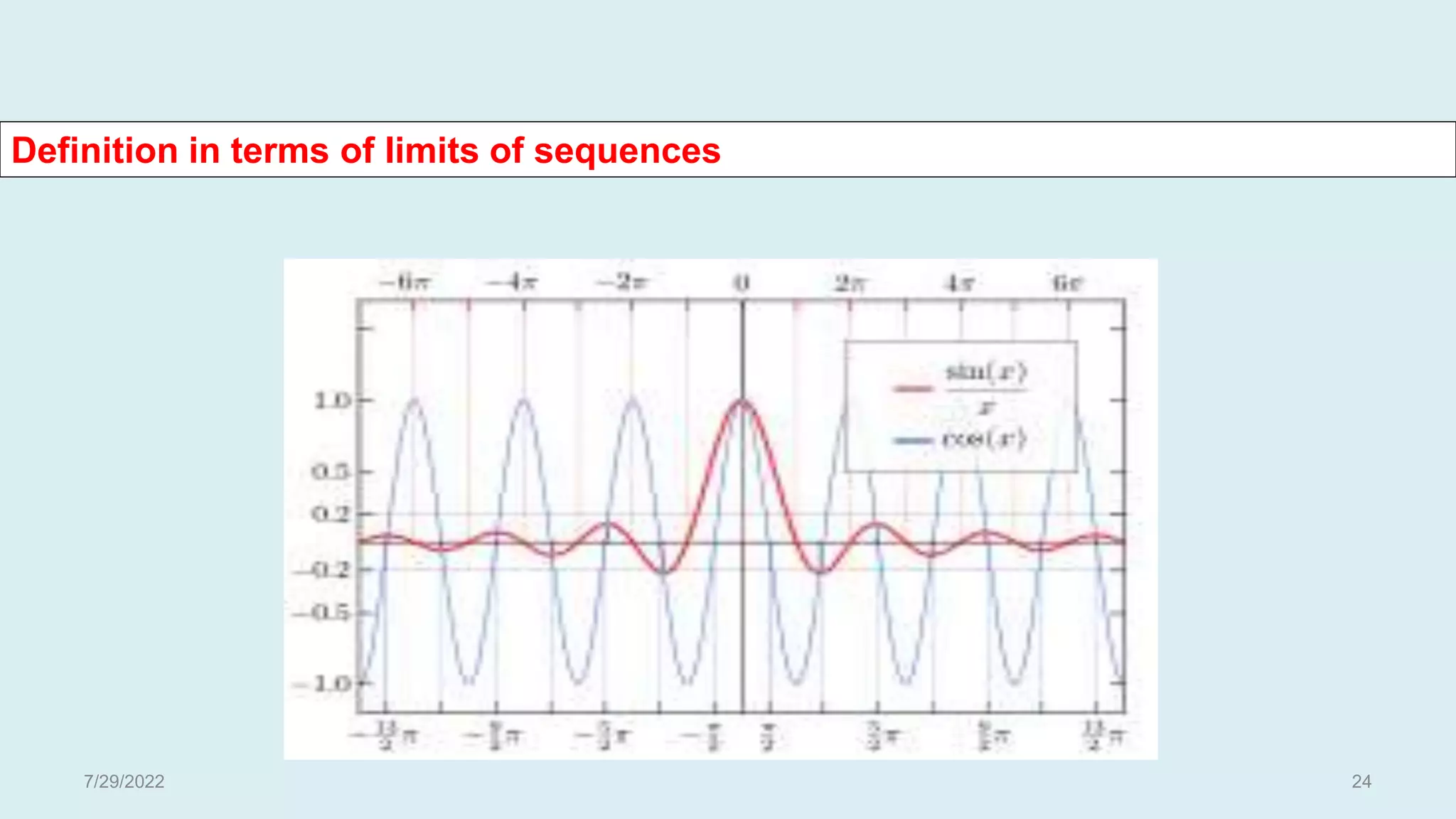
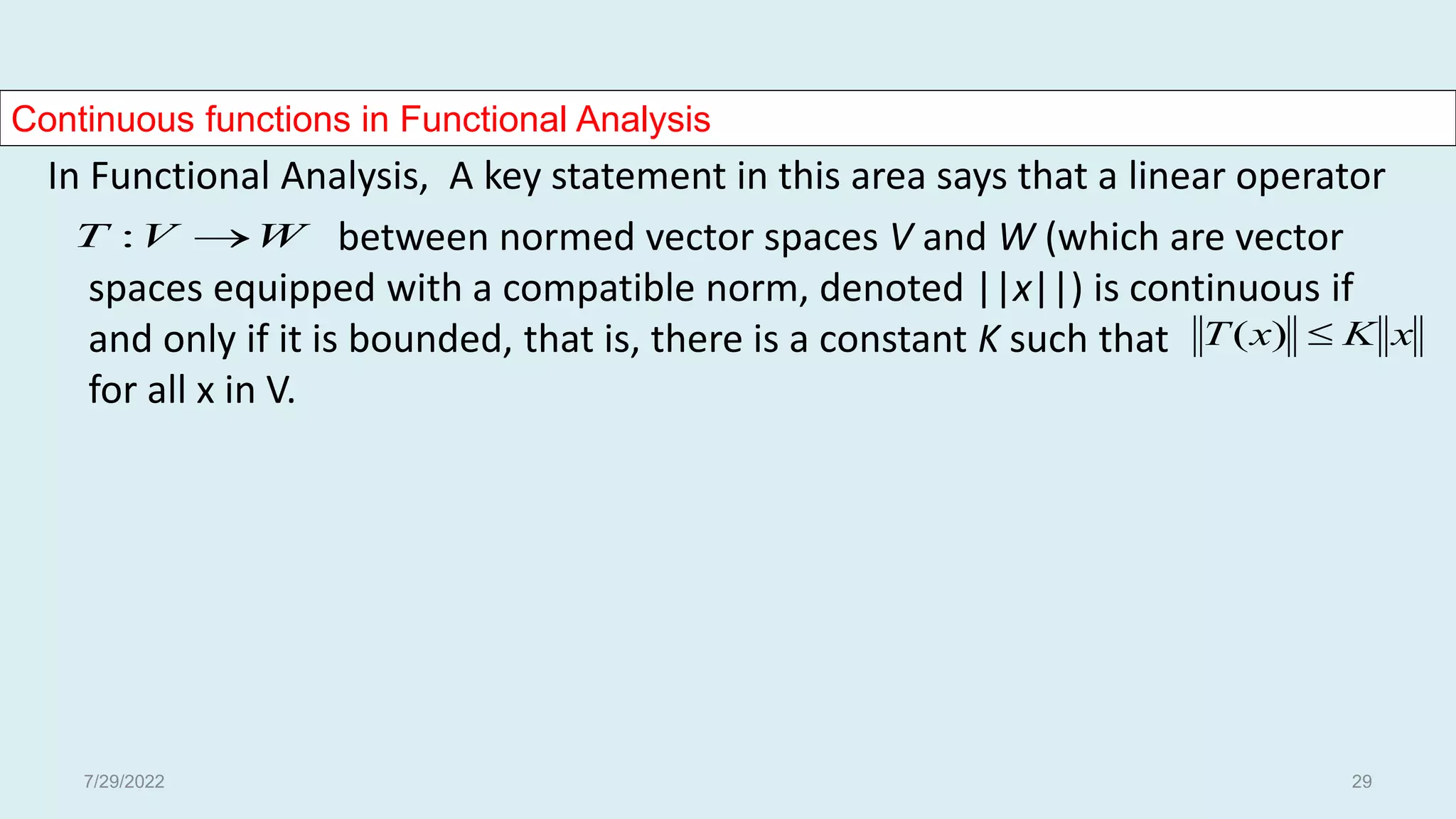
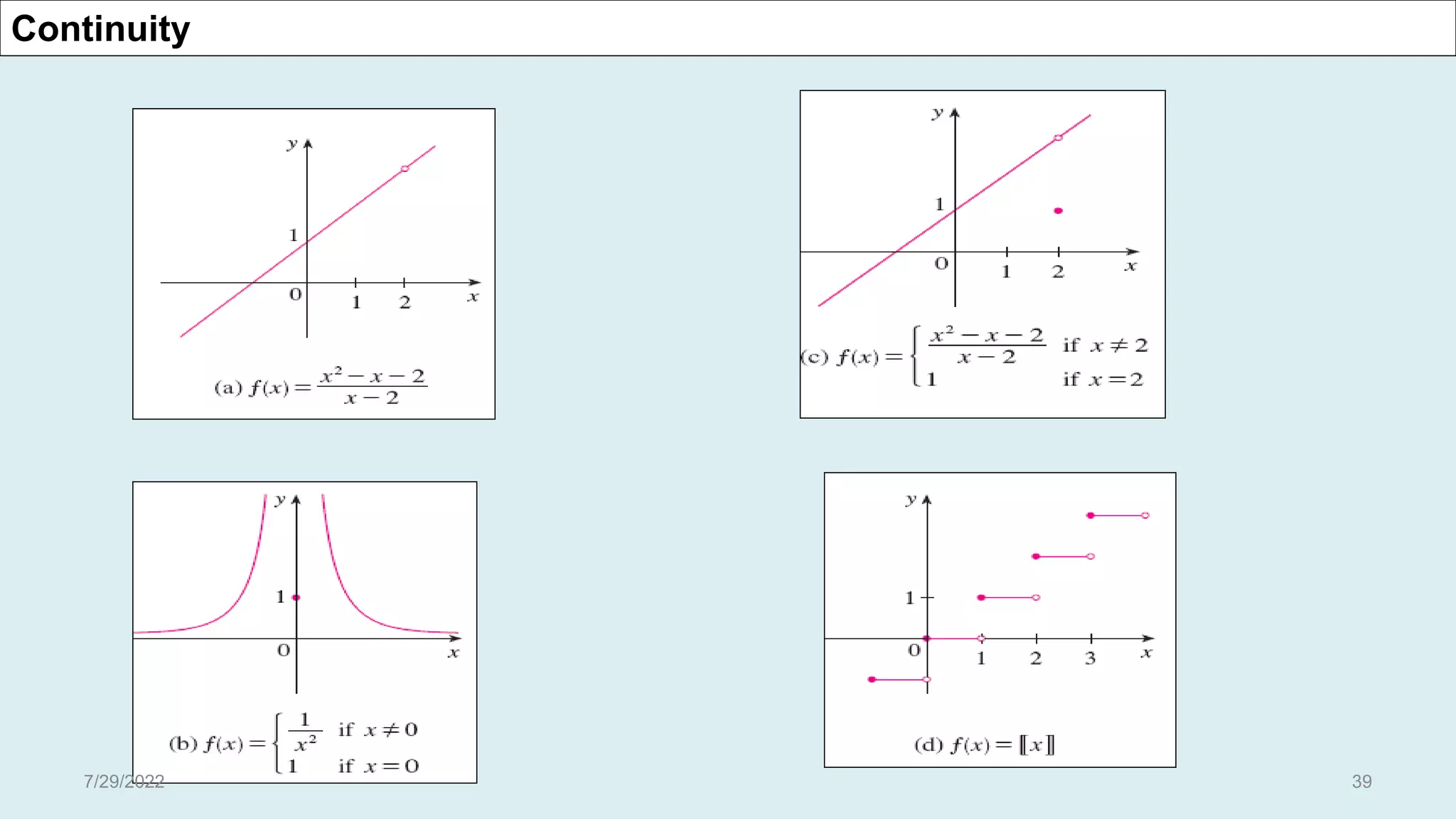
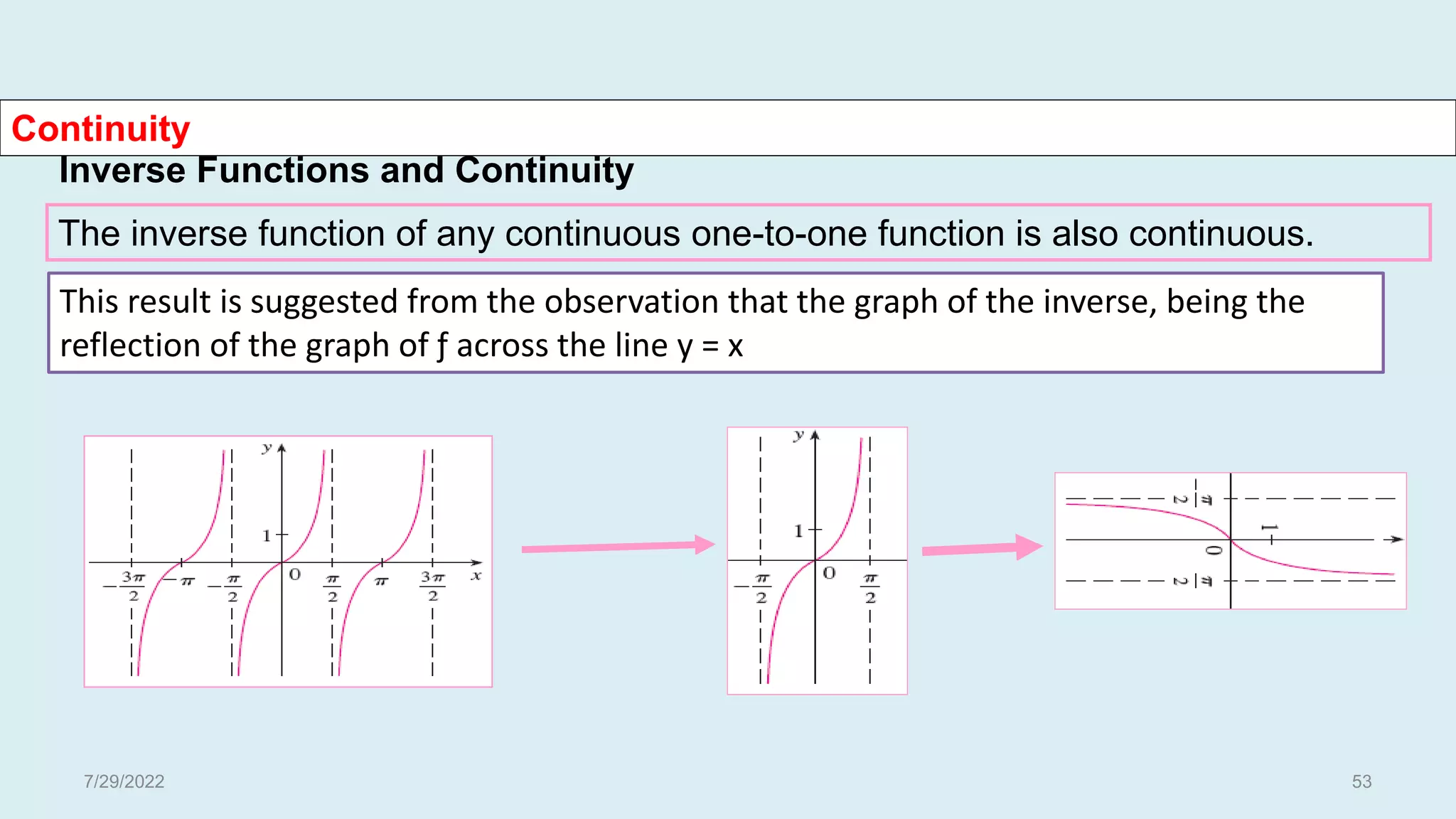
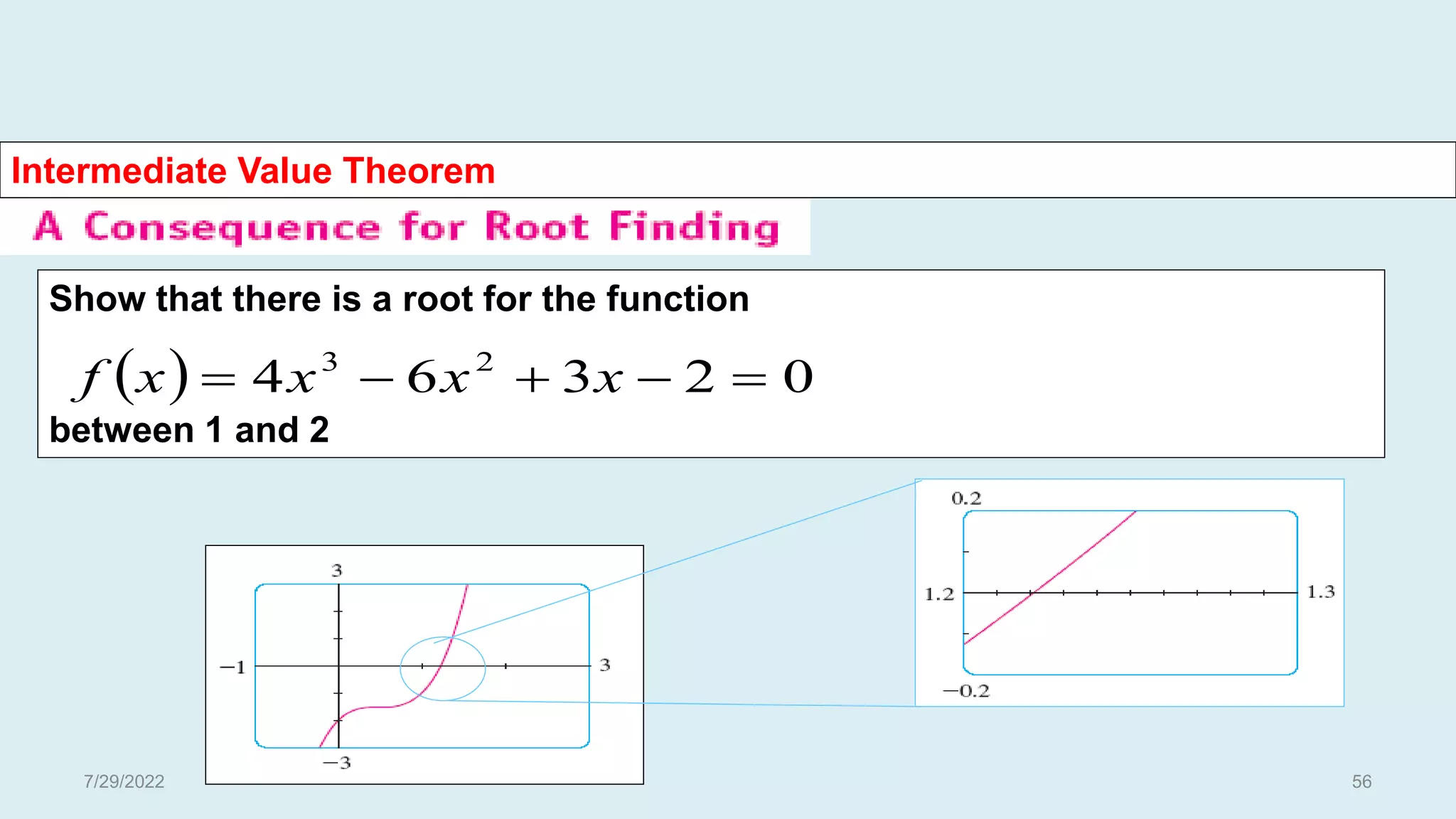
The document discusses basic concepts related to continuous functions. It begins with an introduction and motivation for studying continuous functions. Some key reasons mentioned are that continuous functions are needed for integration and as underlying functions in differential equations. The document then provides definitions of limits and continuity in terms of limits. It gives examples of determining limits and continuity for various functions. Contributors to the field like Bolzano, Cauchy, and Weierstrass are also acknowledged. The document concludes with additional definitions of continuity, examples, and discussions of uniform continuity.



































![Geometrically, IVT says that any horizontal line between ƒ(a) and ƒ(b) will cross the curve
at least once over the interval [a, b].
Intermediate Value Theorem
7/29/2022 54](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-54-2048.jpg)
![2) y0 between ƒ(a) and ƒ(b)
1) ƒ(x) continuous on [a,b]
y0=ƒ(c) for some c in [a,b]
The Intermediate Value Theorem
Intermediate Value Theorem
7/29/2022 55](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-55-2048.jpg)

![Let
Use Intermediate Value theorem to prove that f(x)=g(x) has a solution between 1 and 2
Intermediate Value Theorem
Solution:
is continuous on the interval [1,2]. And h(1) = -1, h(2) = 12.
Since h(1) = -1< 0 < h(2) = 12, there is a number c in
(1,2) such that h(c)=0. Therefore by IVT, there is root for
the h(x) = f(x) –g(x) = 0 or f(x)=g(x)
7
3
2
)
(
5
4
5 2
3
2
3
x
x
x
x
g
and
x
x
x
f
2
3
6
4
)
7
3
2
(
)
5
4
5
(
)
(
)
(
)
(
2
3
2
3
2
3
x
x
x
x
x
x
x
x
x
g
x
f
x
h
Let
7/29/2022 58](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-58-2048.jpg)







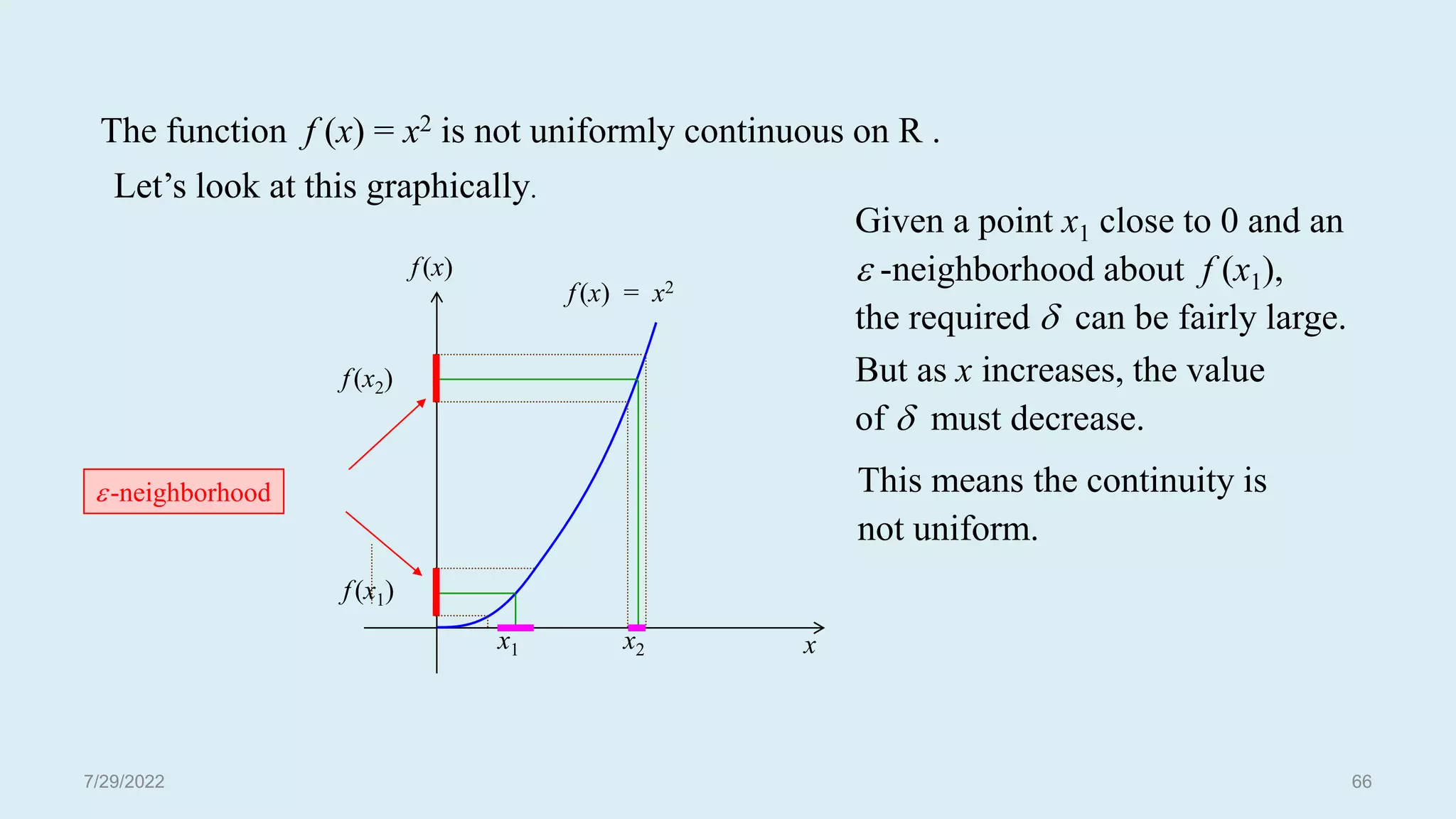
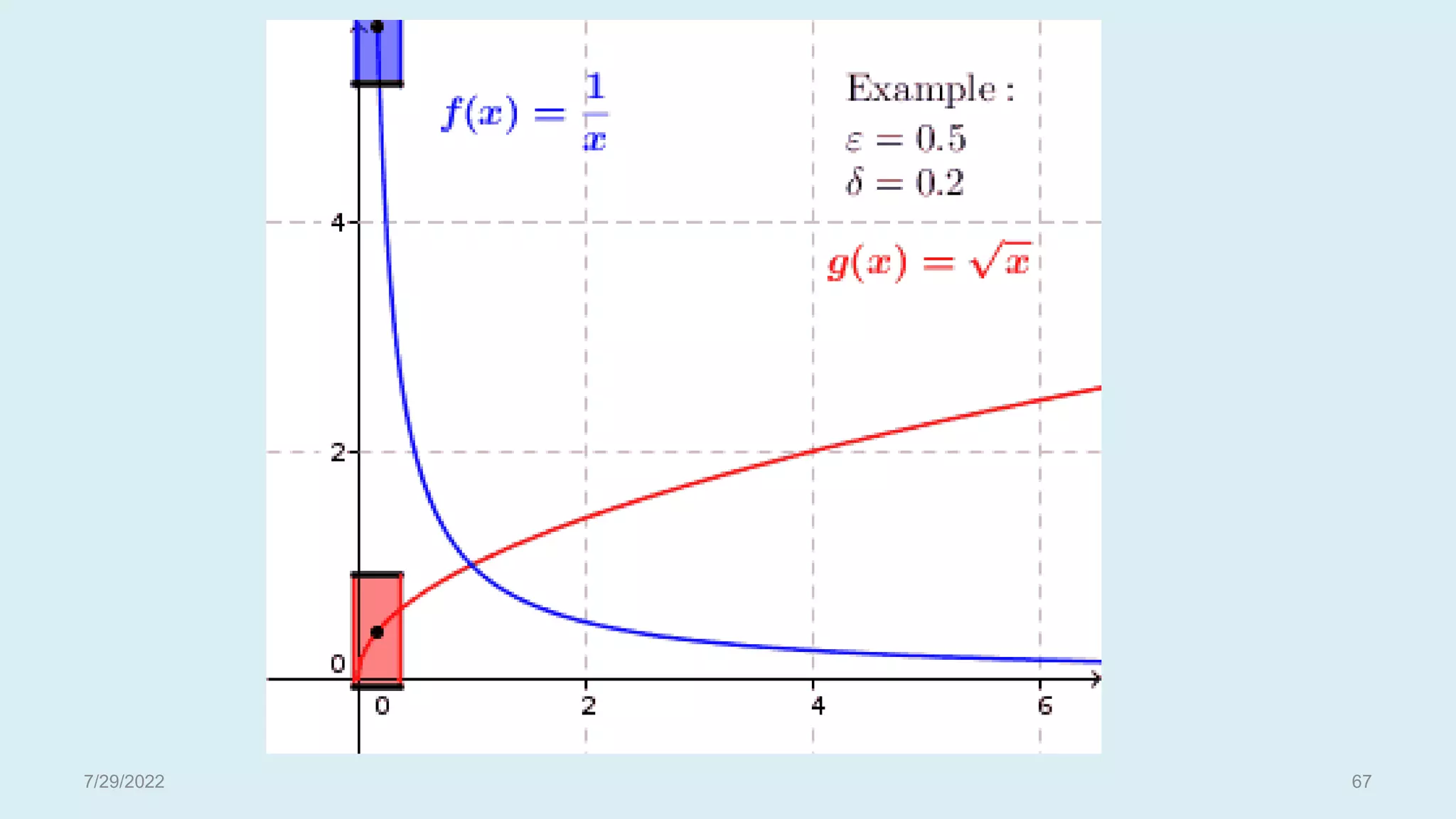






![The function f (x) = x2 is uniformly continuous on D if D is a bounded set.
For example, let D = [– 3, 3]. Then | x + y | 6.
So given 0, if = /6 and | x – y | < , we have
| f (x) – f ( y)| = | x2 – y2| = | x + y | | x – y |
6| x – y | < 6 = .
This is a special case of the following theorem.
Example Contd.
7/29/2022 75](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-75-2048.jpg)
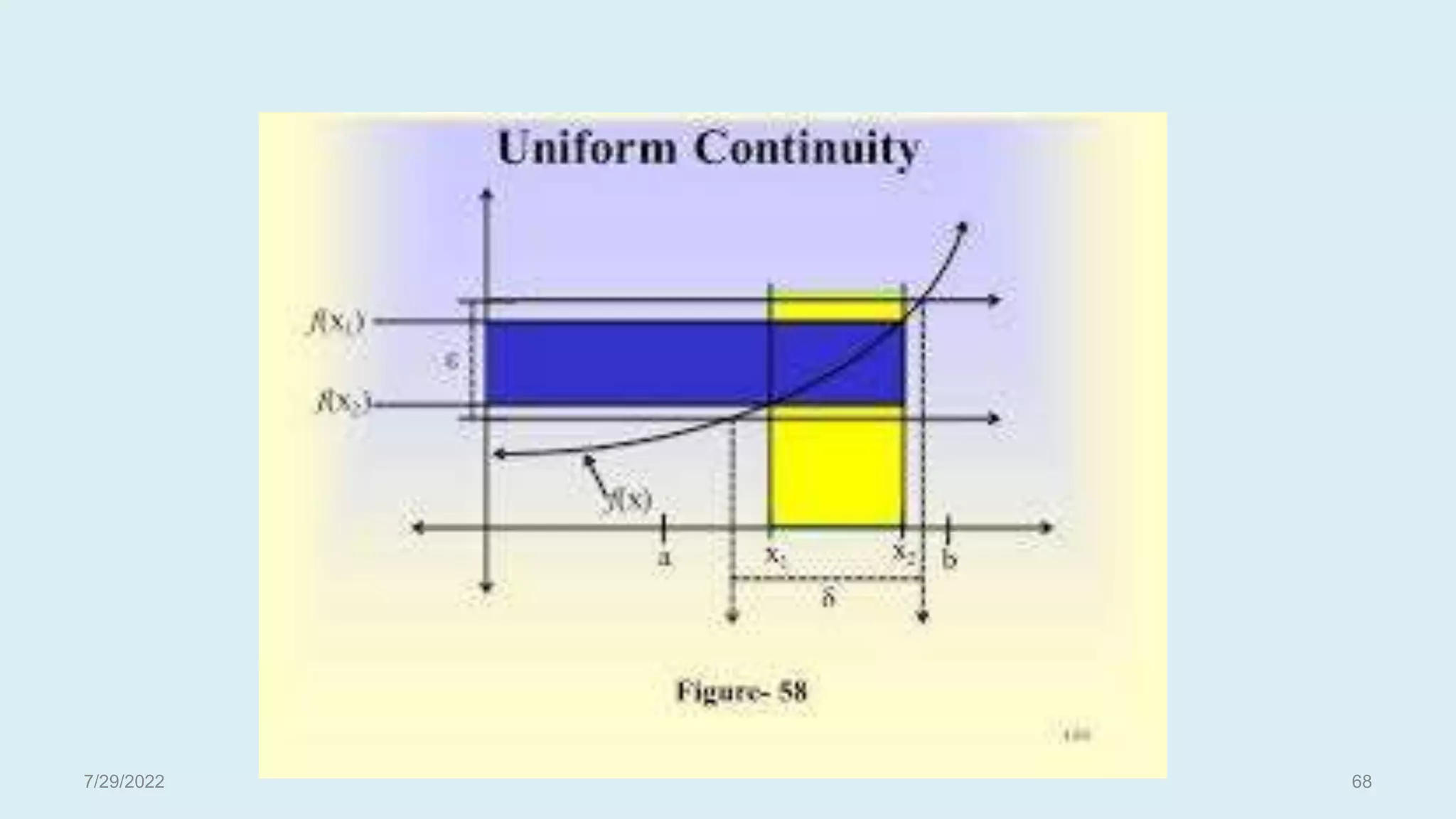
![If a function is continuous on a closed interval [a,b], then is Uniformly Continuous on
[a,b].
Proof:
Given that is continuous on [a,b].
To show that f is uniformly continuous on [a,b]
If possible suppose that is not uniformly continuous on [a,b]
That is such that whenever and
Thus for each , in [a,b] such that |f(xn)-f(yn)| whenever |xn-yn|<δn
By Bolazano-Weirstrass theorem, a convergent subsequence of <xn> converging to x0(say)
Theorem
y
x
f
]
,
[
, b
a
y
x
f
f
f
0
,
0
)
(
)
( y
f
x
f
N
n n
n y
x ,
7/29/2022 76](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-76-2048.jpg)
![If a function is continuous on a closed interval [a,b], then is Uniformly Continuous on
[a,b].
Proof:
Given that is continuous on [a,b].
To show that f is uniformly continuous on [a,b]
If possible suppose that is not uniformly continuous on [a,b]
That is such that whenever and
Thus for each , in [a,b] such that |f(xn)-f(yn)| whenever |xn-yn|<δn
By Bolazano-Weirstrass theorem, a convergent subsequence of <xn> converging to x0(say)
Theorem
y
x
f
]
,
[
, b
a
y
x
f
f
f
0
,
0
)
(
)
( y
f
x
f
N
n n
n y
x ,
7/29/2022 77](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-77-2048.jpg)
![0
x
x k
n
k
Lt
]
,
[
0 b
a
x
0
n
f
x
f k
n
k
Lt
0
n
f
y
f k
n
k
Lt
0
k
k n
n
k
y
f
x
f
Lt
k
k n
n y
f
x
f
f
as f is a continuous function at x0,<f(xnk)> converges to f(n0) and <f(ynk)> converges to f(n0).
Therefore
This is a contradiction. So our supposition is wrong
is Uniformly continuous on [a,b]
i.e.
Also and also 0
x
ynk
k
Lt
Also
7/29/2022 78](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-78-2048.jpg)

![Proof:
If f can be extended to a function that is continuous on the compact set [a, b],
then is uniformly continuous on [a, b].
Using the above theorem, we can derive a useful test to determine if a function is
uniformly continuous on a bounded open interval.
We say that a function an extension of if D E and
~
Theorem
A function f : (a, b) R is uniformly continuous on (a, b) iff it can be extended to a
function that is continuous on [a, b].
It follows that (and hence f ) is also uniformly continuous on the subset (a, b).
)
(
)
( f
dom
x
x
f
x
f
R
E
f
: R
D
f
:
f
f
f
f
7/29/2022 80](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-80-2048.jpg)

![REFERENCES
[1] Elementary Analysis by Kenneth A Ross.
[2] Mathematical Analysis, 2nd Edition by S.C. Malik and Savita Arora.
[3] Introduction to Real Analysis by Robert G. Bartle, Donald R. Sherbert.
[4] https://en.wikipedia.org/wiki/Continuous_function
[5] https://matheducators.stackexchange.com
[6] https://math.libretexts.org/Courses/Mount_Royal_University
[7] https://www.google.com/search?q=images
[8] Continuity in Software, Dick Hamlet, Portland State University
82
7/29/2022](https://image.slidesharecdn.com/continutiyoffunctions-220729070735-03d0ff29/75/Continutiy-of-Functions-ppt-82-2048.jpg)

