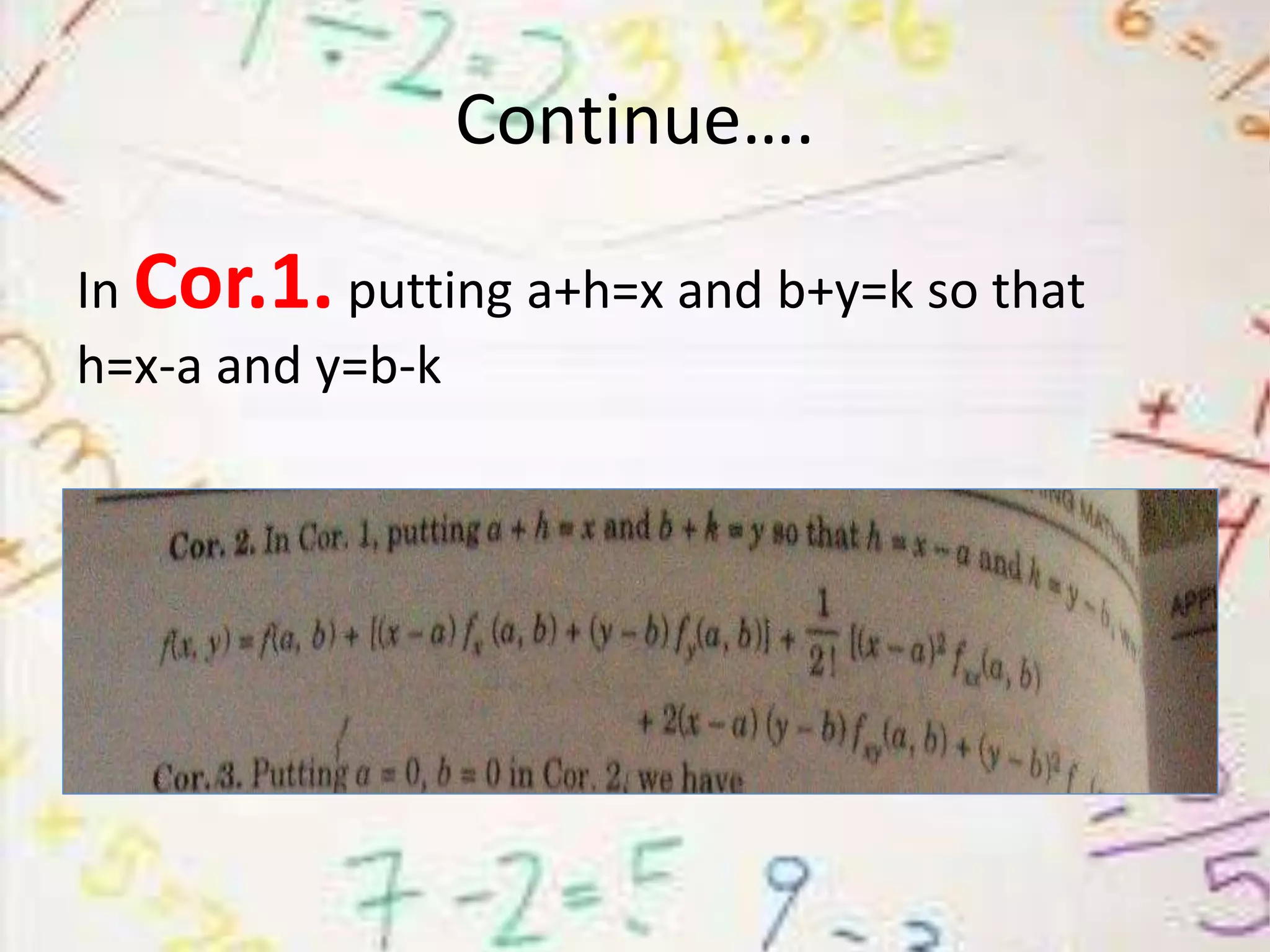This document discusses topics in partial differentiation including: 1) The geometrical meaning of partial derivatives as the slope of the tangent line to a surface. 2) Finding the equation of the tangent plane and normal line to a surface. 3) Taylor's theorem and Maclaurin's theorem for functions with two variables, which can be used to approximate functions and calculate errors.

1. Presentation on
Application of Partial
Differentiation

2. Geometrical Meaning of Partial
Derivative
The figure shows a plane y=b
intersects the surface z=f(x, y)
in the curve APCB. then
(¶z/¶x)y denotes the tangent
of the angle which the
tangent to the curve in which
plane y=b meets the surface
z=f(x,y) makes with the +ve
direction of the x-axis.

3. TANGENT
The equation of the
tangent plane
to the surface
F(x,y,z)=0 is

4. NORMAL
Equation of the normal at (x1,y1,z1) is

5. Example of tangent and normal
Find the equation of the tangent plane and
normal line to the surface xyz=a3 at (x1,y1,z1)

6. Taylor’s theorem for a function of two
variables
Taylor’s theorem for a function of a single
variable x, we have

7. Continue……
Cor.1. putting x=a and y=b in Taylor's
theorem, we have

8. Continue….
In Cor.1. putting a+h=x and b+y=k so that
h=x-a and y=b-k

9. Maclaurin’s theorem
In Cor.2. put a=0,b=0,we have

10. Example…

11. Errors and Approximations

12. Errors and Approximations

13. Example
What error in the common logarithm of a
number will be produced by an error of 1% in
the number.?

14. Maximum and Minimum
values

15. Maximum and Minimum
values

16. Local Maximum Value

17. Local minimum value

18. Maximum and minimum values

19. Working rule to find the extreme
values of a function z=f(x,y)

21. Lagrange’s method of undetermined
Multipliers
•

26. Advantages of Lagrange’s method
1. The stationary values of f(x,y,z) can be
determined directly even without
determining x,y,z explicitly
2. This method can be extended to a function of
several variables and subject to any number
of constraints.

27. Disadvantages of LaGrange's method
1. This method does not enable us to find
whether stationary point in maximum and
minimum. Further investigations are needed.
2. The only necessary condition but not
sufficient condition is