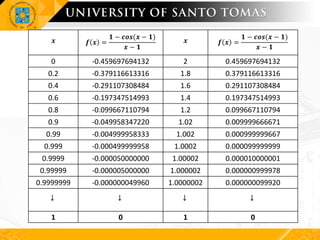
The document discusses the concept of limits in functions, including one-sided limits and various theorems associated with them. It provides definitions, examples, and techniques for evaluating limits, particularly in cases of indeterminate forms, along with practical exercises. Examples illustrate direct substitution, factoring, and the importance of one-sided limits to determine function behavior at specific points.

1. 1.1 The Limit
Of a Function,
One-sided limits
And theorems on limits
Prepared by:
Asst. Prof. Enrico M. Yambao, M.Sc.

2. The Limit of a Function
What is a limit and how does it differ from a value of the function
at the given number?
To answer this question and to illustrate the concept of limit,
consider the function defined by
𝑓 𝑥 =
1−cos(𝑥−1)
𝑥−1
Observe that this function 𝑓 is not even defined at 1, that is, 𝑓(1)
is undefined (Why?).
But, can we say something about the value of 𝑓(𝑥) when 𝑥 is
made closer and closer to 1?

3. 𝒙 𝒇 𝒙 =
𝟏 − 𝒄𝒐𝒔(𝒙 − 𝟏)
𝒙 − 𝟏
𝒙 𝒇 𝒙 =
𝟏 − 𝒄𝒐𝒔(𝒙 − 𝟏)
𝒙 − 𝟏
0 -0.459697694132 2 0.459697694132
0.2 -0.379116613316 1.8 0.379116613316
0.4 -0.291107308484 1.6 0.291107308484
0.6 -0.197347514993 1.4 0.197347514993
0.8 -0.099667110794 1.2 0.099667110794
0.9 -0.049958347220 1.02 0.009999666671
0.99 -0.004999958333 1.002 0.000999999667
0.999 -0.000499999958 1.0002 0.000099999999
0.9999 -0.000050000000 1.00002 0.000010000001
0.99999 -0.000005000000 1.000002 0.000000999978
0.9999999 -0.000000049960 1.0000002 0.000000099920
↓ ↓ ↓ ↓
1 0 1 0

4. Based on the generated values of 𝑓 in the table, when 𝑥 gets closer and
closer to 1, be it through values smaller than 1 or through values greater
than 1, 𝑓(𝑥) becomes closer and closer to 0. That is, if 𝑥 is made close
enough to 1, then 𝑓 𝑥 will become sufficiently close to 0. In symbols, this
behavior of 𝑓(𝑥) as 𝑥 approaches 1 is indicated by writing lim
𝑥→1
𝑓(𝑥) = 0.
Thus, this definition of a limit:
Definition: Let 𝑓(𝑥) be a function that is defined at every number in an
interval that contains the number 𝑎, except possibly at 𝑎 itself. The real
number 𝑳 is said to be the limit of 𝒇 at 𝒂 if 𝑓 𝑥 can be made sufficiently
close to 𝐿, whenever one wishes, by making 𝑥 close enough to 𝑎 and we
write
𝐥𝐢𝐦
𝒙→𝒂
𝒇(𝒙) = 𝑳
which is read “ the limit of 𝑓 𝑥 as 𝑥 approaches 𝑎 is equal to 𝐿”.

5. One-Sided Limits
The notation 𝐥𝐢𝐦
𝒙→𝒂
𝒇(𝒙) denoting the limit of a function, if it exists, refers
to the two-sided limit of the function 𝑓 since 𝑥 can approach 𝑎 in two
possible directions : from the right, i.e, through values greater than 𝑎,
and from the left, i.e., through values greater than 𝑎, and from the left.
To indicate that 𝑥 is just approaching 𝑎 from the right, we write
𝐥𝐢𝐦
𝒙→𝒂+
𝒇(𝒙)
and to indicate that 𝑥 is just approaching 𝑎 from the left, we write
𝐥𝐢𝐦
𝒙→𝒂−
𝒇(𝒙)

6. Theorems on Limits
Theorem: Assume that lim
𝑥→𝑎
𝑓(𝑥) and lim
𝑥→𝑎
𝑔(𝑥) both exist.
1. The limit of a function, if it exists, is always unique.
2. The limit of a function at the number 𝑎 exists ,if and only if,
the one-sided limits at 𝑎 both exist and are equal. That is,
lim
𝑥→𝑎
𝑓(𝑥) = 𝐿 if and only if, lim
𝑥→𝑎+
𝑓(𝑥) = lim
𝑥→𝑎−
𝑓(𝑥) = 𝐿
3 . lim
𝑥→𝑎
𝑐 = 𝑐, 𝑐 is a constant
4. lim
𝑥→𝑎
𝑥 = 𝑎
5. lim
𝑥→𝑎
𝑐 ⋅ 𝑓 𝑥 = 𝑐 lim 𝑓 𝑥
𝑥→𝑎
for any constant 𝑐

7. Theorems on Limits
6. lim
𝑥→𝑎
𝑓(𝑥) ± 𝑔(𝑥) = lim 𝑓 𝑥
𝑥→𝑎
± lim
𝑥→𝑎
𝑔 𝑥
7. lim
𝑥→𝑎
𝑓(𝑥) ⋅ 𝑔(𝑥) = lim
x→a
𝑓 𝑥 ⋅ lim 𝑔 𝑥
𝑥→𝑎
8. lim
𝑥→𝑎
𝑓(𝑥)
𝑔(𝑥)
=
lim
𝑥→𝑎
𝑓(𝑥)
lim
𝑥→𝑎
𝑔(𝑥)
, provided lim
𝑥→𝑎
𝑔(𝑥) ≠ 0
9. lim
𝑥→𝑎
𝑓(𝑥) 𝑛 = lim
𝑥→𝑎
𝑓(𝑥)
𝑛
10. lim
𝑥→𝑎
𝑛
𝑓(𝑥) = 𝑛
lim
𝑥→𝑎
𝑓(𝑥) , for any 𝑛 ≥ 2

8. Evaluation of Limits
Example 1. Use the theorems on limits to evaluate lim
𝑥→2
𝑥2+3𝑥+6
2𝑥3−4
.
Solution: lim
𝑥→2
𝑥2+3𝑥+6
2𝑥3−4
=
lim 𝑥2+3𝑥+6
𝑥→2
lim
𝑥→2
2𝑥3−4
=
lim 𝑥2
𝑥→2
+3 lim x+
𝑥→2
lim
𝑥→2
6
2lim
𝑥→2
𝑥3−lim
𝑥→2
4
=
22+3 2 +6
2(2)3−4
=
16
12
=
4
12
Thus, lim
𝑥→2
𝑥2+3𝑥+6
2𝑥3−4
=
1
3
So, what have you noticed upon application of the theorems on limits?

9. • The evaluation is just reduced to calculating the value of the function
at 𝑥 = 2 , so that in general, lim
𝑥→𝑎
𝑓(𝑥) can be evaluated by direct
substitution of 𝑎 into 𝑓(𝑥).
• However, if direct substitution yields the indeterminate form
0
0
,
manipulate the expression that defines 𝑓(𝑥) to get rid of the factor
that makes the limit indeterminate.
• If 𝑓(𝑥) is a rational function, the manipulation is done simply by
factoring and simplifying 𝑓(𝑥) before substituting the number 𝑎. If
𝑓(𝑥) is not rational, a different kind of manipulation is necessary. For
example, rationalizing the denominator of 𝑓(𝑥) .
Example 2. Calculate lim
𝑥→−2
(5𝑥2 − 𝑥 + 3), if it exists.
Solution: As 𝑥 → −2,
5𝑥2 − 𝑥 + 3 → 5(−2)2 − (−2) + 3 = 20 + 2 + 3 = 25
Thus, lim
𝑥→−2
(5𝑥2 − 𝑥 + 3) = 25.

10. Example 3. Evaluate lim
x→7
2𝑥2−13𝑥−7
𝑥−7
, if it exists.
Solution: As 𝑥 → 7,
2𝑥2−13𝑥−7
𝑥−7
→
2(7)2−13(7)−7
7−7
=
0
0
(𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑡𝑒)
By factoring,
2𝑥2−13𝑥−7
𝑥−7
=
(2𝑥+1)(𝑥−7)
𝑥−7
= 2𝑥 + 1
Hence, lim
x→7
2𝑥2−13𝑥−7
𝑥−7
= lim
x→7
2𝑥 + 1 = 2 7 + 1 = 15

11. Example 5. Determine if lim
𝑥→3
𝑓(𝑥) exists given that
𝑓(𝑥) = ቊ2𝑥2
− 𝑥 if 𝑥 < 3
3 − 𝑥 if 𝑥 ≥ 3
.
Solution: Since 𝑓(𝑥) has different definitions in the vicinity of 𝑥 = 3, we
investigate the one-sided limits at 3 to determine if lim
𝑥→3
𝑓(𝑥) exists.
Now, as 𝑥 → 3−, 𝑥 < 3. Thus,
lim
𝑥→3−
𝑓(𝑥) = lim
𝑥→3−
(2𝑥2 − 𝑥) = 2(3)2 − 3 = 18 − 3 = 15
Similarly, as 𝑥 → 3+, 𝑥 > 3. Thus,
lim
𝑥→3+
𝑓(𝑥) = lim
𝑥→3+
(3 − 𝑥) = 3 − 3 = 0
Since lim
𝑥→3−
𝑓(𝑥) ≠ lim
𝑥→3+
𝑓(𝑥),
lim
𝑥→3
𝑓(𝑥) does not exist.

12. Example 4. Evaluate lim
𝑥→1
1−𝑥
1− 𝑥
, if it exists.
Solution: As 𝑥 → 1,
1−𝑥
1− 𝑥
→
1−1
1−1
=
0
0
(indeterminate).
Rationalize the denominator to yield
1−𝑥
1− 𝑥
⋅
1+ 𝑥
1+ 𝑥
=
1+ 𝑥−𝑥−𝑥 𝑥
1−𝑥
=
1+ 𝑥 −𝑥 1+ 𝑥
1−𝑥
=
1+ 𝑥 1−𝑥
1−𝑥
= 1 + 𝑥
Hence, lim
x→1
1−𝑥
1− 𝑥
= lim
𝑥→1
(1 + 𝑥) = 1 + 1 = 2.
Alternate Solution:
lim
𝑥→1
1−𝑥
1− 𝑥
= lim
𝑥→1
1− 𝑥
2
1− 𝑥
= lim
𝑥→1
1− 𝑥 1+ 𝑥
1− 𝑥
= lim
𝑥→1
1 + 𝑥
= 1 + 1
Thus, lim
𝑥→1
1−𝑥
1− 𝑥
= 2

13. Exercises: Use the theorems on limits to evaluate each of the following, if it exists.
1. lim
𝑥→−1
2𝑥3
− 4𝑥2
+ 5𝑥 − 10 7. lim
𝑥→5
𝑥2+1
2𝑥+2−2
2. lim
𝑥→3
9𝑥2−16
𝑥2−4
8. lim
𝑥→2
𝑥−2
𝑥+2
3. lim
𝑥→−1/2
4𝑥2+4𝑥+1
2𝑥2−𝑥−1
9. lim
𝑥→−3
𝑥3+27
𝑥2−9
4. lim
𝑥→2
𝑥−2
𝑥2−3𝑥+2
10. lim
𝑥→2
6−𝑥−𝑥
𝑥2−4
5. lim
𝑥→1
𝑥3+1
𝑥+1
11. lim
𝑥→2
𝑓(𝑥) if 𝑓 𝑥 = ቊ
2𝑥, 𝑥 ≤ 2
3𝑥 − 2, 𝑥 > 2
6. lim
𝑥→5
𝑥2+5− 30
𝑥−5
12. lim
𝑥→1
𝑓(𝑥) if 𝑓 𝑥 = ൝
𝑥2
+ 2, 𝑥 < 1
4𝑥 + 5, 𝑥 > 1