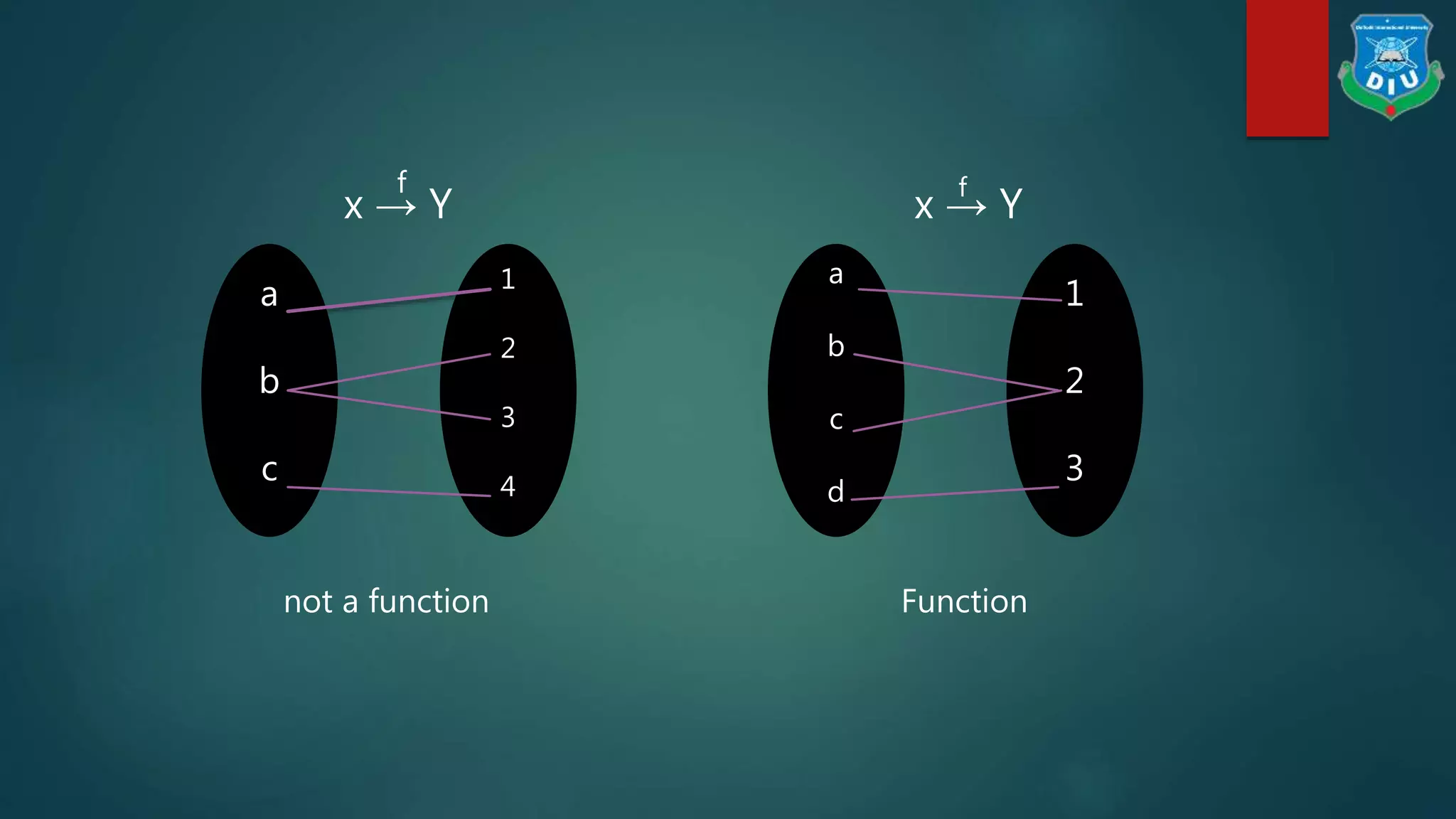
This document defines key concepts related to functions including domain, co-domain, and range. It provides examples of determining the domain and range of various functions. The domain of a function is the set of inputs, the co-domain is the set of all possible outputs, and the range is the set of actual outputs. Examples show how to use inequalities to find the domain by determining when a function gives real values and how to manipulate equations to find the range.

1. GOOD MORNING

2. Domain and Range for different Function

3. What is Function ?
 If f is a rule which associates every element of a set X with a unique
element of a set Y , then the rule f is called function from set X into set Y .
 Simply f : x→ y is a relation in which for each element in a set X , there is
a unique element of a set Y .

4. a
b
c
a
b
c
d
1
2
3
4
1
2
3
x → Y
f
x → Y
f
not a function Function

5. Function
 We can explain function in graph by using vertical line test . If we draw a straight
line on graph and if this straight line cut the graph only one point then this graph
represent a function , otherwise not .
 Example :- y = x2
x - 2 - 1 0 1 2
y 4 1 0 1 4
This is a function
X` X
Y
Y`

6. Again :
y = ±√x
y = √x
x 0 1 2 3
y 0 1 1.41 1.73
y = - √x
x 0 1 2 3
y 0 - 1 -1.41 -1.73
This is not function
X` X
Y
Y`

7. Parts of Function
 Domain
 Co - Domain
 Range

8. What is Domain ?
 If f : A – B is a function where A , B ≠ Φ then the set A is called the
domain of f .
 Domain of f is denoted by Df
 Example: when the function f(x) = x2 is given the values x = {1,2,3,...} then
{1,2,3,...} is the domain.

9. What is Co - Domain ?
 If f : A – B is a function where A , B ≠ Φ then the set B is called the co –
domain .
 Co – domain of f is denoted by codf
 Example :- If f : A → B is a function where A = { 0,1, 2 , 3 } and
B = { 2 , 5 , 8 ,11 , 15 } then the co – domain f is
codf = { 2 , 5 , 8 ,11 , 15 }

10. What is Range
 If f : A – B is a function where A , B ≠ Φ then the subset B which contains
all related elements of A is called the Range of f .
 Range of function is denoted by Rf
 If f : A → B is a function which is defined by f ( x ) = 3x + 2
 Here A = { 0 , 1 , 2 , 3 } and B = { 2 , 5 , 8 , 11 , 15 }
 If f ( x ) = 3x + 2 then f ( 0 ) = 2 , f ( 1 ) = 5 , f ( 2 ) = 8 , f ( 3 ) = 11
 Since range of f Rf = { 2 , 5 , 8 , 11 }

11.  Question :- If A = { - 3 , -1 , 0 , 1 , 3 } , all values are set of [R and function f : A → [R
is defined by f ( x ) = x2 + x + 1 . Find the domain and range of f .
 Solution: Given that , f ( x ) = x2 + x + 1
Here , f is defined by all values of set A
So, the domain of f Df = { - 3 , - 1 , o , 1 , 3 } ( Ans. )
And f ( - 3 ) = 7, f ( -1 ) = 1, f ( 0 ) = 1 , f ( 1 ) = 3 , f ( 3 ) = 13
So , the range f Rf = { 1 , 3 , 7 , 13 } ( Ans.)
Examples:

12. Examples:
Question : - Find domain and range of the function y = √ x2 – 7x + 12
Solution : - Given function is
y = √ x2 – 7x + 12
Here y gives real values if and only if , x2 – 7x + 12 ≥ 0
or , x2 – 4x – 3x +12 ≥ 0
or , x ( x – 4 ) – 3 ( x – 4 ) ≥ 0
or , ( x – 4 ) ( x – 3 ) ≥ 0
The inequality is satisfied if x ≤ 3 or x ≥ 4
So , the domain of the given function is Df = ( - ∞ , 3 ] U [ 4 , ∞ )

13. Again we have , y =√ x2 – 7x + 12 - - - - ( 1 )
The values of y in ( 1 ) are positive or zero i.e. y ≥ 0
Now , y2 = x2 – 7x + 12 [ squaring both sides ]
or , x2 – 7x + 12 - y2 = 0
In the above equation the values of x will be real if and only its Discriminant ≥ 0
i.e. 72 – 4 ( 12 – y2 ) ≥ 0 [ b2 – 4 ac ≥ 0 ]
or , 49 – 4 ( 12 – y2 ) ≥ 0
or , 49 – 48 + 4y2 ≥ 0
or , 1 + 4y2 ≥ 0
The above equation is possible for all real values of y but from ( 1 ) we have y ≥ 0
So , the range of the given function is Rf = [ 0 , ∞ )
( Ans. )

14. Examples:
Question :- Find the domain and range of the function :
y =
x – 3
2x + 1
Here y is undefined if 2x + 1 = 0
or , x = - 1
2
So , y gives real values for all real values of x except x = - 1
2
Therefore , the domain of the given function is ,
Df = [R – { -1
2
}

15. Again we have ,
y =
x – 3
2x + 1
or , 2xy + y = x – 3
or , 2xy – x + y + 3 = 0
or , y + 3 = x – 2xy
or , x ( 1 – 2y ) = y + 3
y + 3
1 – 2y
or , x =
Here x is undefined if 1 – 2y = 0
or , y =
1
2

16. So , x gives real values for all real values of y except y =
1
2
Therefore the range of the given function is
Rf = [R – { 1
2
}
( Ans. )

17. Examples:
Question : - Find the domain and range of the function y = √2x+5
Solution : - Given function is y = √2x+5
Here y gives real values if and only if 2x + 5 ≥ 0
or , x ≥ -
5
2
Therefore the domain of the given function is Df = [ - 5/2 , ∞ )

18. Again , y = √2x + 5 - - - - - ( 1 )
The values of y in ( 1 ) are positive or zero i . e . y ≥ 0
Now y2 = 2x + 5 ; y ≥ 0
or , 2x = y2 – 5 ; y ≥ 0
or , x =
y2 – 5
2
; y ≥ 0
Here x gives real values for all real values of y but in ( 1 ) we have y ≥ 0
So , the range of the given function is Rf = [ 0 , ∞ )
( Ans. )

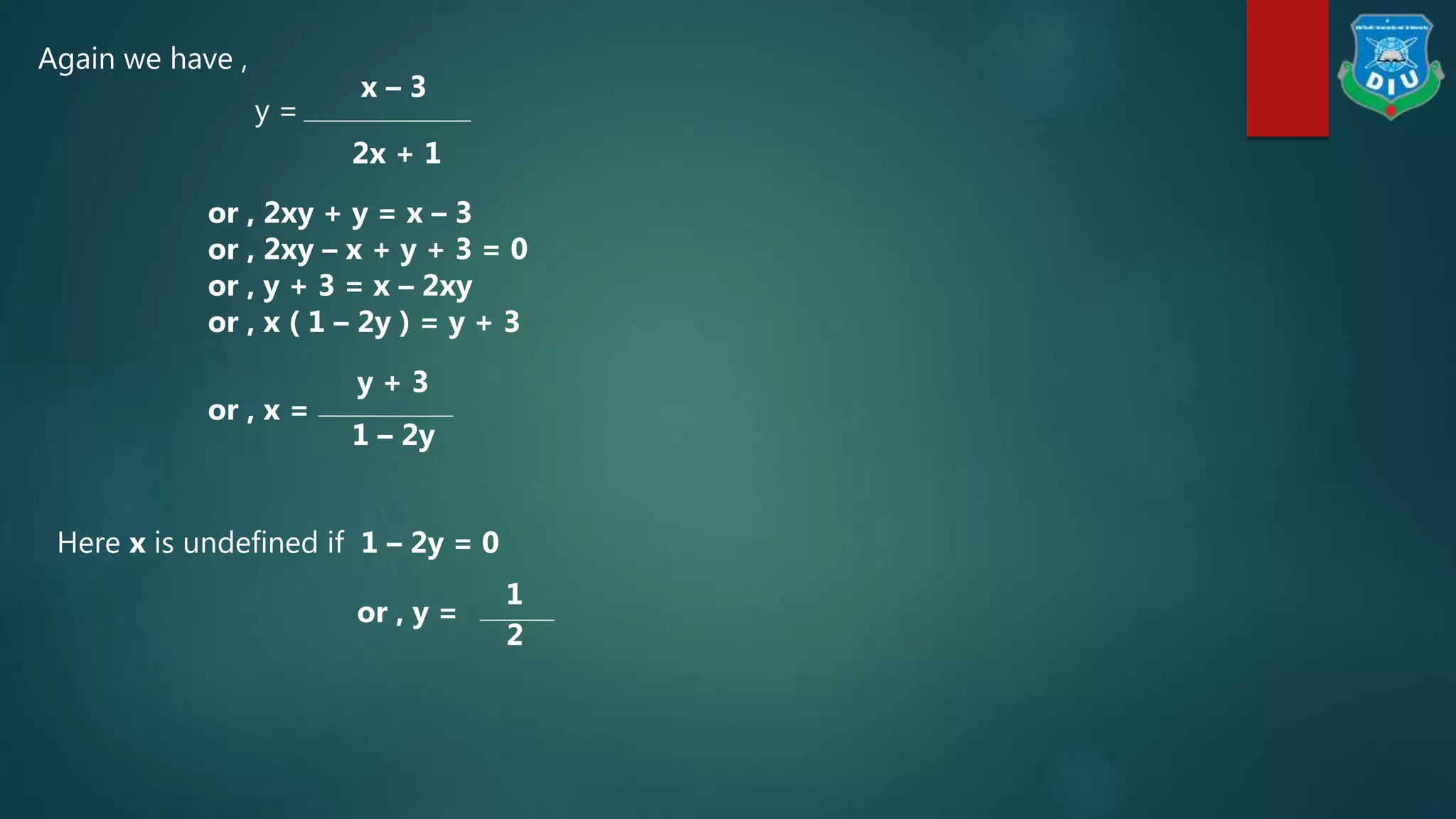
19. Examples:
Question:- Find the domain and range of the function : y = x2 + 3x + 2 .
Solution : Given function is y = x2 + 3x + 2
Here y gives real values for all real values of x
So, the domain of the given function is Df = [R
Again we have , y = x2 + 3x + 2
or , x2 + 3x + 2 – y = 0
In the above equation the values of x will be real if and only if its
Discriminant ≥ 0
i.e. 32 – 4.1 ( 2 – y ) ≥ 0 [ b2 – 4ac ≥ 0 ]
or, 9 – 4 ( 2 – y ) ≥ 0
or , 9 – 8 + 4y ≥ 0
or , 4y ≥ - 1
or , y ≥ -
1
4

20. Therefore , the range of the given function is
Rf = [ -
1
4
, ∞ )
( Ans. )

21. Have you any question ?

23. Created by
Md
Touhidul
Islam
Shawan
B.Sc. In CSE
Daffodil
International
University