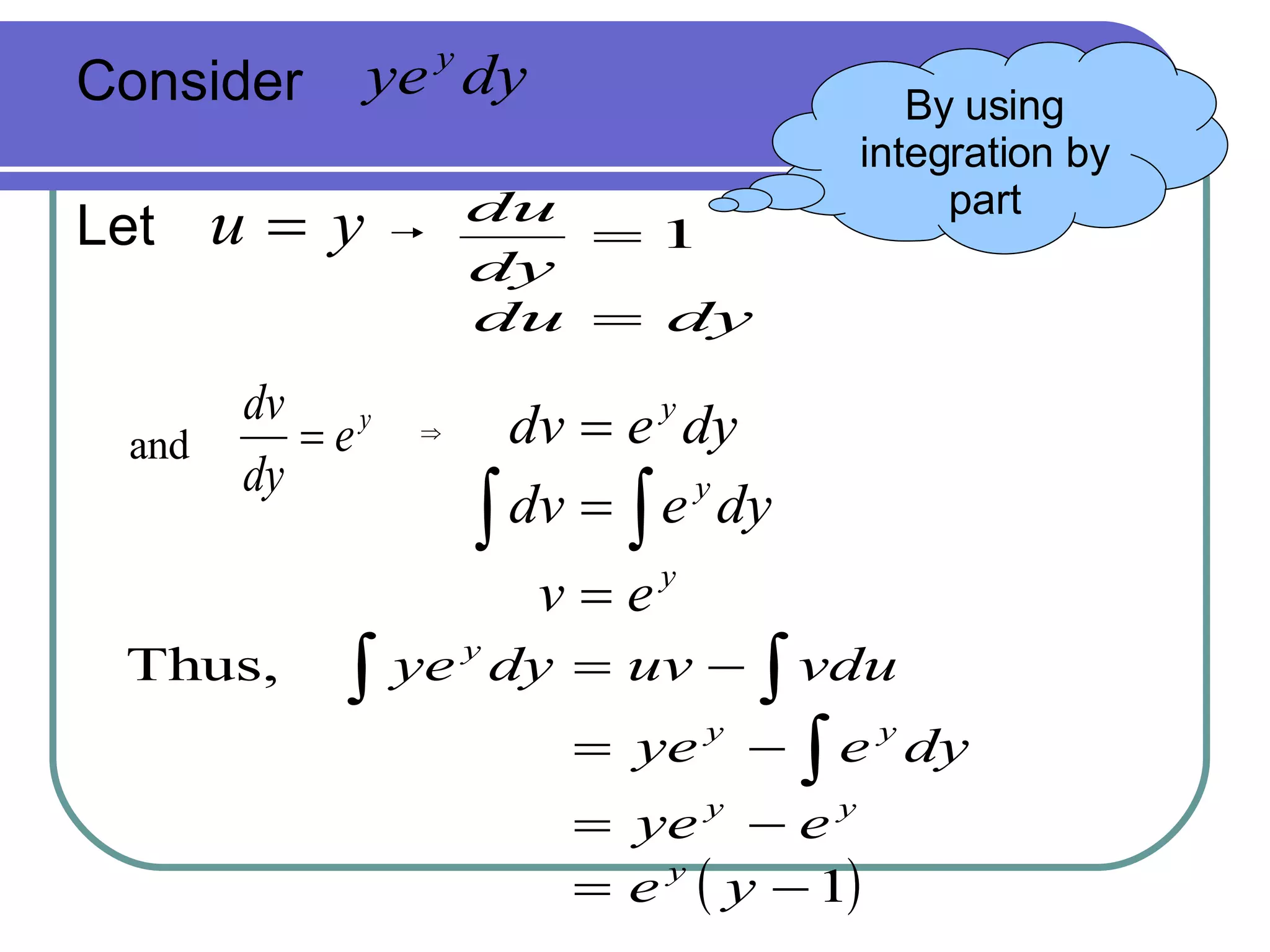
This document discusses differential equations and their solutions. It defines differential equations as equations involving derivatives. It notes that solutions can be general, containing an arbitrary constant, or particular, containing an initial value. Examples are given of separating variables and integrating to find the general solution to first order differential equations.

1. CHAPTER 2 Differential Equation

2. Introduction Consider x as an independent variable and y as dependent variable. An equation that involves at least one derivative of y with respect to x, e.g. Is known as a differential equation or common differential equation .

3. b) c) d) a) Example of Differential Equation

4. Order is the highest derivative Degree is the highest power of the highest derivative Examples: a) This DE has order 2 (the highest derivative appearing is the second derivative) and degree 1 (the power of the highest derivative is 1.) Order & Degree

5. In this chapter we only deal with first order, first degree differential equations. A solution for a differential equation is a function whose elements and derivatives may be substituted into the differential equation. There are two types of solution for differential equations

6. General solution – The general solution of a differential equation contains an arbitrary constant c . Particular solution - The particular solution of a differential equation contains a specified initial value and containing no constant. Solutions

7. Examples Of General Solution This is already in the required form, so we simply integrate: , c is constant

8. Example First we must separate the variables: Multiply throughout by dx Divide throughout by y Divide throughout by x

9. This gives us: We now integrate ,

10. Example First we must separate the variables: Multiply throughout by dx Divide throughout by Divide throughout by

11. This gives us: We now integrate:

12. Separable Variables and Integrating Factors Example Solve the differential equation First we must separate the variables: Consider :

13. By using substitution,

14. Consider Let and By using integration by part

15. The General Solution :

16. Example Solve the differential equation when x =0, y=5 First we must separate the variables: We now integrate:

17. We now use the information which means at , to find c . So the particular solution is: gives

18. Exercise : Solve the initial value problem. Express the solution implicitly. a. b.