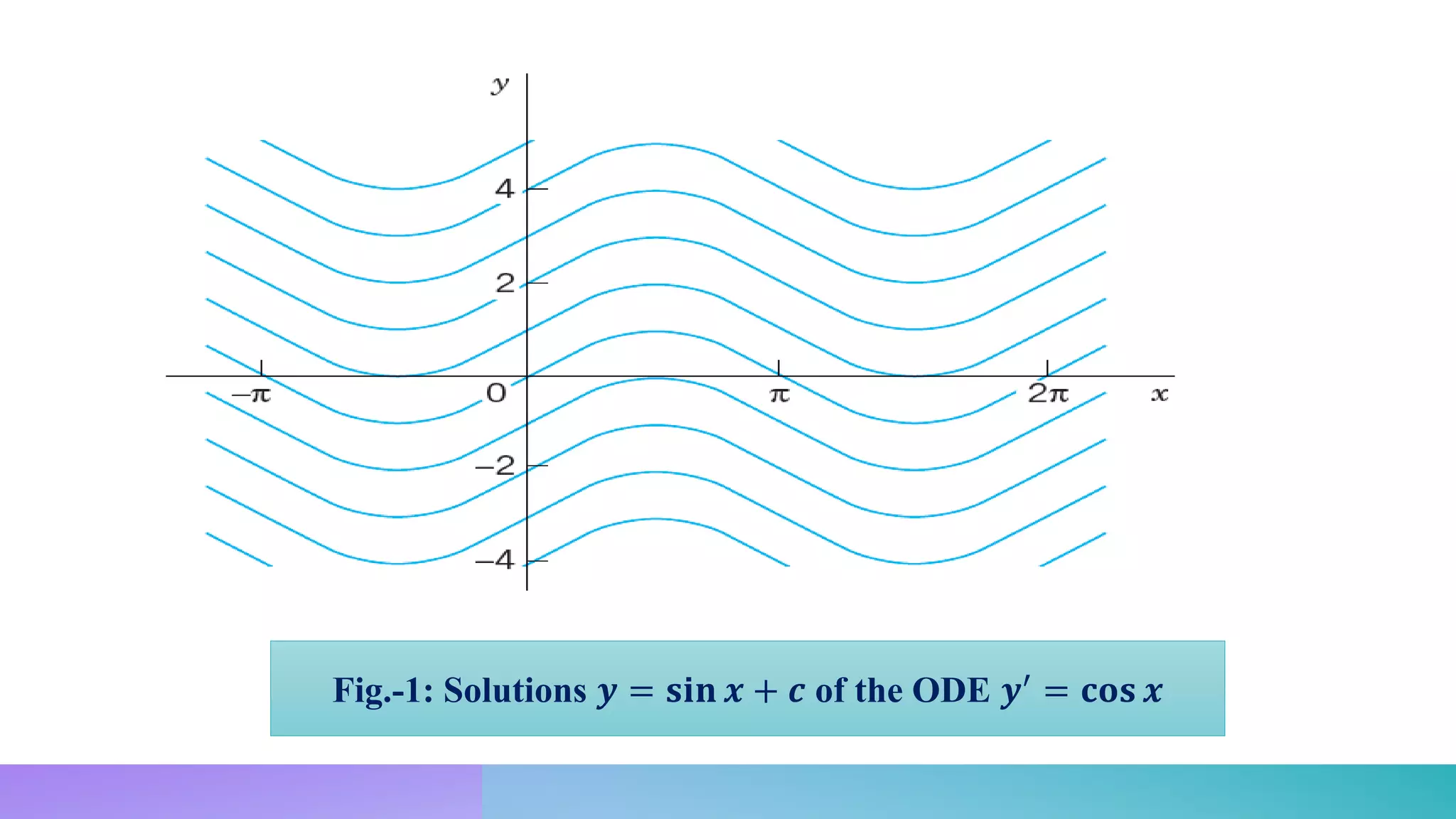
This document provides an overview of differential equations. It defines key terms like differential, derivative, and ordinary and partial differential equations. It explains that a differential equation is an equation involving differentials or derivatives. The document also discusses solutions to differential equations. Specifically, it notes that the general solution contains as many arbitrary constants as the order of the differential equation. Two examples are provided to illustrate this property.

1. D I F F E R E N T I A L
E Q U A T I O N S
M D . A M I N U L I S L A M
D E P T . O F
N A T U R A L S C I E N C E
P O R T C I T Y
I N T E R N A T I O N A L
U N I V E R S I T Y

2.  In mathematics, the history of differential equations traces the development of "differential equations" from
calculus, which itself was independently invented by English physicist IsaacNewton and German
mathematician Gottfried Leibniz.
 The history of the subject of differential equations, in concise form, from a synopsis of the recent
article “The History of Differential Equations, 1670- 1950”
“Differential equations began with Leibniz, the Bernoulli brothers, and others from the 1680s, not
long after Newton’s ‘fluxional equations’ in the 1670s.”
History

3. Differential: The expression of the form 𝑑𝑦 = 𝑓′ 𝑥 𝑑𝑥 is called the
differential of y or 𝑓 𝑥 .
Example: Let 𝑦 = 𝑓 𝑥 = 𝑥2. Then d𝑦 = 2𝑥 𝑑𝑥
Derivative: Let 𝑓 𝑥 be defined at any point 𝑥0 𝑖𝑛 𝑎, 𝑏 . The derivative of 𝑓 𝑥 at 𝑥0 is
defined as
𝑓′ 𝑥0 = lim
ℎ→0
𝑓 𝑥0 + ℎ − 𝑓(𝑥0)
ℎ
Provided the limit exists and finite

4. Definition:
An equation involving differentials or differential coefficients (derivative) is called a
differential equation.
Example
Differential Equations

5. ODE(Ordinary Differential Equations):
An equation contains only ordinary derivatives of one dependent variable of a single
independent variable. For Example
PDE(Partial Differential Equations):
An equation contains partial derivatives of one or more dependent variables of two or more
independentvariables. For Example,
Types of Differential Equations

6. A solution of a differential equation is any
relation between the variables involved which
satisfies the differential equation.
Such a relation, when substituted in the
differential equations, makes left and right hand
sides identically equal.
For example, 𝒚 = 𝒂𝒙 𝟐 + 𝒃𝒙 is a solution of
the following differential equation:
𝒅 𝟐
𝒚
𝒅𝒙 𝟐
−
𝟐
𝒙
𝒅𝒚
𝒅𝒙
+
𝟐𝒚
𝒙 𝟐
= 𝟎 … . (1)
Because on substitution of 𝑦 = 𝑎𝑥2 + 𝑏𝑥,
𝑑𝑦
𝑑𝑥
= 2𝑎𝑥 + 𝑏 𝑎𝑛𝑑
𝑑2 𝑦
𝑑𝑥2 = 2𝑎. 1 + 0 = 2𝑎
In the differential equation (1), we get
𝑳. 𝑯. 𝑺
= 2𝑎 −
2
𝑥
2𝑎𝑥 + 𝑏 +
2
𝑥2
(𝑎𝑥2 + 𝑏𝑥)
= 2𝑎 − 4𝑎 −
2𝑏
𝑥
+ 2𝑎 +
2𝑏
𝑥
= 0 = 𝑹. 𝑯. 𝑺
Solution of Differential Equations:

7. The solution of a differential equation in which the number of arbitrary constants is equal to
the order of the differential equation is called the general solution.
General or Complete Solution of a Differential Equation
Particular Solution of a Differential Equation
If particular values are given to the arbitrary constant in the general solution then the solution
so obtained is called the particular solution.
That is, a particular solution doesn’t contain any arbitrary constant.

8. Geometrically, the general solution of an ordinary differential equation is a family of infinitely
many solution curves.
Geometric Interpretation of Solution of Differential Equation
Solution by Calculus. Solution Curve
The ODE 𝒚′ = 𝐜𝐨𝐬 𝒙 can be solved directly by integration on both sides. Indeed, using
calculus, we obtain 𝒚 = 𝐬𝐢𝐧 𝒙 + 𝒄, where c is an arbitrary constant. This is a family of solutions.
Each value of c gives one of these curves.
Figure 1 shows some of them, 𝑐 = −4, −3, −2, −1, 0, 1, 2, 3, 4.

9. Fig.-1: Solutions 𝒚 = 𝐬𝐢𝐧 𝒙 + 𝒄 of the ODE 𝒚′
= 𝐜𝐨𝐬 𝒙

10. Example-1: Let 𝑦 = 𝐶𝑒 𝑥
… … (𝑖)
Then differentiating (i) on both sides w.r.t x, we get
𝑑𝑦
𝑑𝑥
= 𝐶𝑒 𝑥 = 𝑦
𝑜𝑟,
𝑑𝑦
𝑑𝑥
− 𝑦 = 0
Which is a differential equation of order 1.The number of arbitrary constants in (i) is 1
Therefore, number of arbitrary constants in the solution =the order of the differential
equation
The number of arbitrary constants in the solution is equal to the order of the differential equation

11. The number of arbitrary constants in the solution is equal to the order of the differential equation
Example-2: Let 𝑦 = 𝐴 cos 𝑥 + 𝐵 sin 𝑥 … … (𝑖)
Then differentiating (i) on both sides w.r.t x, we get
𝑑𝑦
𝑑𝑥
= −𝐴 sin 𝑥 + 𝐵 cos 𝑥 … … (𝑖𝑖)
Again differentiating (ii) on both sides w.r.t x, we get
𝑑2 𝑦
𝑑𝑥2
= −𝐴 cos 𝑥 − 𝐵 sin 𝑥 = − 𝐴 cos 𝑥 + 𝐵 sin 𝑥 = −𝑦
𝑜𝑟,
𝑑2
𝑦
𝑑𝑥2
+ 𝑦 = 0
Which is a differential equation of order 2.The number of arbitrary constants in (i) is 2
Therefore, number of arbitrary constants in the solution =the order of the differential equation