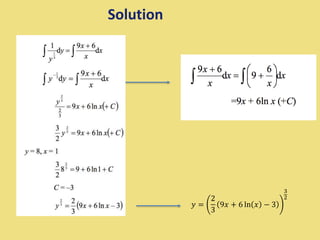
This document provides information about solving first-order differential equations. It discusses the order of differential equations and gives examples of first-order equations. It also describes methods for solving separable and exact first-order differential equations, including separating variables, integrating, and finding particular solutions given initial conditions. Solving differential equations may require integration techniques like substitution, parts, and trigonometric identities.

1. At the end of this lesson you should be able to:
• Solve First Order Differential Equations
FC311 – Intermediate Maths

2. Differential equations
In this course we will mainly be looking at first-order differential equations.
A differential equation in two variables x and y is an equation that contains derivatives of y
with respect to x. For example:
2
= 4 +1,
dy
x
dx
3
= ,
dy
xy
dx
2 + = 5 .
dy
x y xy
dx
The order of a differential equation is given by the highest order of derivative that occurs in
it.
First-order differential equations contain terms in ,
dy
dx
second-order differential equations contain terms in ,
2
2
d y
dx
third-order differential equations contain terms in , etc.
3
3
d y
dx

3. Differential equations
For example, suppose we have the differential equation:
The solution to a differential equation in x and y will take the form y = f(x).
The simplest differential equations are those of the form:
f
= ( )
dy
x
dx
Differential equations of this form can be solved by integrating both sides with respect to x
to give:
f
= ( )
y x dx

= 4 +1
dy
x
dx

4. Differential equations of the form = f(x)
Integrating both sides with respect to x gives:
dy
dx
= (4 +1)
y x dx

2
= 2 + +
y x x c
Since the constant c can take any value, this represents a whole family of solutions as
shown here: 𝑦 = 2𝑥2
+ 𝑥 + 17. 𝑦 = 2𝑥2
+ 𝑥 − 4011. 𝑦 = 2𝑥2
+ 𝑥 − 𝜋
These are just three examples. There are an infinite number of possibilities
This is called the general solution
to the equation .
dy
x
dx
= 4 +1

5. Finding a particular solution
Suppose that as well as being given the differential equation:
Substituting x = 1 and y = 4:
we are also told that when x = 1, y = 4.
We can use this additional information to find the value of the arbitrary constant c in the
general solution:
y x x c
2
= 2 + +
4 = 2 + 1 + c
c = 1
This gives us the particular solution: y x x
2
= 2 + +1
= 4 +1
dy
x
dx

6. Solving first-order differential equations
Find the particular solution to the differential equation
given that y = 6 when x = 0.
Divide both sides by (x2 + 1):
Integrate both sides with respect to x:
dy
x x
dx
2
( +1) = 4
2
4
=
+1
dy x
dx x
x
y
x
 2
2
= 2
+1
y x c
2
= 2ln( +1)+
We can use brackets
because x2 + 1 > 0.
Writing the quotient
in the form .
f
f
'( )
( )
x
x

7. Solving first-order differential equations
Substitute x = 0 and y = 6:
The particular solution is therefore:
c
6 = 2ln(1)+
c = 6
y x2
= 2ln( +1)+6

8. Separating variables
Differential equations that can be arranged in the form
can be solved by the method of separating the variables.
This method works by collecting all the terms in y, including the ‘dy’, on one side of the
equation, and all the terms in x, including the ‘dx’, on the other side, and then integrating.
f g
( ) = ( )
dy
y x
dx
f g
( ) = ( )
y dy x dx
 
f g
( ) = ( )
y dy x dx

9. Separating variables
Find the general solution to .
+ 2
=
dy x
dx y
= ( + 2)
y dy x dx
 
2 2
= + 2 +
2 2
y x
x c
2 2
= + 4 +
y x x A
We only need a ‘c’ on
one side of the equation.
You can miss out the step
and use the fact that
to separate the dy from the
dx directly.
... =...
dy
dx dy
dx
= ( + 2)
dy
y dx x dx
dx
 
2
= + 4 +
y x x A
Separate the variables and integrate:
Rearrange to give: = + 2
dy
y x
dx
It doesn’t make much
sense to have “2𝑐” since
𝑐 is just a constant who’s
value we don’t know. So
we will replace 2𝑐 with 𝐴

10. Separable variables
Separating the variables and integrating with respect to x gives:
3
=
y x
e dy e dx
 
3
1
3
= +
y x
e e c
Using the laws of indices this can be written as:
3
= x y
dy
e e
dx

3
1
3
= ln( + )
x
y e c
Rearrange to get 𝑦, by taking the natural logarithms of both
sides:
Find the particular solution to the differential equation
given that y = ln when x = 0.
3
= x y
dy
e
dx

7
3

11. Separable variables
The particular solution is therefore:
Given that y = ln when x = 0:
7
3
7 1
3 3
ln = ln( + )
c
= 2
c
3
1
3
= ln( +2)
x
y e

12. Your turn
Find the particular solution to the following differential equation, where
𝑦 = 8 at 𝑥 = 1
𝑑𝑦
𝑑𝑥
=
9𝑥 + 6 𝑦
1
3
𝑥

13. Solution
𝑦 =
2
3
9𝑥 + 6 ln 𝑥 − 3
3
2

14. To solve differential equations, we may have to
use any one ( or possibly more than one) of the
integration techniques we have learned.
• Integration by substitution
• Integration by parts
• Integration by partial fractions
• Integration with trig identities
•
𝑓′(𝑥)
𝑓(𝑥)
𝑑𝑥 = ln 𝑓 𝑥 + 𝑐
• (the formula sheet)

15. We also need to rearrange to write our answer
in the form y=f(x) unless a question tells us
otherwise.

16. Example find the general solution for :
cos(𝑥)
𝑑𝑦
𝑑𝑥
=
𝑦𝑥
𝑐𝑜𝑠(𝑥)
1
𝑦
𝑑𝑦 =
𝑥
𝑐𝑜𝑠2(𝑥)
𝑑𝑥
1
𝑦
𝑑𝑦 = 𝑥𝑠𝑒𝑐2𝑥𝑑𝑥
ln 𝑦 = 𝑥𝑡𝑎𝑛𝑥 − 𝑡𝑎𝑛𝑥𝑑𝑥
To solve the RHS, we must
use integration by parts
ln 𝑦 = 𝑥𝑡𝑎𝑛𝑥 − 𝑙𝑛 sec 𝑥 + 𝑐
ln 𝑦 = 𝑥𝑡𝑎𝑛𝑥 + 𝑙𝑛 cos 𝑥 + 𝑐
Use the power rule, to take
-1 inside the logarithm

17. Example find the general solution for :
cos(𝑥)
𝑑𝑦
𝑑𝑥
=
𝑦𝑥
𝑐𝑜𝑠(𝑥)
ln 𝑦 = 𝑥𝑡𝑎𝑛𝑥 + 𝑙𝑛 cos 𝑥 + 𝑐
𝑦 = 𝑒𝑥𝑡𝑎𝑛𝑥+𝑙𝑛 cos 𝑥 +𝑐
𝑦 = 𝑒𝑥𝑡𝑎𝑛𝑥 × 𝑒𝑙𝑛 cos 𝑥 × 𝑒𝑐
Use the laws of indices
to separate the powers.
Now 𝑒𝑐
, is just a
constant, so we can call
it 𝐴.
𝑦 = 𝐴 cos 𝑥 𝑒𝑥𝑡𝑎𝑛𝑥
This is the simplest way
to give the solution.