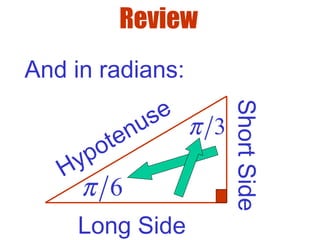
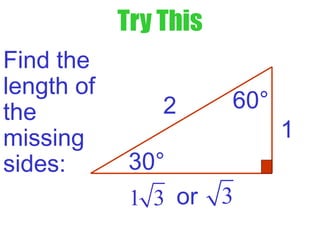
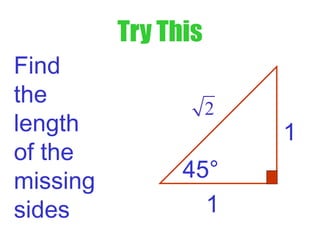
1) The document discusses inverse trigonometric functions such as arcsin, arccos, and arctan. It reviews special angle identities and defines the inverse trig functions. 2) Examples are provided to demonstrate evaluating inverse trig functions and writing equations in inverse form. The principal values of inverse trig functions are defined as being between -90 and 90 degrees. 3) The document contains examples of using inverse trig functions to find missing side lengths in 30-60-90 and 45-45-90 triangles based on special angle identities, as well as evaluating expressions involving inverse trig functions.

1. 8.2: Inverse Trig Functions
© 2008 Roy L. Gover(www.mrgover.com)
Learning Goals:
•Review Special Angles
•Evaluate inverse trig
functions.

2. Review
The special angles are:
6
π
3
π
60° or
4
π
45° or
30° or

3. Consider the first two
special angles in degrees...
30°
60°
Long Side ShortSide
Hypotenuse
Review

4. And in radians:
Long Side ShortSide
Hypotenuse
Review
6π
3π

5. Important Idea
In a 30° ,60° ,
triangle:
•the short side is one-half
the hypotenuse.
•the long side is times
the short side.
3
( 6)π ( 3)π
( 2)π90°

6. Important Idea
In a 45° ,45° ,90°
triangle:
•The legs of the triangle
are equal.
•the hypotenuse is
times the length of the leg.
2
( 4)π ( 4)π
( 2)π

7. Try This
Find the
length of
the
missing
sides: 30°
60°
1
2
1 3 or 3

8. Try This
Find
the
length
of the
missing
sides 1
1
2
45°

9. Important Idea
Many trig functions can be
solved without graphing by
using special angles and
inverse trig functions. A
special angle solution will be
an exact solution whereas a
graphing solution is only
approximate.

10. Definition
Trig
Function
Inverse Trig Function
siny x= 1
sinx y−
=
cosy x= 1
cosx y−
=
tany x= 1
tanx y−
=

11. Important Idea
arcsin y
arccos y
arctan y
In some books:
1
sin y−
1
cos y−
1
tan y−
instead of
instead of
instead of

12. Example
Find the exact value
without using a calculator;
1 1
sin
2
− 1 2
cos
2
− ( )1
sin 1−
−
1
tan (1)− 1 3
cos
2
−  
− ÷
 

13. Example
Find all values of x in the
interval for
which:
2
cos
2
x =
0 360x° ≤ ≤ °

14. Example
Find all values of x in the
interval for
which:
2
cos
2
x =
0 2x π≤ ≤

15. Try This
Find all values of x in the
interval for
which: 1
sin
2
x = −
0 360x° ≤ ≤ °
210 & 330x = ° °

16. Try This
Find all values of x in the
interval for
which tan 1x =
0 360x° ≤ ≤ °
45 & 225x = ° °
Hint: in what quadrants is
the tangent positive?

17. Example
Write each equation in the
form of an inverse relation:
4
tan
5
α=

18. Example
Write each equation in the
form of an inverse relation:
1
cos
3
β =

19. Try This
Write each equation in the
form of an inverse relation:
sin 1x =
1
sin 1 or arcsin1x x−
= =

20. Example
Find the value of x in the
for which:
cos .6328x =
Leave your answer in
degrees to the nearest tenth.

21. Try This
Find the value of x in the
for which: sin .6328x =
Leave your answer in
degrees to the nearest tenth.
x=39.3
Can you find another value
for x?

22. Definition
The calculator will provide
only the Principal Values of
inverse trig functions:
1
sin x−
1
cos x−
1
tan ( )x−
[ ]90 ,90− ° °
[ ]2, 2π π−
[ ]0,180° [ ]0,πor
or

23. Example
Evaluate the expression.
Assume all angles are in
quadrant 1.
1
sin arcsin
2
 
 ÷
 

24. Example
Evaluate the expression.
Assume all angles are in
quadrant 1.
3
sin arccos
2
 
 ÷ ÷
 

25. Try This
Evaluate the expression.
Assume all angles are in
quadrant 1.
1
os arcsinc
2
 
 ÷
 
3
2

26. Racetrack curves are banked so
that cars can make turns at high
speeds. The proper banking
angle,θ, is given by: 2
tan
v
gr
θ =
where v is the velocity of the car,
g is the acceleration of gravity &
r is the radius of the turn. Find θ
when r=1000ft & v=180 mph.
Example

27. Lesson Close
In order to have an inverse
trig function, we must
restrict the domain so that
duplicate values are
eliminated.