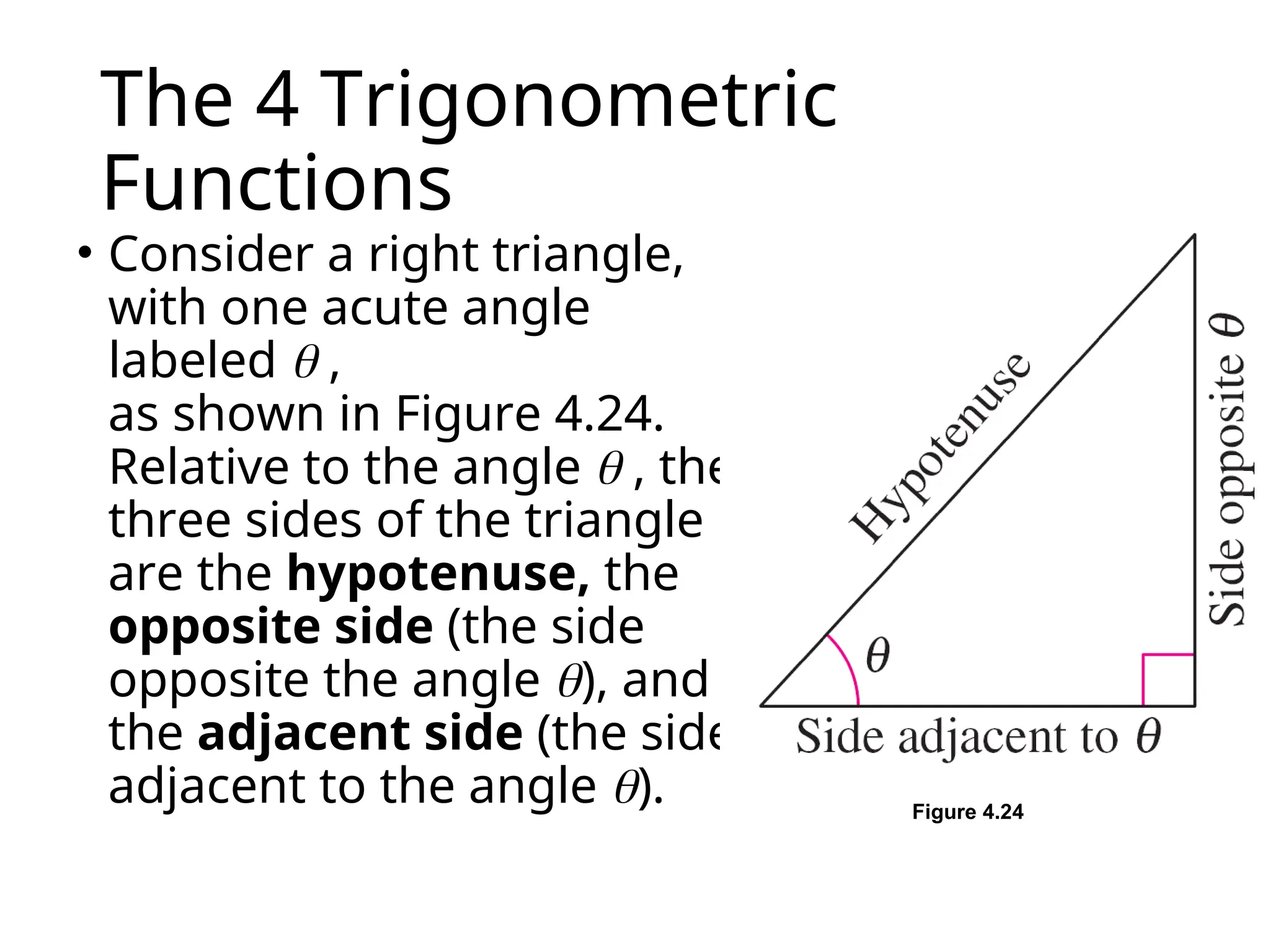
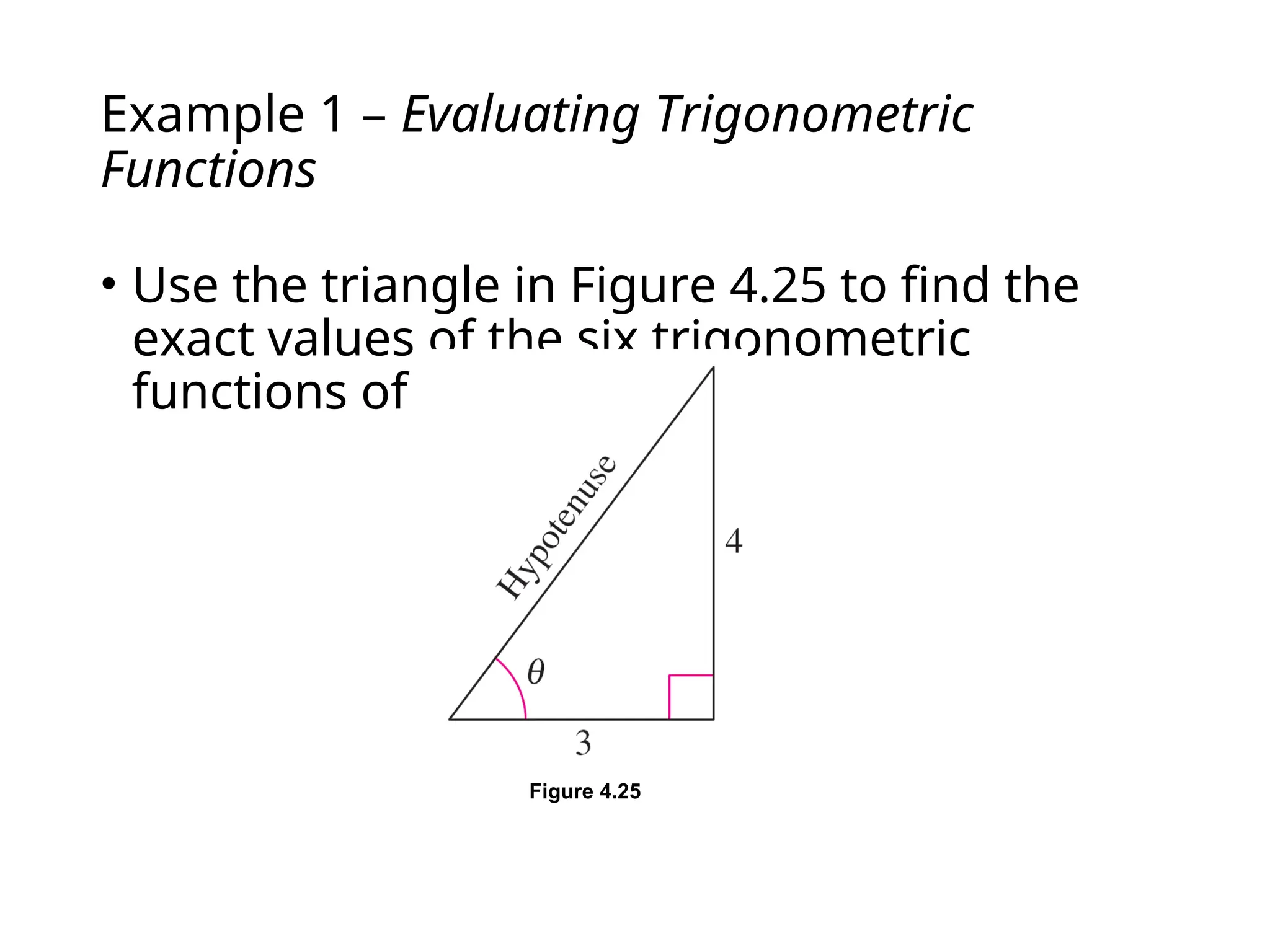
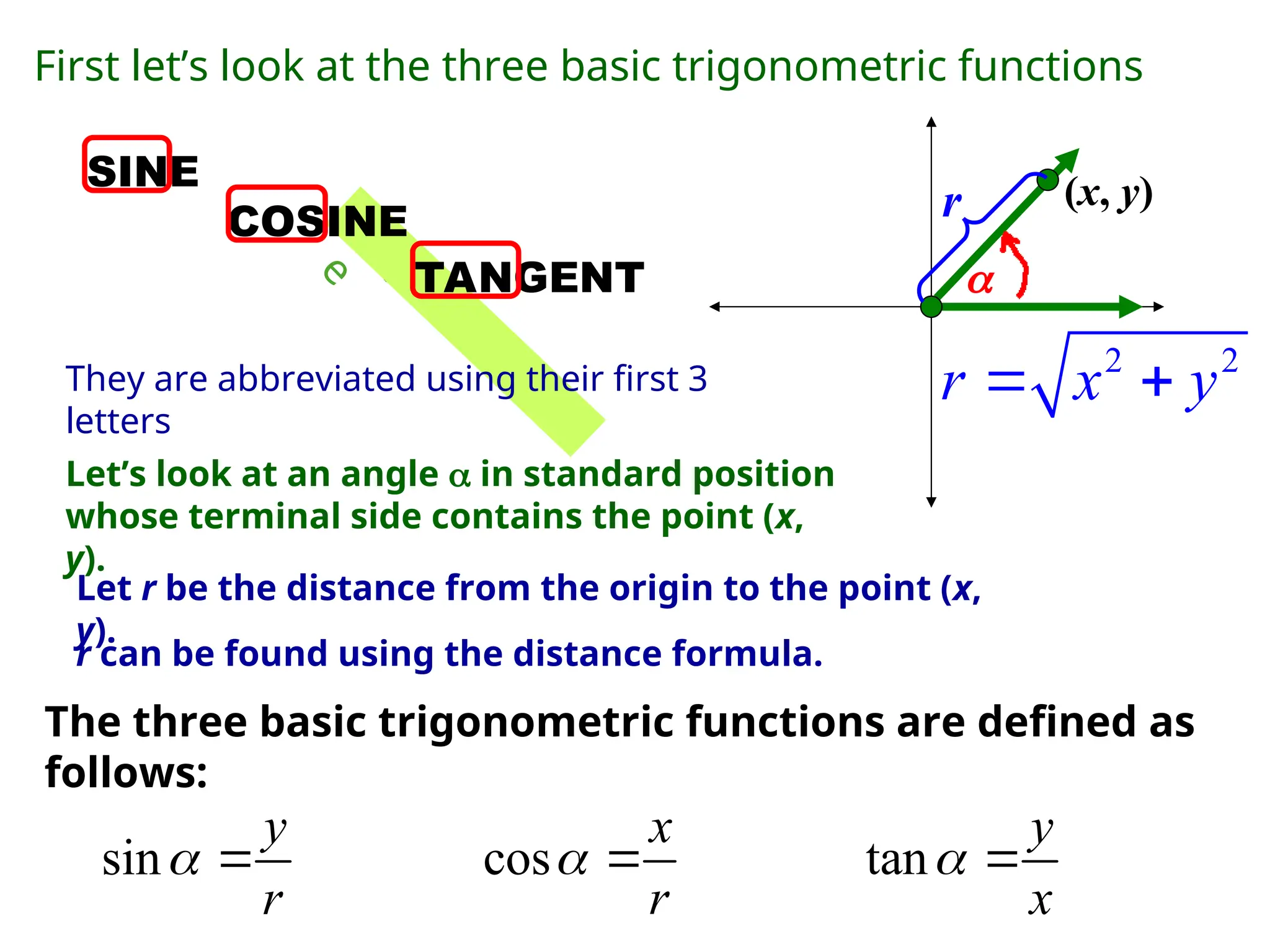
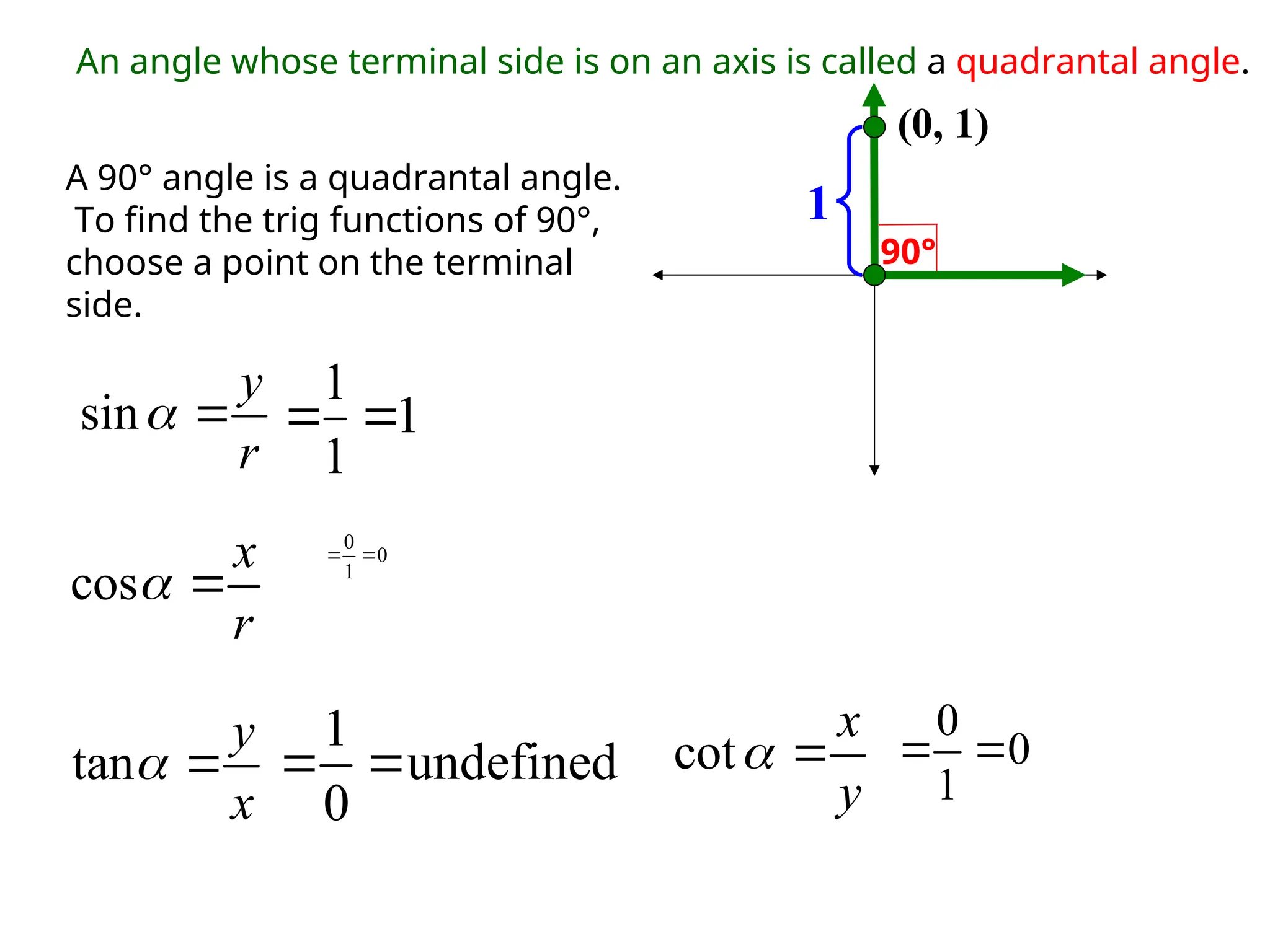
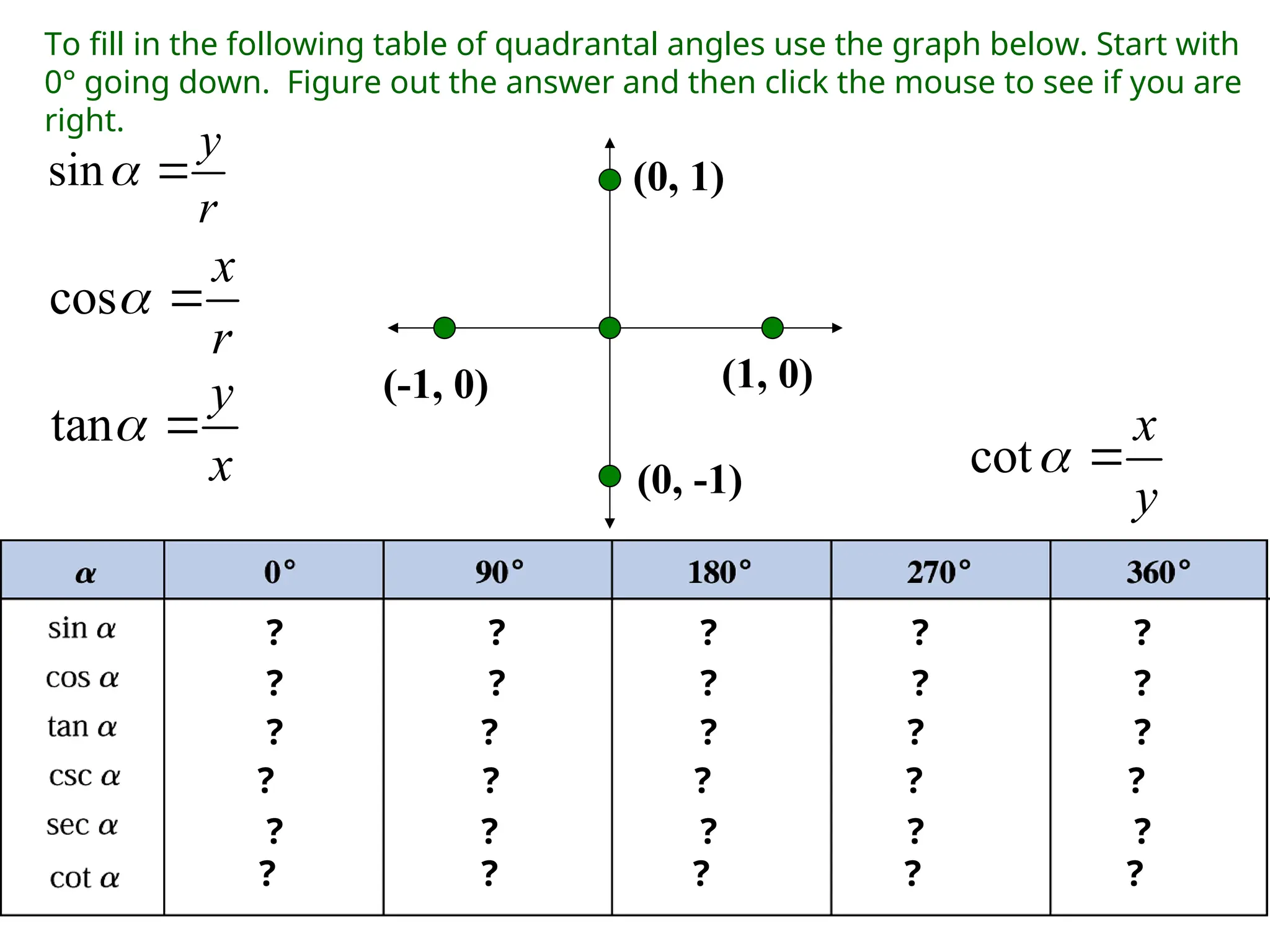
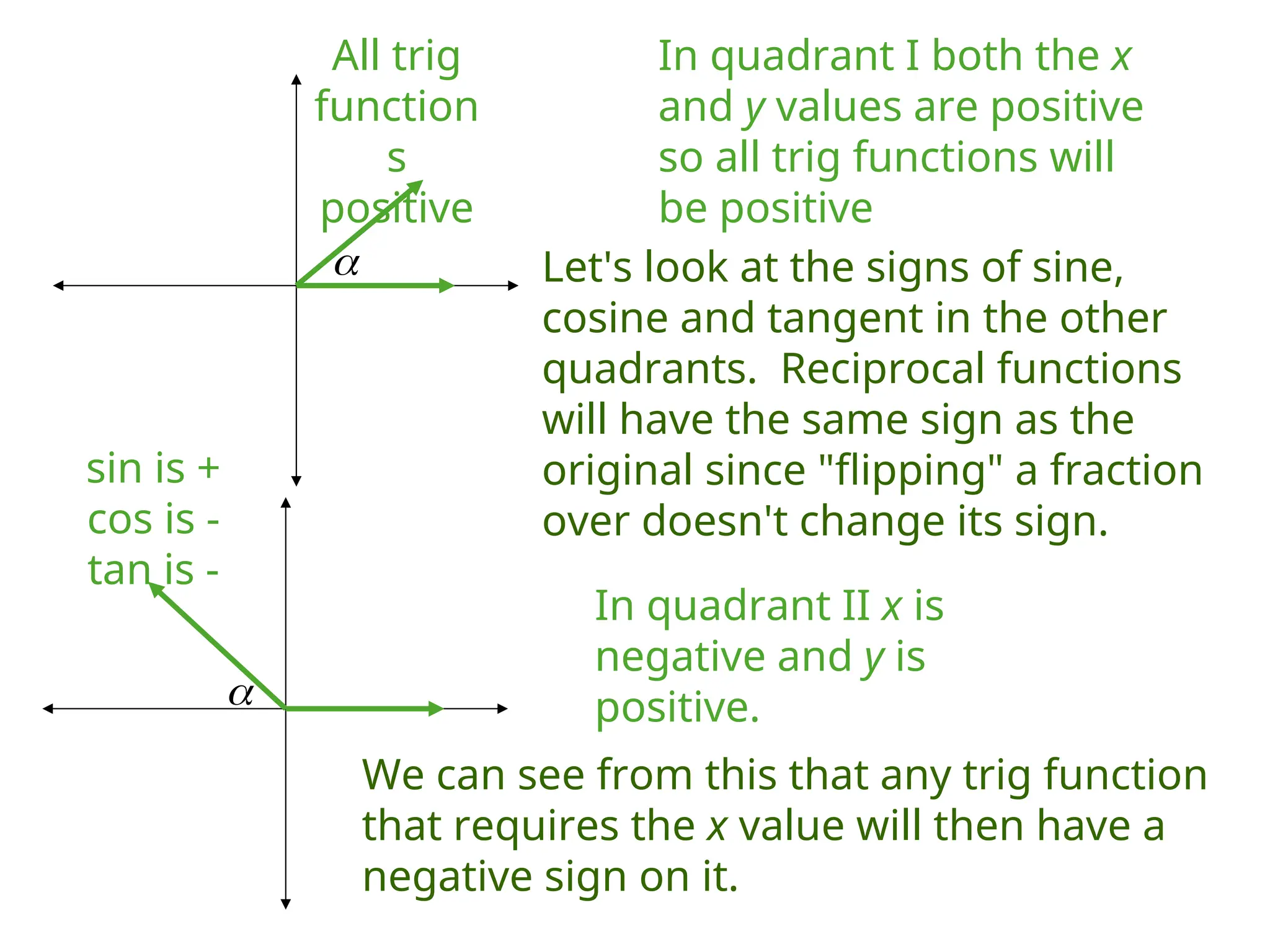
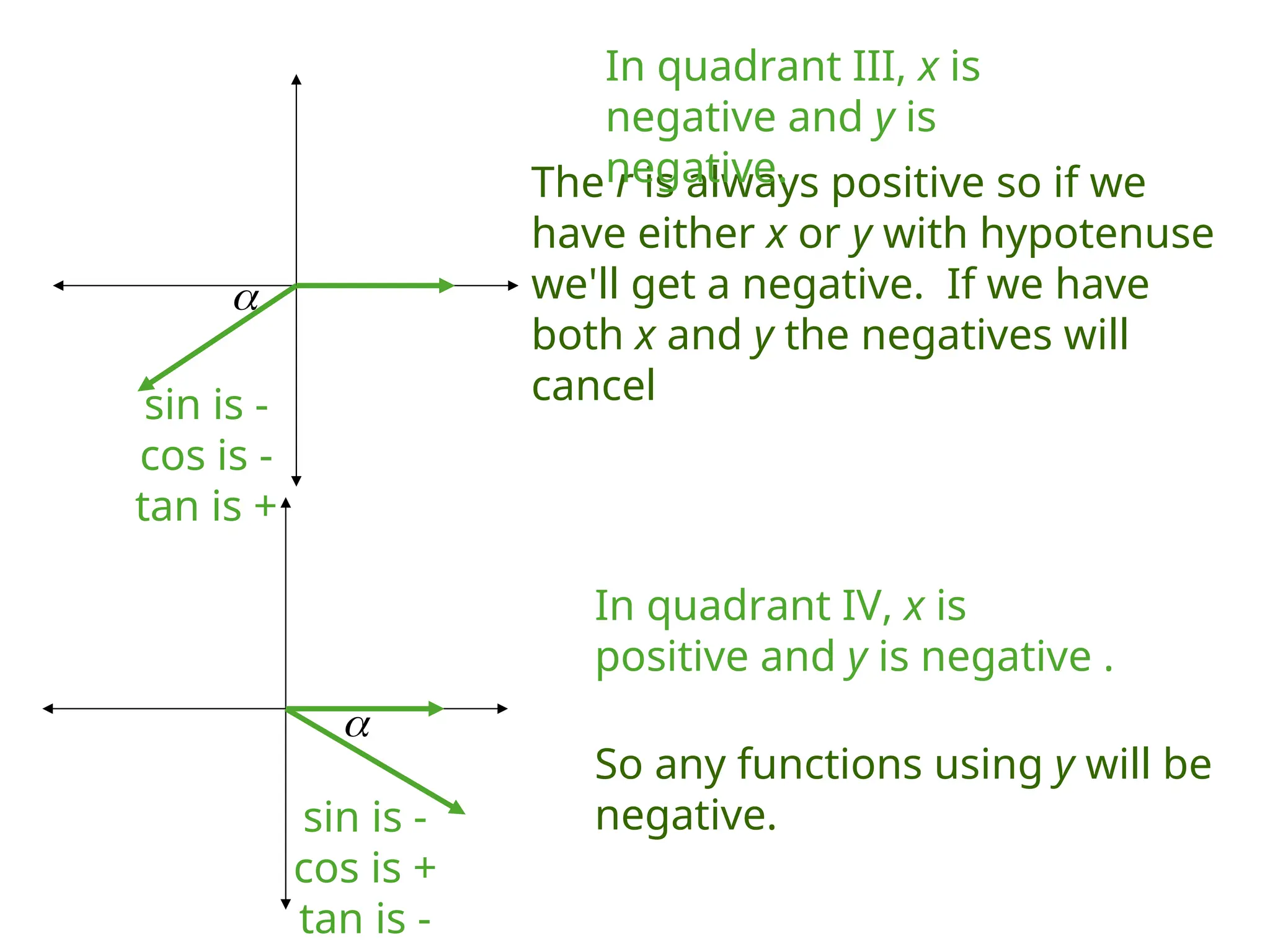
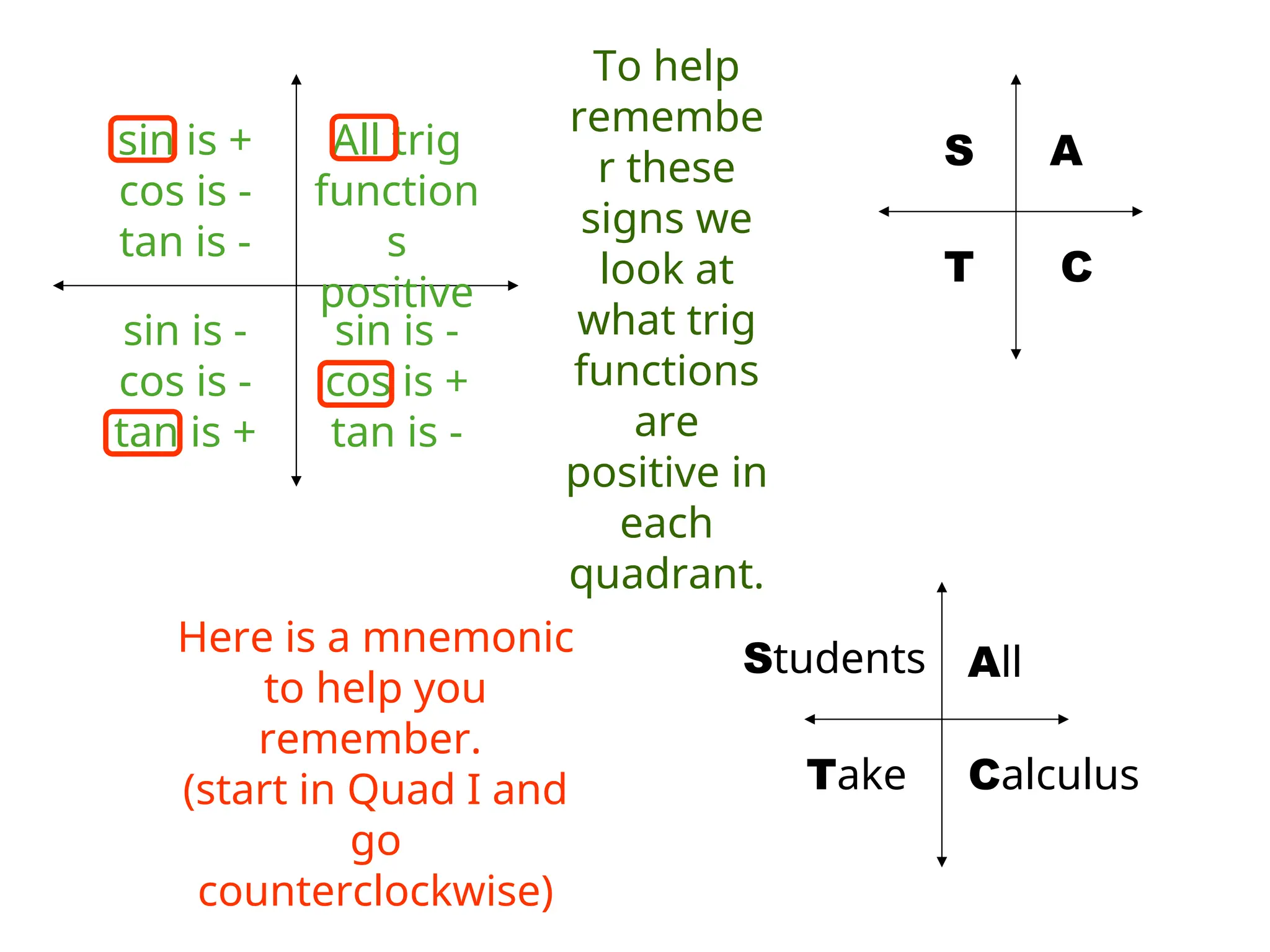
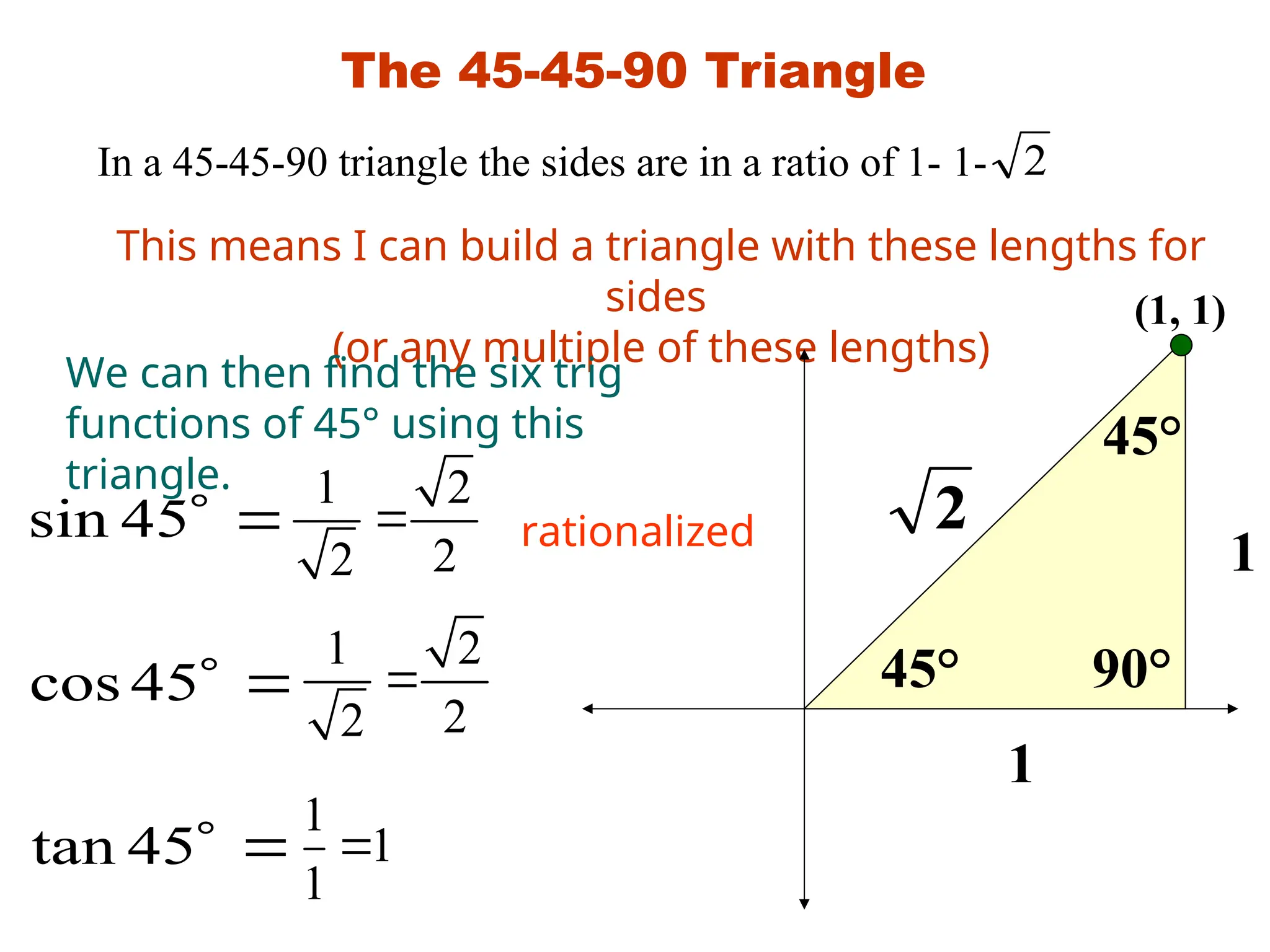
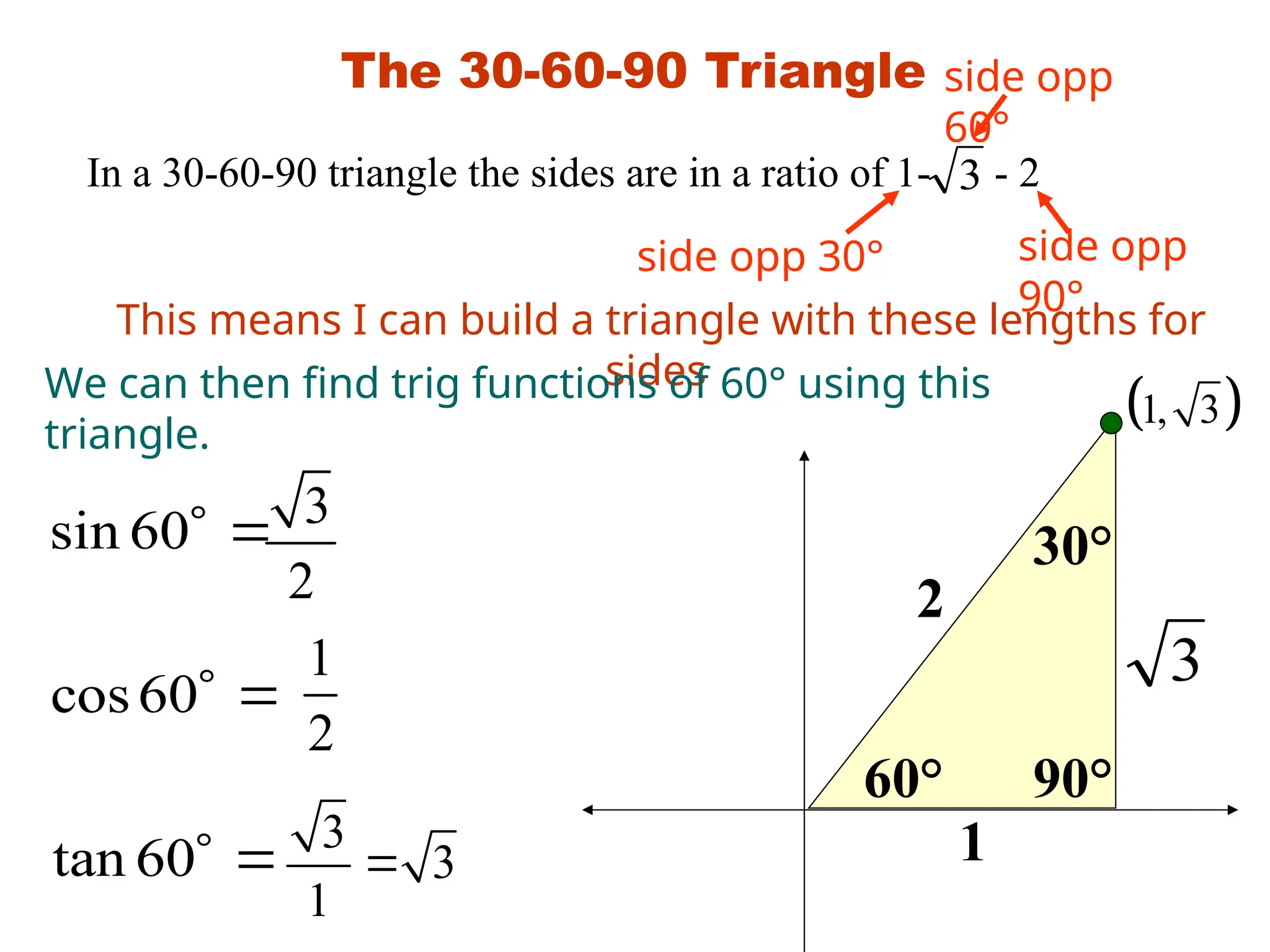
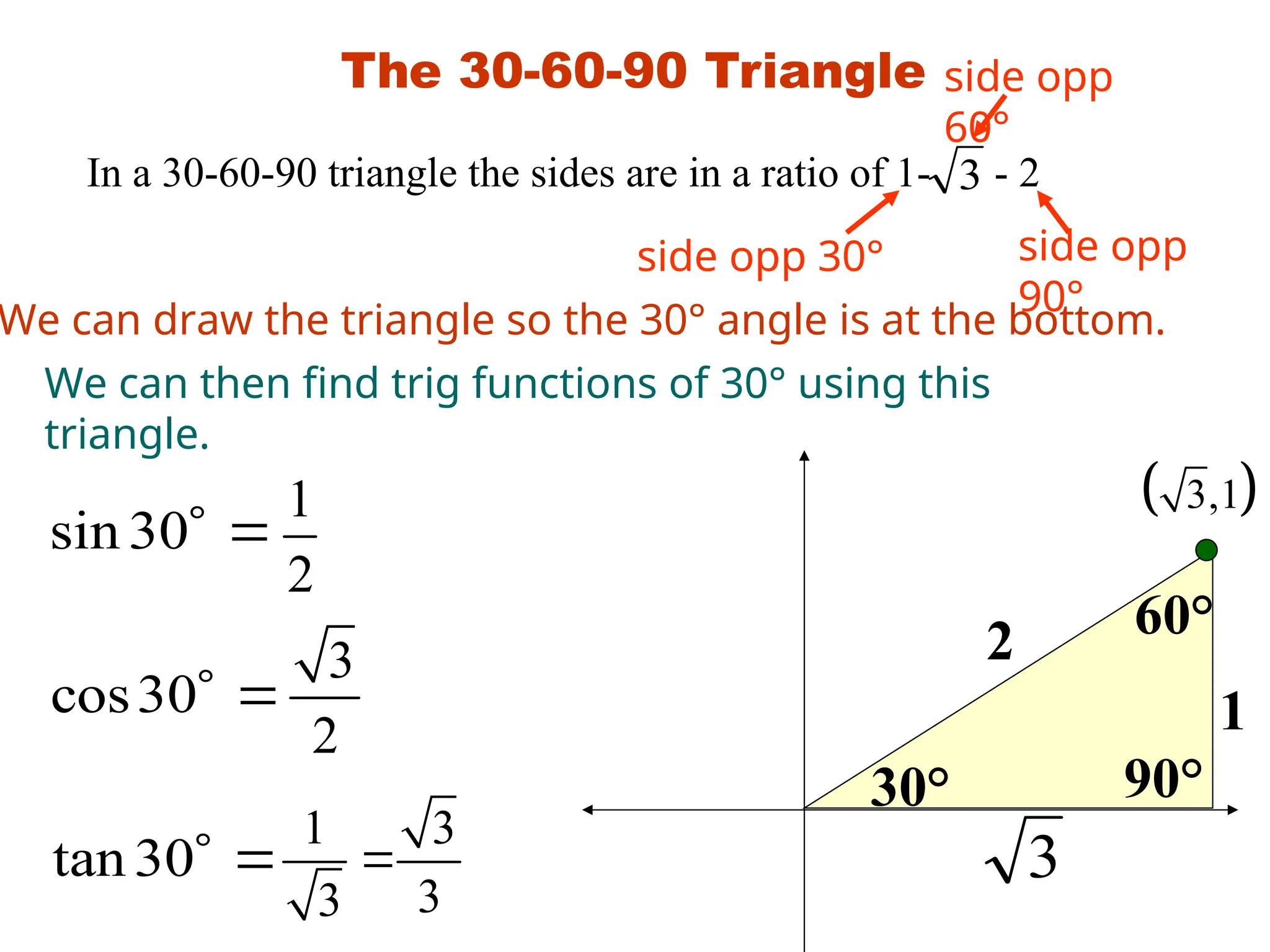
The document covers trigonometric functions, focusing on the definitions and relationships of sine, cosine, and tangent for angles in a right triangle and on a unit circle. It explains how to evaluate these functions using specific triangles such as the 45-45-90 and 30-60-90 triangles, including the associated ratios and properties in quadrants. Additionally, it discusses the use of calculators for finding sine and reciprocal functions and emphasizes the importance of knowing exact values for common angles.

1. The
Trigonometric
Functions

2. 9.2.4.1 learn definitions of
trigonometric functions; 9.2.4.2 learn
the relation of coordinates (cosα;sin α
) on a unit circle using trigonometric
functions;

3. The 4 Trigonometric
Functions
• Consider a right triangle,
with one acute angle
labeled  ,
as shown in Figure 4.24.
Relative to the angle  , the
three sides of the triangle
are the hypotenuse, the
opposite side (the side
opposite the angle ), and
the adjacent side (the side
adjacent to the angle ). Figure 4.24

4. The 4 Trigonometric
Functions
• Using the lengths of these three sides, you can form four
ratios that define the six trigonometric functions of the
acute angle .
• sine
• cosine
• tangent
• cotangent
• In the following definitions it is important to see that
• 0 <  < 90
• and that for such angles the value of each trigonometric
function is positive.
 lies in the first quadrant

5. The 4 Trigonometric
Functions

6. Example 1 – Evaluating Trigonometric
Functions
• Use the triangle in Figure 4.25 to find the
exact values of the six trigonometric
functions of .
Figure 4.25

7. Example 1 – Solution
• By the Pythagorean Theorem,(hyp)2
= (opp)2
+ (adj)2
,
it follows that
• hyp =
• =
• = 5.
cont’d

8. Example 1 – Solution
• So, the trigonometric functions of  are
cont’d

9. h
y
p
o
t
e
n
u
s
e
First let’s look at the three basic trigonometric functions
SINE
COSINE
TANGENT
They are abbreviated using their first 3
letters
sin
y
r
  cos
x
r
  tan
y
x
 
Let’s look at an angle  in standard position
whose terminal side contains the point (x,
y).

(x, y)
r
2 2
r x y
 
The three basic trigonometric functions are defined as
follows:
Let r be the distance from the origin to the point (x,
y).
r can be found using the distance formula.

10. Find the values of the six trigonometric functions of the
angle  in standard position whose terminal side passes
through the point (4, -5)
(4, -5)
r

   
2 2
4 5
r    41

41
sin
y
r
 
cos
x
r
 
tan
y
x
  cot
x
y
 
5
41

4
41

5
4

4
5

Often the
preferred way
to leave the
answer is with
a rationalized
denominator
41
41
 5 41
41

41
41
 4 41
41


11. An angle whose terminal side is on an axis is called a quadrantal angle.
A 90° angle is a quadrantal angle.
To find the trig functions of 90°,
choose a point on the terminal
side.
90°
(0, 1)
1
sin
y
r
 
cos
x
r
 
tan
y
x
  cot
x
y
 
1
1
1
 
0
0
1
 
1
undefined
0
 
0
0
1
 

12. To fill in the following table of quadrantal angles use the graph below. Start with
0° going down. Figure out the answer and then click the mouse to see if you are
right.
(0, 1)
sin
y
r
 
cos
x
r
 
tan
y
x
 
cot
x
y
 
(1, 0)
(0, -1)
(-1, 0)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?

13. In quadrant I both the x
and y values are positive
so all trig functions will
be positive

All trig
function
s
positive
In quadrant II x is
negative and y is
positive.

We can see from this that any trig function
that requires the x value will then have a
negative sign on it.
Let's look at the signs of sine,
cosine and tangent in the other
quadrants. Reciprocal functions
will have the same sign as the
original since "flipping" a fraction
over doesn't change its sign.
sin is +
cos is -
tan is -

14. 
In quadrant IV, x is
positive and y is negative .

So any functions using y will be
negative.
The r is always positive so if we
have either x or y with hypotenuse
we'll get a negative. If we have
both x and y the negatives will
cancel
sin is -
cos is +
tan is -
In quadrant III, x is
negative and y is
negative.
sin is -
cos is -
tan is +

15. All trig
function
s
positive
sin is +
cos is -
tan is -
sin is -
cos is +
tan is -
sin is -
cos is -
tan is +
To help
remembe
r these
signs we
look at
what trig
functions
are
positive in
each
quadrant.
A
S
T C
Here is a mnemonic
to help you
remember.
(start in Quad I and
go
counterclockwise)
All
Students
Take Calculus

16. S
P
E
C
I
A
L
U
S
I
N
G
TRIANGLES
Computing the Values of Trig
Functions of Acute Angles

17. The 45-45-90 Triangle
In a 45-45-90 triangle the sides are in a ratio of 1- 1- 2
This means I can build a triangle with these lengths for
sides
(or any multiple of these lengths)
45°
45°
90°
1
1
2
We can then find the six trig
functions of 45° using this
triangle.






45
tan
45
cos
45
sin
1 2
2
2

1 2
2
2

rationalized
1
1
1

(1, 1)

18. You are expected to know exact values for trig functions of
45°. You can get them by drawing the triangle and using
sides.
45°
45°
90°
1
1
2
What is the radian equivalent of 45°?


4
tan
4
sec


1
1
1

You also know all the trig
functions for /4 then.
4


19. The 30-60-90 Triangle
In a 30-60-90 triangle the sides are in a ratio of 1- - 2
3
This means I can build a triangle with these lengths for
sides
60°
30°
90°
2
1
3
We can then find trig functions of 60° using this
triangle.
sin 60
cos60
tan 60
 
 
 
3
2
1
2
3
3
1

side opp
60°
side opp 30° side opp
90°
 
1, 3

20. The 30-60-90 Triangle
In a 30-60-90 triangle the sides are in a ratio of 1- - 2
3
We can draw the triangle so the 30° angle is at the bottom.
30°
60°
90°
2
1
3
We can then find trig functions of 30° using this
triangle.
sin 30
cos30
tan 30
 
 
 
3
2
1
2
1 3
3
3

side opp
60°
side opp 30° side opp
90°
 
3,1

21. What this means is that if you memorize the special
triangles, then you can find all of the trig functions of 45°,
30°, and 60° which are common ones you need to know.
You also can find the radian equivalents of these angles.
4
45



6
30



3
60



When directions say "Find the exact value", you
must know these values not a decimal
approximation that your calculator gives you.

22. Here is a table of sines and cosines for common
angles. You can get these by drawing the special
triangles, but notice the pattern.

24. What did you learn?
What part of the lesson was the most
difficult for you?

25. Using a Calculator to Find
Values of Trig Functions
If we wanted sin 38° we could not use
the previous methods to find it
because we don't know the lengths of
sides of a triangle with a 38° angle. We
will then use our calculator to
approximate the value.
You can simply use the sin button on
the calculator followed by (38) to find
the sin 38°
A word to the wise: Always make sure your calculator is in
the right mode for the type of angle you have (degrees or
radians). If there is not a degree symbol then you know the
angle is in radians.

26. Using a Calculator to Find
Values of Reciprocal Trig
Functions
If we wanted csc (/5) we use our
calculator to approximate the value
remembering that cosecant is the
reciprocal function of sine so is
1 over sine.
You can simply put in 1 divided by sin
followed by (/5 ) to find the csc /5
Make sure you are in radian mode
and that you put the /5 in
parenthesis.

27. HW