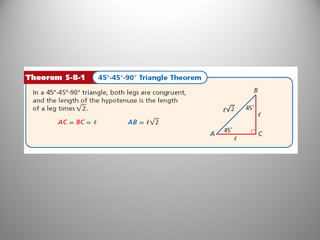
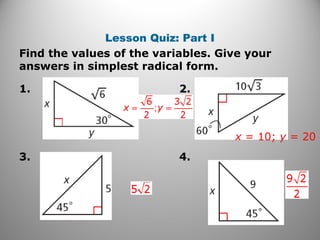
This document provides instruction on using 45-45-90 and 30-60-90 right triangles to solve problems. It includes examples of finding missing side lengths, using the relationships between sides, and applying the triangles to real-world situations like cutting fabric and designing ornaments. Practice problems are provided to have students demonstrate their understanding of using these special right triangles.

1. UUNNIITT 88..22 SSPPEECCIIAALL RRIIGGHHTT
TTRRIIAANNGGLLEESS

2. Warm Up
For Exercises 1 and 2, find the value of x.
Give your answer in simplest radical form.
1. 2.
Simplify each expression.
3. 4.

3. Objectives
Justify and apply properties of
45°-45°-90° triangles.
Justify and apply properties of
30°- 60°- 90° triangles.

4. A diagonal of a square divides it into two congruent
isosceles right triangles. Since the base angles of an
isosceles triangle are congruent, the measure of
each acute angle is 45°. So another name for an
isosceles right triangle is a 45°-45°-90° triangle.
A 45°-45°-90° triangle is one type of special right
triangle. You can use the Pythagorean Theorem to
find a relationship among the side lengths of a 45°-
45°-90° triangle.

6. Example 1A: Finding Side Lengths in a 45°- 45º- 90º
Triangle
Find the value of x. Give your
answer in simplest radical form.
By the Triangle Sum Theorem, the
measure of the third angle in the
triangle is 45°. So it is a 45°-45°-
90° triangle with a leg length of 8.

7. Example 1B: Finding Side Lengths in a 45º- 45º- 90º
Triangle
Find the value of x. Give your
answer in simplest radical form.
The triangle is an isosceles right
triangle, which is a 45°-45°-90°
triangle. The length of the hypotenuse
is 5.
Rationalize the denominator.

8. Check It Out! Example 1a
Find the value of x. Give your answer in
simplest radical form.
By the Triangle Sum Theorem, the
measure of the third angle in the
triangle is 45°. So it is a 45°-45°-
90° triangle with a leg length of
x = 20 Simplify.

9. Check It Out! Example 1b
Find the value of x. Give your answer in
simplest radical form.
The triangle is an isosceles right
triangle, which is a 45°-45°-90°
triangle. The length of the
hypotenuse is 16.
Rationalize the denominator.

10. Example 2: Craft Application
Jana is cutting a square of material for a
tablecloth. The table’s diagonal is 36 inches.
She wants the diagonal of the tablecloth to be
an extra 10 inches so it will hang over the
edges of the table. What size square should
Jana cut to make the tablecloth? Round to the
nearest inch.
Jana needs a 45°-45°-90° triangle with a hypotenuse
of 36 + 10 = 46 inches.

11. Check It Out! Example 2
What if...? Tessa’s other dog is wearing a
square bandana with a side length of 42 cm.
What would you expect the circumference of
the other dog’s neck to be? Round to the
nearest centimeter.
Tessa needs a 45°-45°-90° triangle with a
hypotenuse of 42 cm.

12. A 30°-60°-90° triangle is another special right
triangle. You can use an equilateral triangle to find
a relationship between its side lengths.

13. Example 3A: Finding Side Lengths in a 30º-60º-90º
Triangle
Find the values of x and y. Give
your answers in simplest
radical form.
22 = 2x Hypotenuse = 2(shorter leg)
11 = x Divide both sides by 2.
Substitute 11 for x.

14. Example 3B: Finding Side Lengths in a 30º-60º-90º
Triangle
Find the values of x and y. Give your
answers in simplest radical form.
Rationalize the denominator.
Hypotenuse = 2(shorter leg).
Simplify.
y = 2x

15. Check It Out! Example 3a
Find the values of x and y.
Give your answers in simplest
radical form.
Hypotenuse = 2(shorter leg)
Divide both sides by 2.
y = 27 Substitute for x.

16. Check It Out! Example 3b
Find the values of x and y.
Give your answers in simplest
radical form.
Simplify.
y = 2(5)
y = 10

17. Check It Out! Example 3c
Find the values of x and y.
Give your answers in
simplest radical form.
Hypotenuse = 2(shorter leg)
Divide both sides by 2.
Substitute 12 for x.
24 = 2x
12 = x

18. Check It Out! Example 3d
Find the values of x and y.
Give your answers in
simplest radical form.
Rationalize the denominator.
x = 2y Hypotenuse = 2(shorter leg)
Simplify.

19. Example 4: Using the 30º-60º-90º Triangle Theorem
An ornamental pin is in the shape of
an equilateral triangle. The length of
each side is 6 centimeters. Josh will
attach the fastener to the back along
AB. Will the fastener fit if it is 4
centimeters long?
Step 1 The equilateral triangle is divided into two
30°-60°-90° triangles.
The height of the triangle is the length of the
longer leg.

20. Example 4 Continued
Step 2 Find the length x of the shorter leg.
6 = 2x Hypotenuse = 2(shorter leg)
3 = x Divide both sides by 2.
Step 3 Find the length h of the longer leg.
The pin is approximately 5.2 centimeters high.
So the fastener will fit.

21. Check It Out! Example 4
What if…? A manufacturer wants to
make a larger clock with a height of
30 centimeters. What is the length
of each side of the frame? Round to
the nearest tenth.
Step 1 The equilateral triangle is divided into two
30º-60º-90º triangles.
The height of the triangle is the length of the
longer leg.

22. Check It Out! Example 4 Continued
Step 2 Find the length x of the shorter leg.
Rationalize the denominator.
Step 3 Find the length y of the longer leg.
y = 2x Hypotenuse = 2(shorter leg)
Simplify.
Each side is approximately 34.6 cm.

23. Lesson Quiz: Part I
Find the values of the variables. Give your
answers in simplest radical form.
1. 2.
3. 4.
x = 10; y = 20

24. Lesson Quiz: Part II
Find the perimeter and area of each figure.
Give your answers in simplest radical form.
5. a square with diagonal length 20 cm
6. an equilateral triangle with height 24 in.

25. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the Copyright Act
1976, allowance is made for
"fair use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by
copyright statute that might
otherwise be infringing.
Non-profit, EDUCATIONAL or
personal use tips the balance in
favor of fair use.