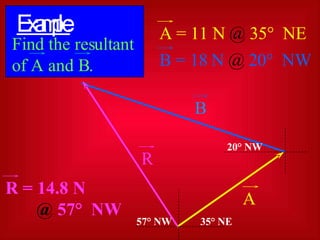
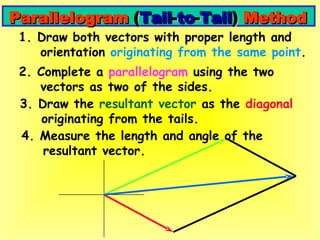
Scalars are quantities that have magnitude only, with no direction. Vectors are quantities that have both magnitude and direction, represented by arrows with length proportional to magnitude and direction the arrow points. Vectors can be added graphically by drawing the first vector and placing the head of the second vector at the tail of the first, with the resultant vector running from the tail of the first to the head of the second. Vectors can also be added analytically by resolving each into x and y components and summing the respective components.

2. Scalar a quantity described by magnitude only examples include: time, length, speed, temperature, mass, energy Vector a quantity described by magnitude and direction examples include: velocity, displacement, force, momentum, electric and magnetic fields

3. Vectors are usually named with capital letters with arrows above the letter. They are represented graphically as arrows. The length of the arrow corresponds to the magnitude of the vector . The direction the arrow points is the vector direction. Examples include: A = 20 m/s at 35 ° NE B = 120 lb at 60 ° SE C = 5.8 mph/s west

4. Vector Addition  vectors may be added graphically or analytically Triangle ( Head - to - Tail ) Method 1. Draw the first vector with the proper length and orientation. 2. Draw the second vector with the proper length and orientation originating from the head of the first vector . 3. The resultant vector is the vector originating at the tail of the first vector and terminating at the head of the second vector . 4. Measure the length and orientation angle of the resultant.

5. Find the resultant of A and B. A = 11 N @ 35 ° NE A 35 ° NE B = 18 N @ 20 ° NW B 20 ° NW R Example: 57 ° NW R = 14.8 N @ 57 ° NW

6. Parallelogram ( Tail - to - Tail ) Method 1. Draw both vectors with proper length and orientation originating from the same point . 2. Complete a parallelogram using the two vectors as two of the sides. 3. Draw the resultant vector as the diagonal originating from the tails. 4. Measure the length and angle of the resultant vector.

7. Explore more vectors at link , link , link , and link .

8. Resolving a Vector Into Components +x +y A A x A y  The horizontal , or x-component , of A is found by A x = A cos   The vertical , or y-component , of A is found by A y = A sin   By the Pythagorean Theorem , A x 2 + A y 2 = A 2 . Every vector can be resolved using these formulas, such that A is the magnitude of A , and  is the angle the vector makes with the x-axis . Each component must have the proper “sign” according to the quadrant the vector terminates in .

9. Analytical Method of Vector Addition 1. Find the x- and y-components of each vector. A x = A cos  = A y = A sin  = B x = B cos  = B y = B sin  = C x = C cos  = C y = C sin  = 2. Sum the x-components. This is the x-component of the resultant. R x = 3. Sum the y-components. This is the y-component of the resultant. R y = 4. Use the Pythagorean Theorem to find the magnitude of the resultant vector. R x 2 + R y 2 = R 2

10. 5. Find the reference angle by taking the inverse tangent of the absolute value of the y-component divided by the x-component .  = Tan -1 R y / R x 6. Use the “signs” of R x and R y to determine the quadrant. NE (+,+) NW (-,+) SW (-,-) SE (-,+)