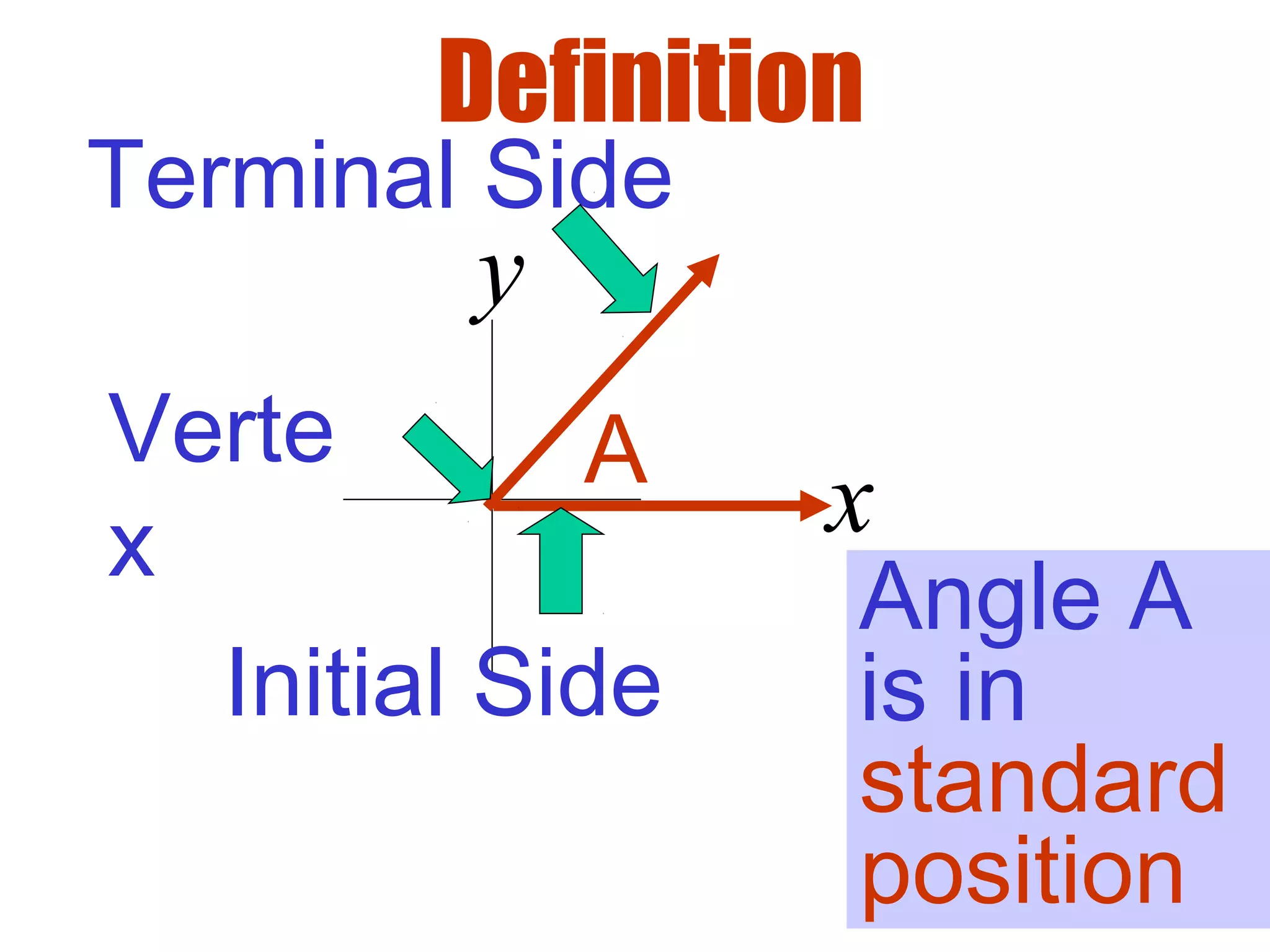
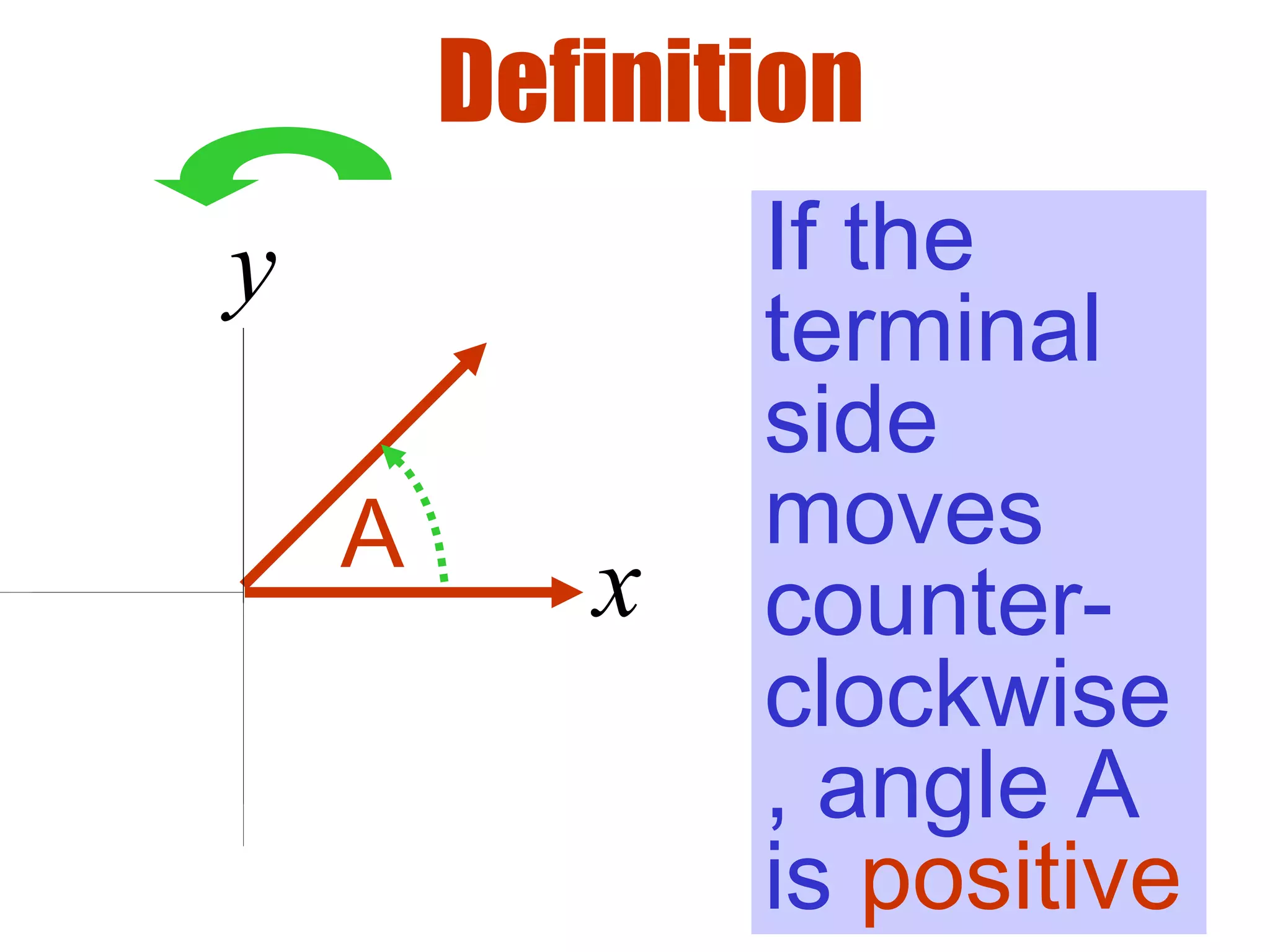
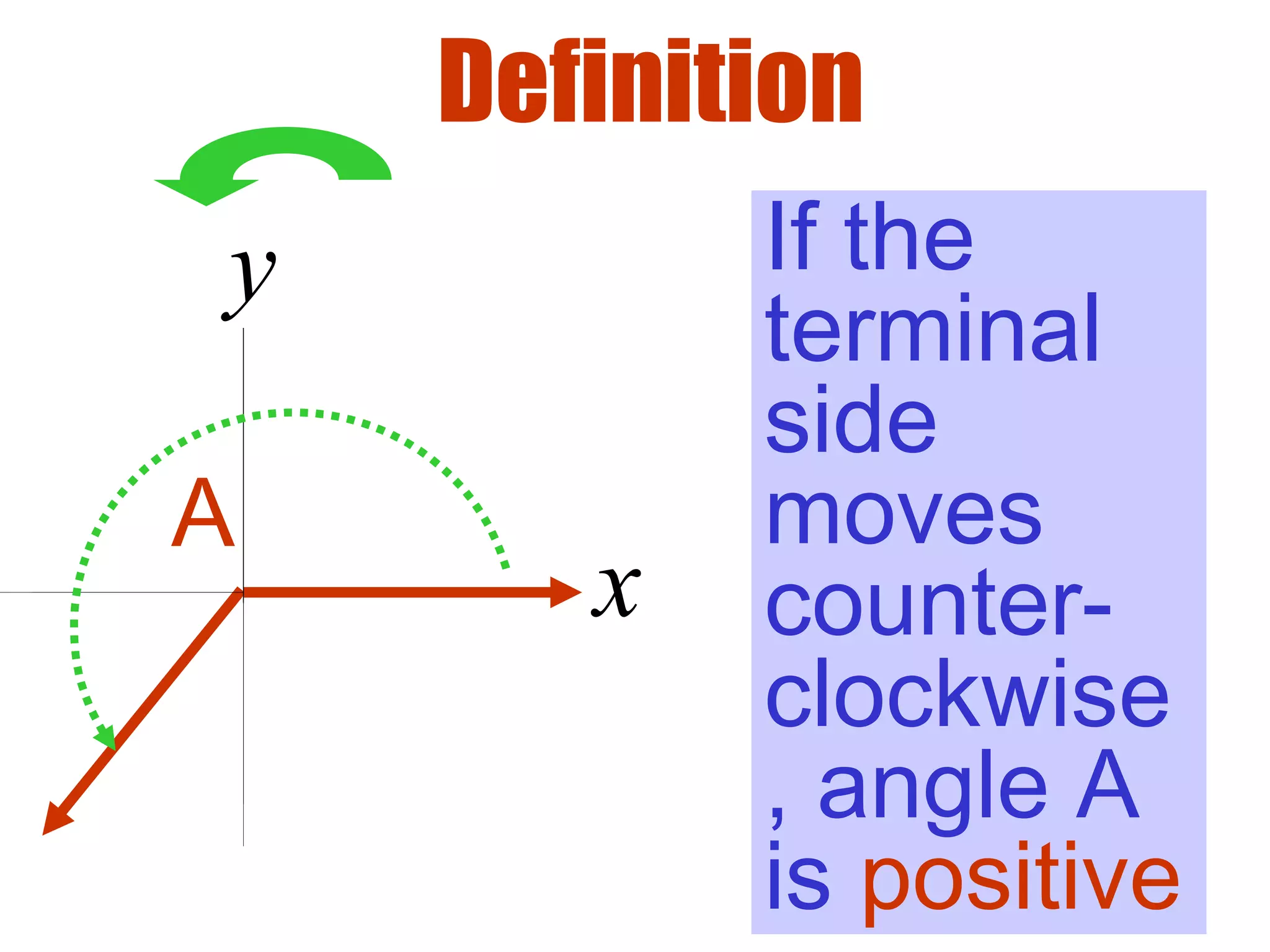
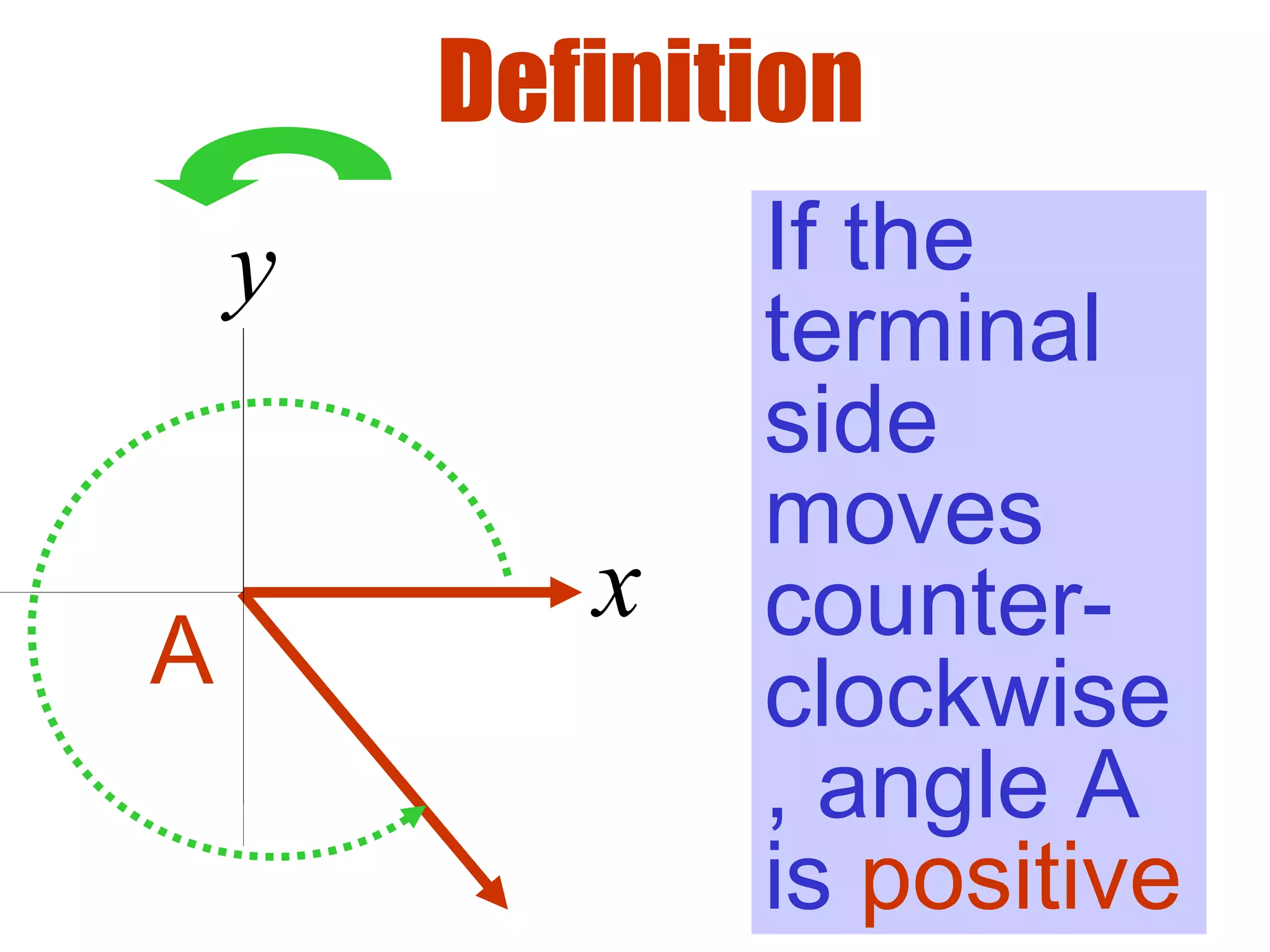
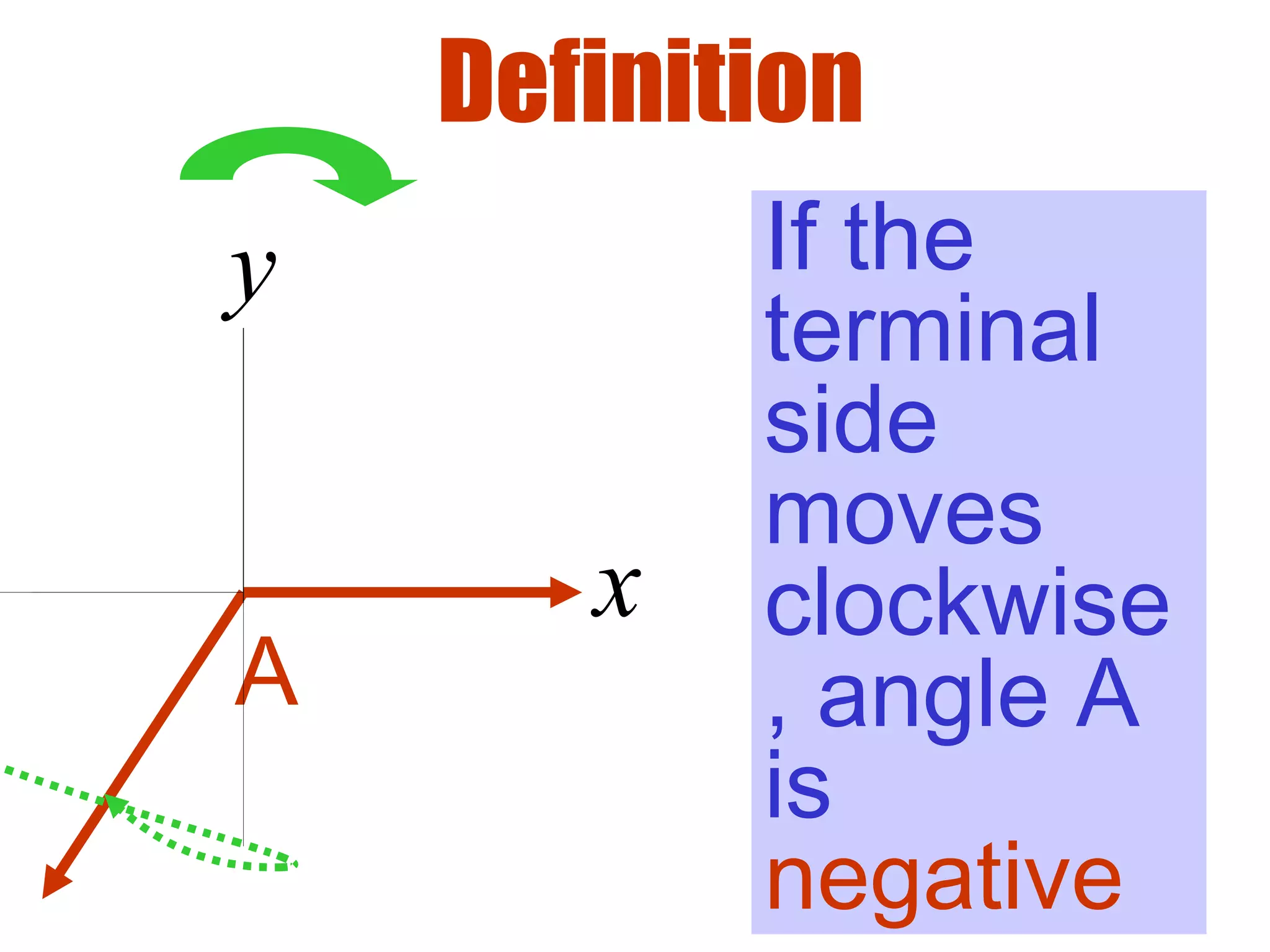
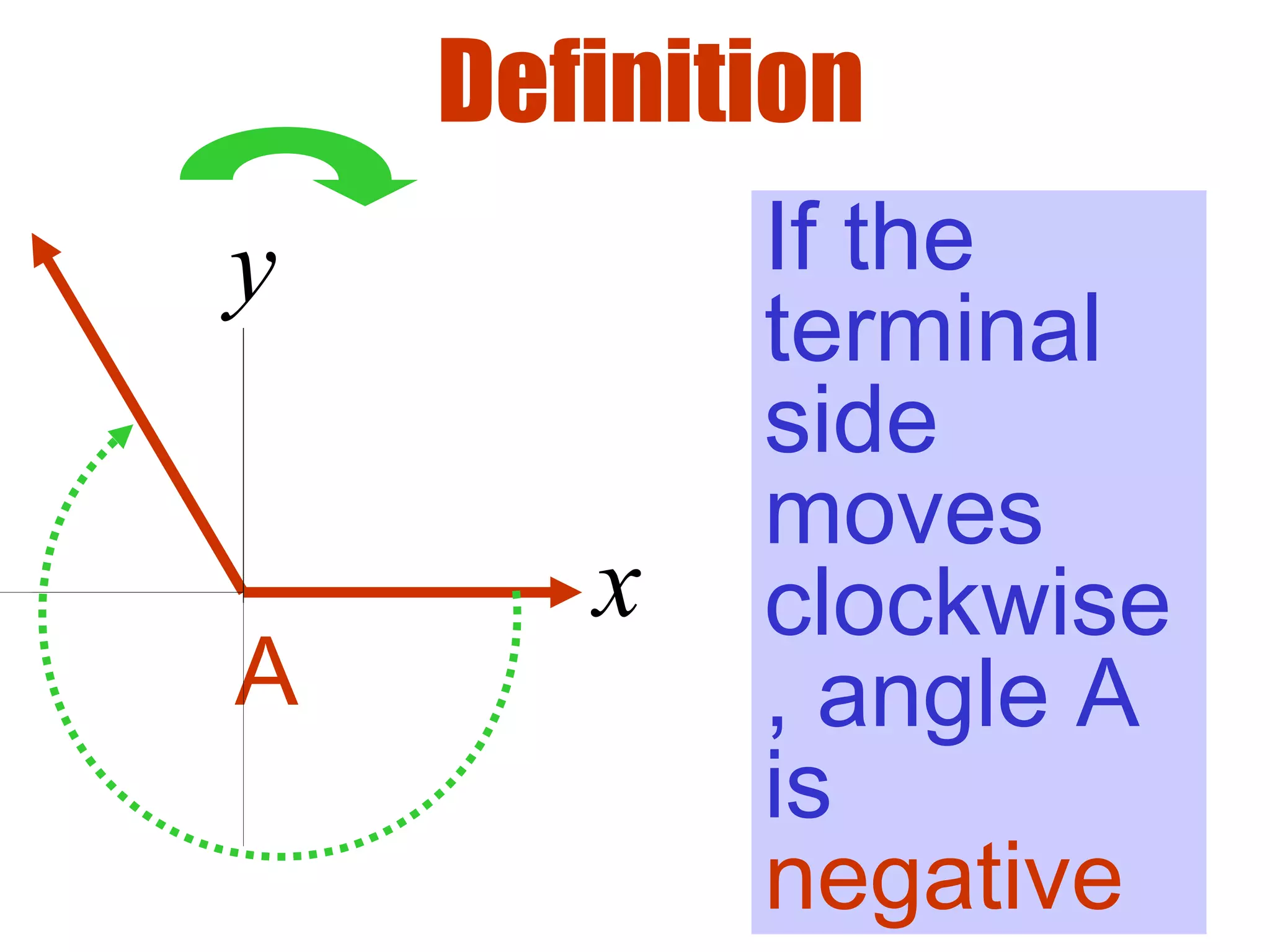
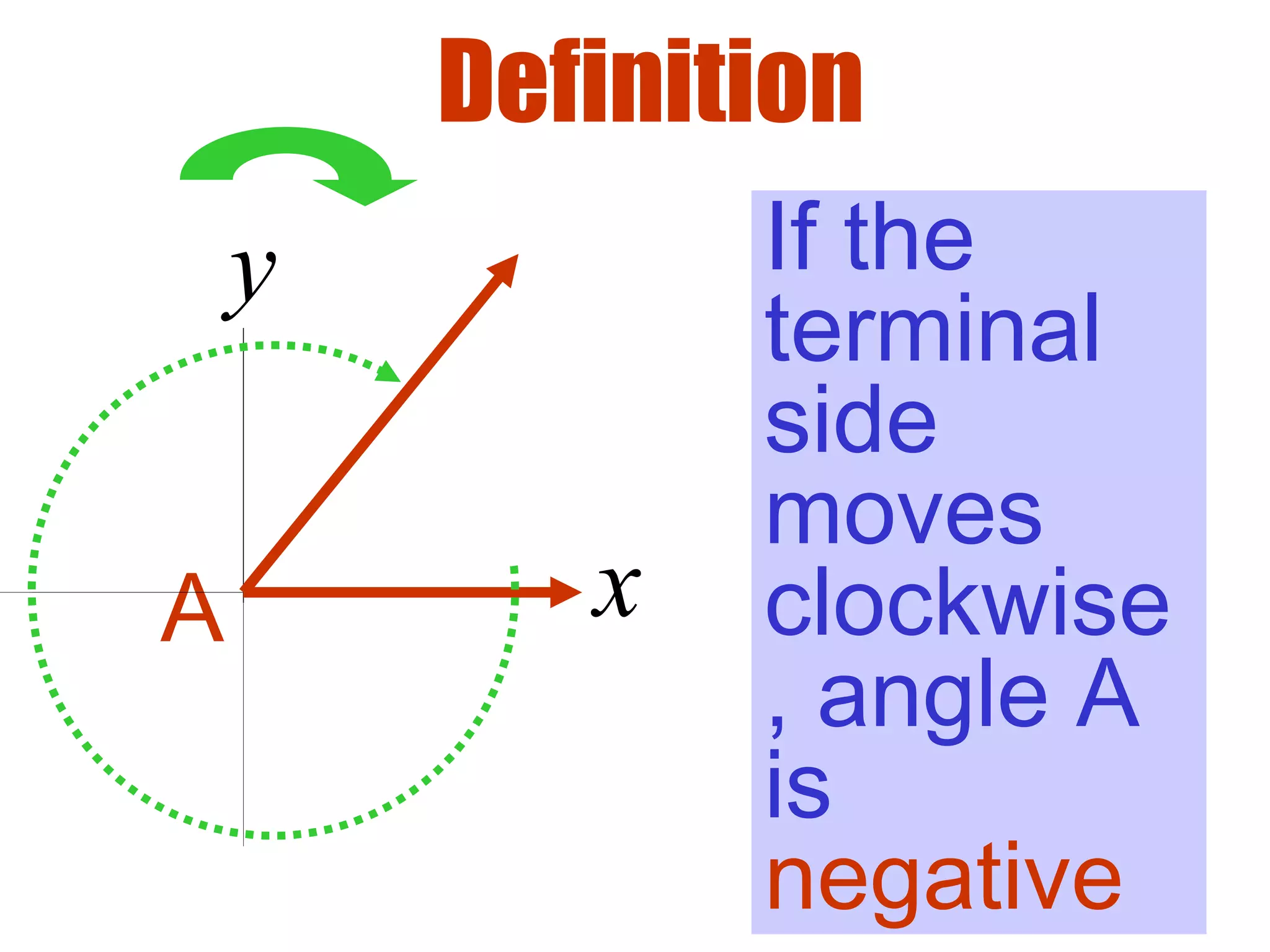
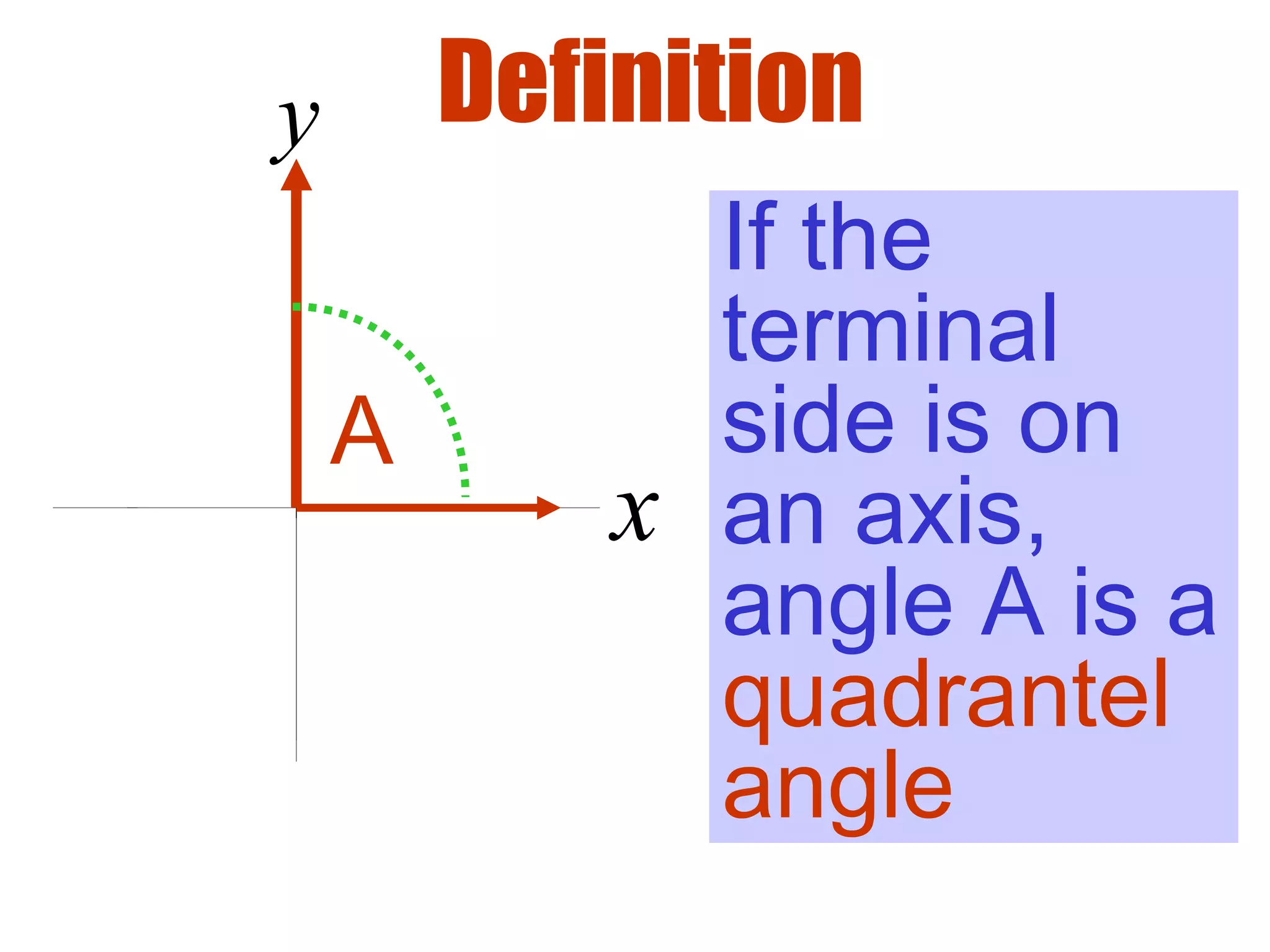
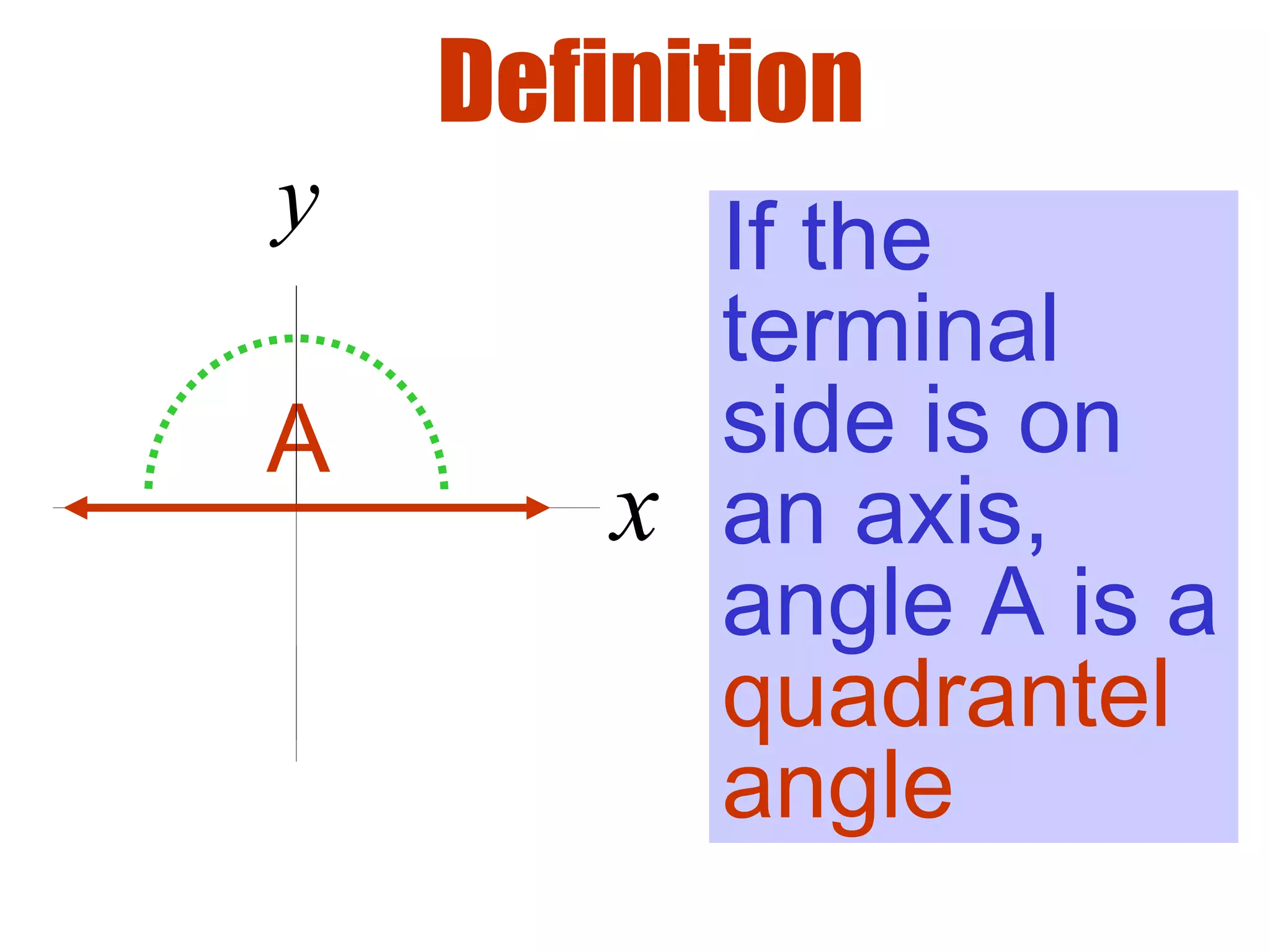
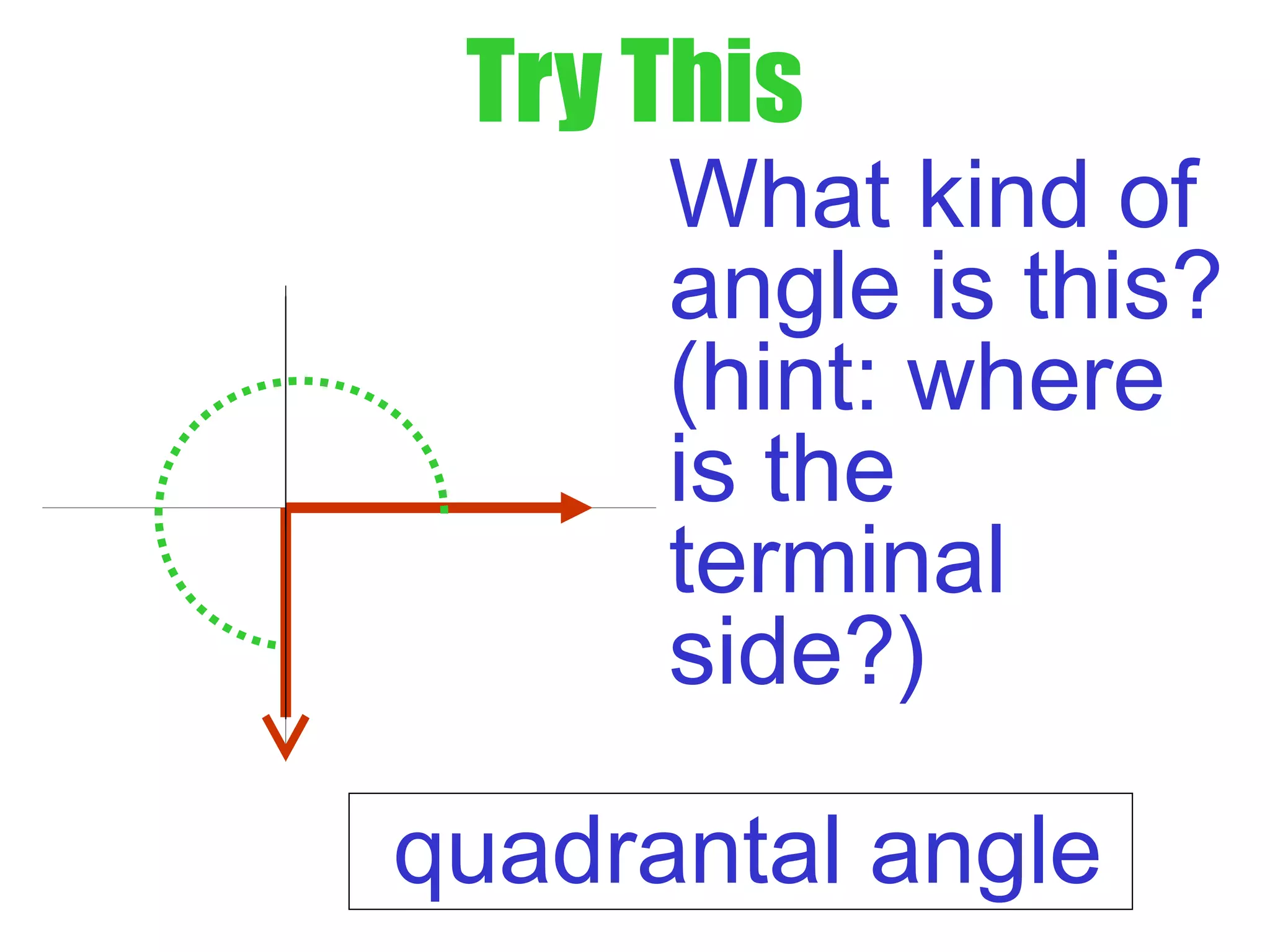
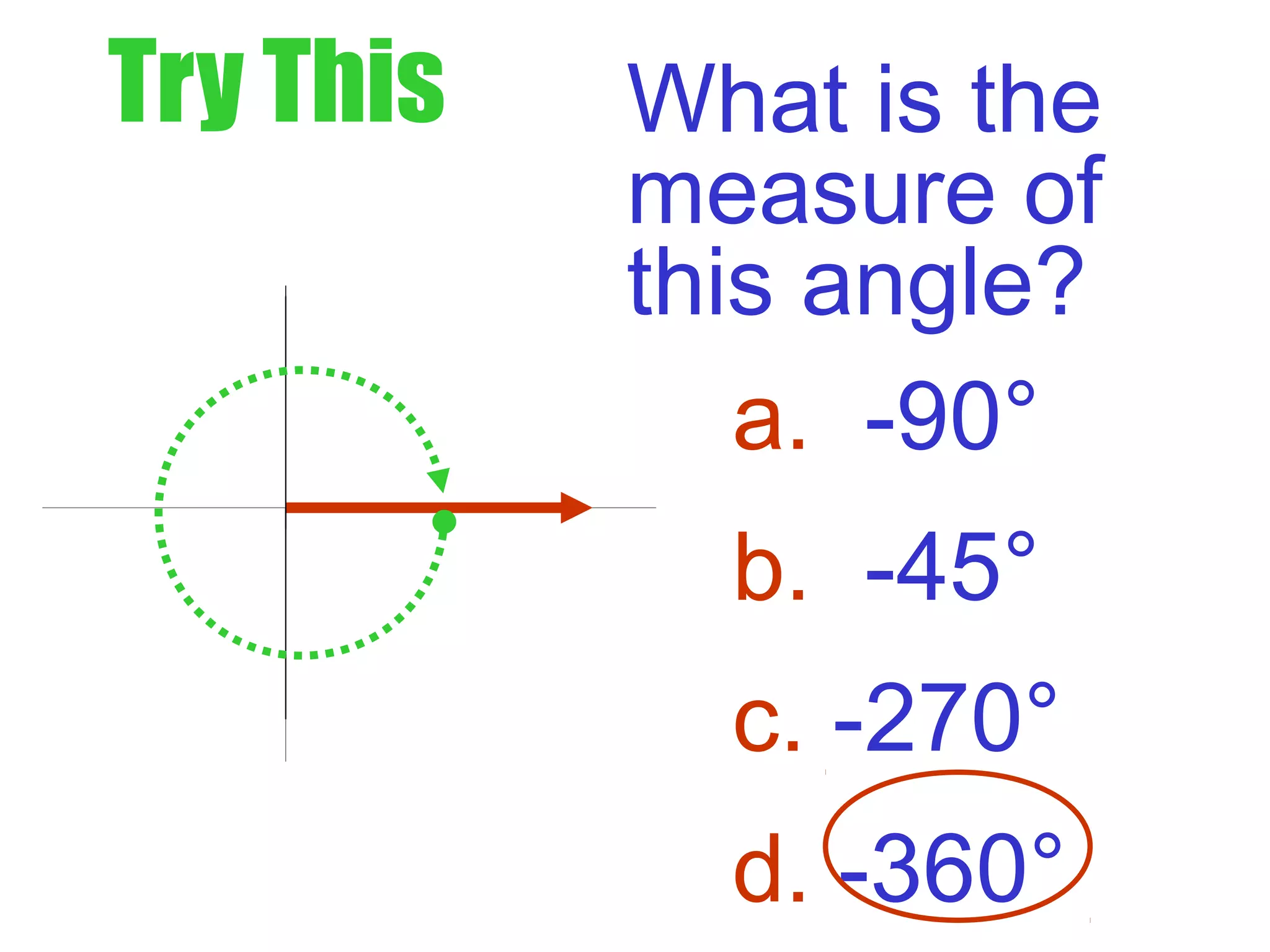
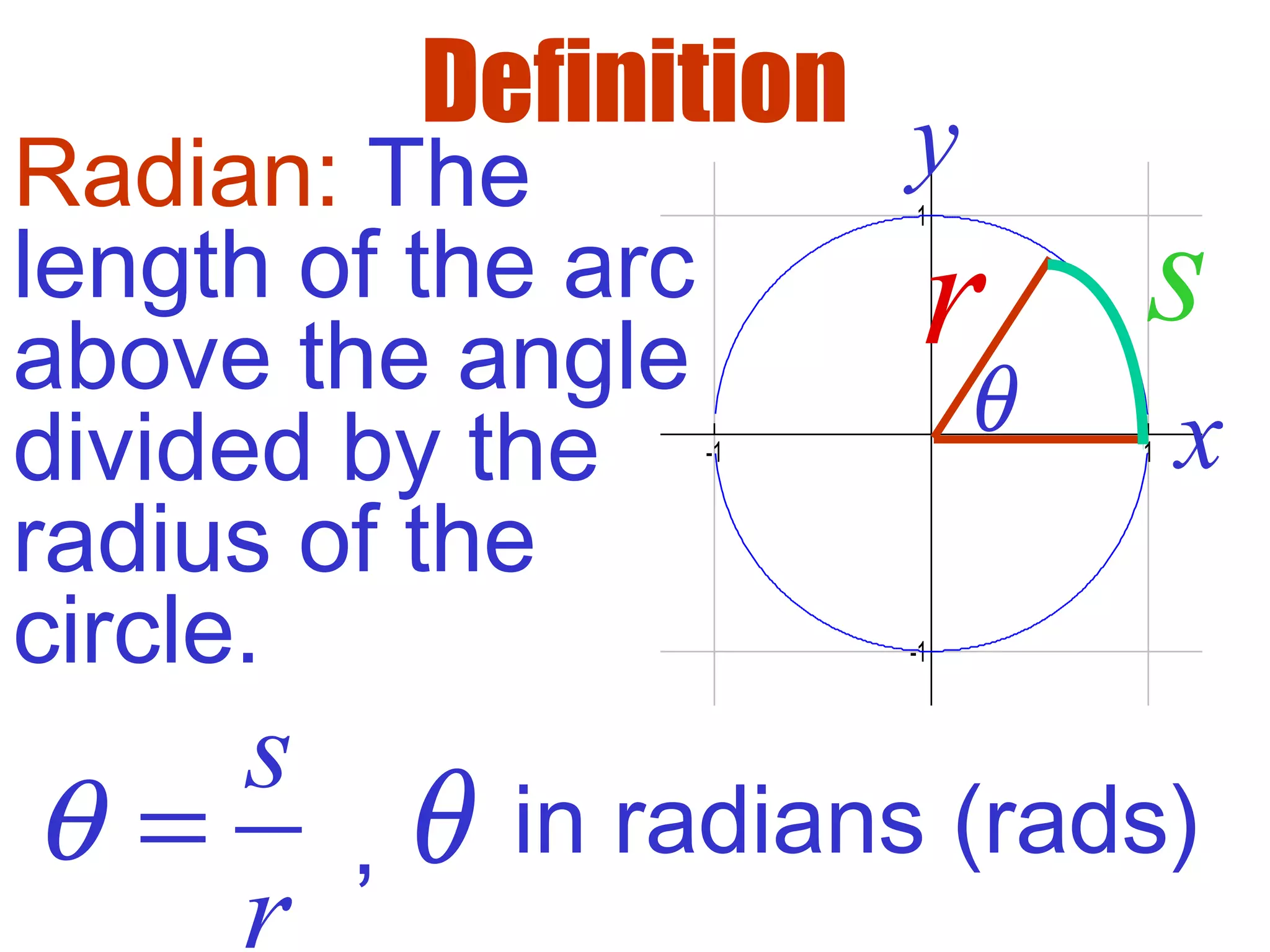
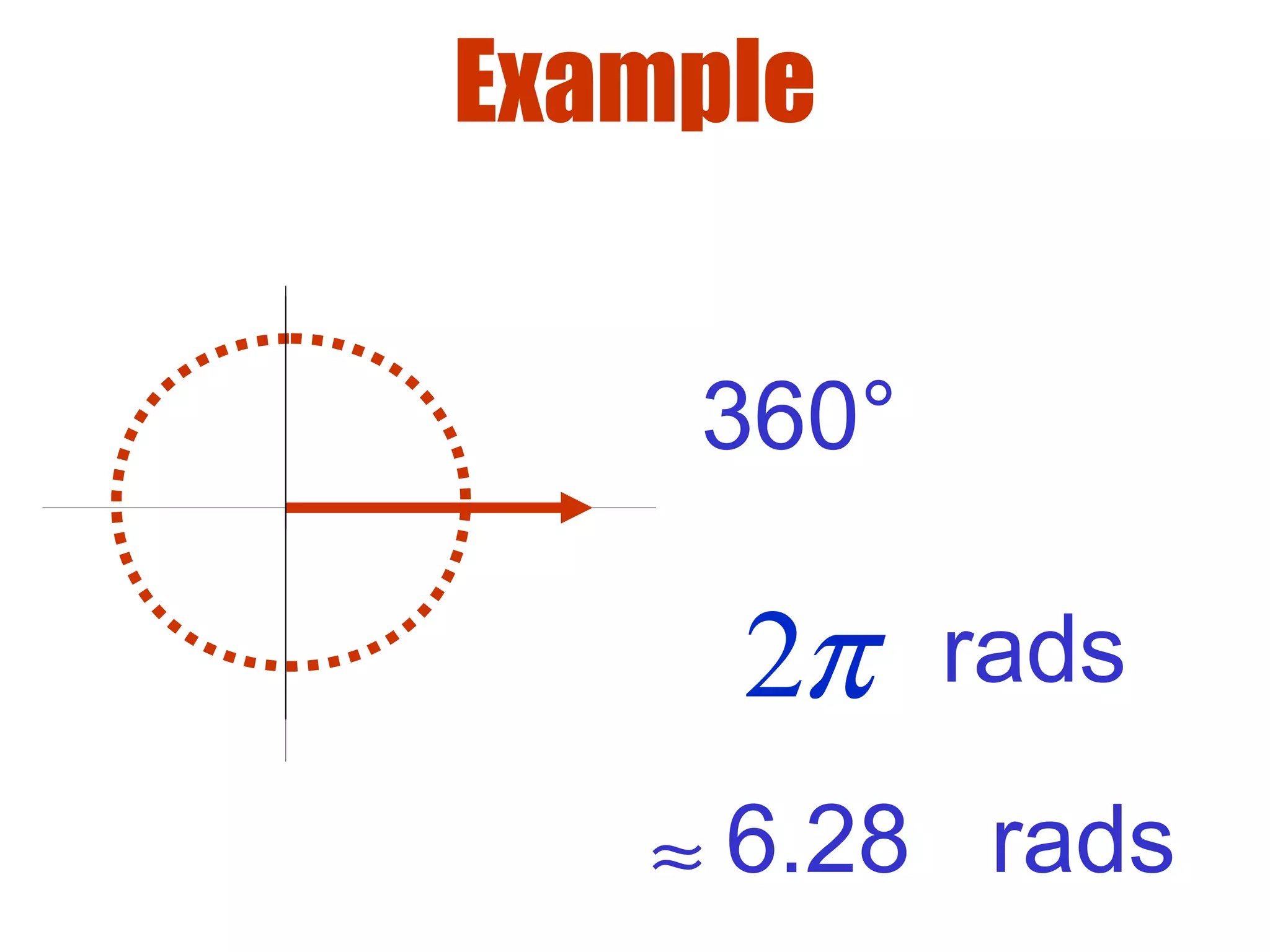
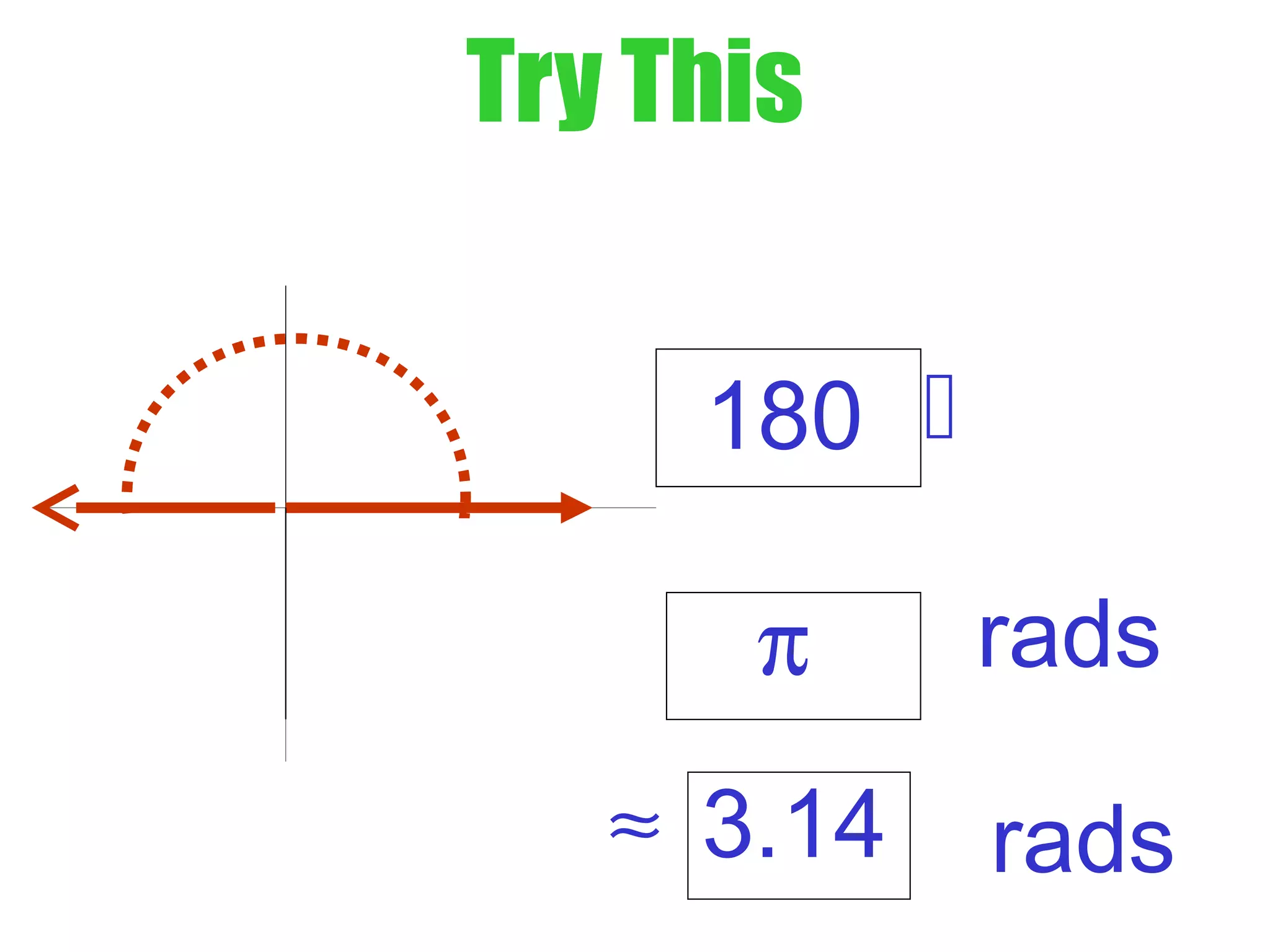
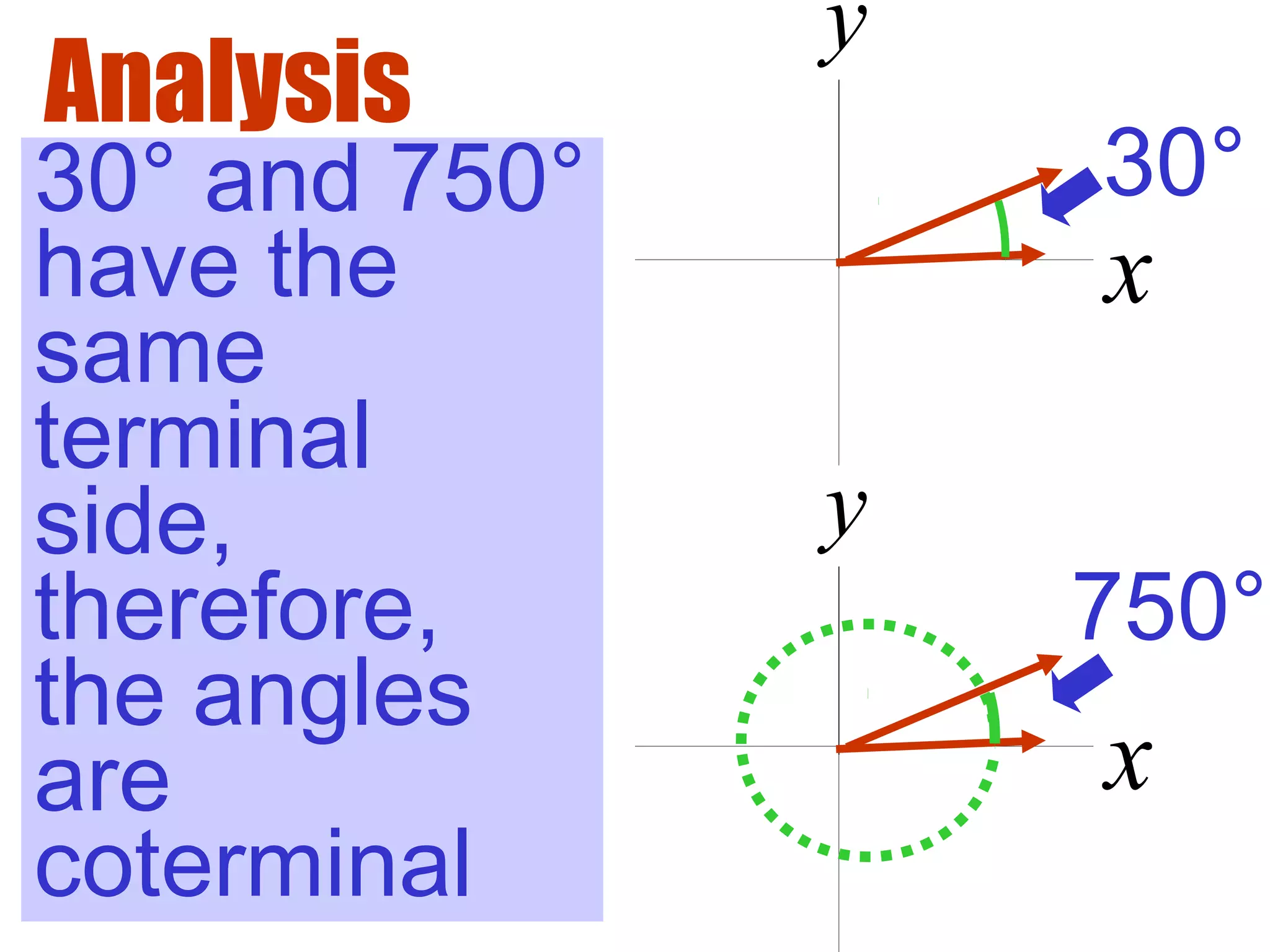
This document defines radians as a unit of measuring angles, where the radian measure of an angle is defined as the arc length of a unit circle subtended by the angle divided by the radius. It discusses converting between degree and radian measures, defines quadrantal angles in radians, and introduces the concept of coterminal angles which have the same terminal side.

1. 6-3: Angles and
Radian Measure
© 2007 Roy L. Gover (www.mrgover.com)
Learning Goals:
•Define radians as another
angle measure.
•Extend the definition of an
angle to include negative
angles and angles greater
than 180°

2. Definition
Initial Side
Terminal Side
Verte
x
Angle A
is in
standard
position
A
x
y

3. Definition
A
If the
terminal
side
moves
counter-
clockwise
, angle A
is positive
x
y

4. Definition
A
If the
terminal
side
moves
counter-
clockwise
, angle A
is positive
x
y

5. Definition
A
If the
terminal
side
moves
counter-
clockwise
, angle A
is positive
x
y

6. Definition
A
If the
terminal
side
moves
clockwise
, angle A
is
negative
x
y

7. Definition
A
If the
terminal
side
moves
clockwise
, angle A
is
negative
x
y

8. Definition
A
If the
terminal
side
moves
clockwise
, angle A
is
negative
x
y

9. Definition
A
If the
terminal
side
moves
clockwise
, angle A
is
negative
x
y

10. Definition
A
If the
terminal
side is on
an axis,
angle A is a
quadrantel
angle
x
y

11. Definition
A
If the
terminal
side is on
an axis,
angle A is a
quadrantel
angle
x
y

12. Definition
A
If the
terminal
side is on
an axis,
angle A is a
quadrantel
angle
x
y

13. Definition
A
If the
terminal
side is on
an axis,
angle A is a
quadrantel
angle
x
y
Is this an angle?

14. Try This
What kind of
angle is this?
(hint: where
is the
terminal
side?)
quadrantal angle

15. Try This What is the
measure of
this angle?
a. -90°
b. -45°
c. -270°
d. -360°

16. Try This What is the
measure of
this angle?
a. -90°
b. -45°
c. -270°
d. -360°

17. Try This What is the
measure of this
angle?
a. 0°
b. 45°
c. 90°
d. 120°
e. 180°

18. Try This What is the
measure of this
angle?
a. 0°
b. 45°
c. 90°
d. 120°
e. 180°

19. Try This What is the
measure of
this angle?
a. -90°
b. -45°
c. -270°
d. -360°

20. Try This What is the
measure of
this angle?
a. -90°
b. -45°
c. -270°
d. -360°

21. Try This
What is the
measure of
this
quadrantal
angle? x
y
0°

22. Try ThisIf a 143°
angle is in
standard
position,
determine
the quadrant
in which the
terminal side
lies.
x
y
2

23. Try ThisIf a 280°
angle is in
standard
position,
determine
the quadrant
in which the
terminal side
lies.
x
y
4

24. Important Idea
There are two units of
measure for angles:
•degrees: used in geometry
•radians: used in calculus
In Precal, we use degrees
and radians.

25. -1 1
-1
1
y
x
Radian: The
length of the arc
above the angle
divided by the
radius of the
circle.
Definition
sr
θ
s
r
θ = , θ in radians (rads)

26. -1 1
-1
1
y
x
Definition
s
θ
1
s
θ = , θ in radians (rads)
Unit Circle:
the circle with
radius of 1
unit
If r=1, =sθ
1

27. Definition
The radian measure of an
angle is the distance traveled
around the unit circle. Since
circumference of a circle is
2 r and r=1, the distance
around the unit circle is 2
π
π

28. Example
Find the degree
and radian
measure of the
angle in standard
position formed by
rotating the terminal side ½
of a circle in the positive
direction. Leave your radian
answer in terms of .π

29. Example
Find the degree
and radian
measure of the
angle in standard
position formed by
rotating the terminal side 5/6
of a circle in the negative
direction. Leave your radian
answer in terms of .π

30. Try This
Find the degree
and radian
measure of the
angle in standard
position formed by
rotating the terminal side 2/3
of a circle in the positive
direction. Leave your radian
answer in terms of .π

31. Solution
2
360 240
3
° = °g
2 4
2
3 3
π
π =g radians

32. Example
≈ rads
360°
rads
6.28
2π

33. Example
45 (degrees)
4
π
radians
≈ .785 radians

34. Example
90 (degrees)
2
π
radians
≈ 1.57 radians

35. Try This
≈ rads
180
radsπ
3.14

36. Try This
≈ rads
-180
rads-π
-3.14

37. Try This
≈ rads
270
rads
4.71
1 3
1 or
2 2
π
π
Do you see a pattern?

38. Important Idea
Radian measure allows the
expansion of trig functions
to model real-world
phenomena where
independent variables
represent distance or time
and not just an angle
measure in degrees.

39. Important Idea
If a circle contains 360° or 2π
radians, how many radians
are in 180°
• Use to change
rads to degrees
180°
π rads
• Use to change
degrees to rads
π rads
180°

40. Example
Change 30° to radian
measure in terms of π.

41. Try This
Change 120° to radian
measure in terms of π.
2
rads
3
π

42. Try This
Change 240° to radian
measure in terms of π.
4
rads
3
π

43. Example
Change radians to
degree measure.
3
4
π

44. Example
Change 2.356 radians to
degree measure.
(hint: radians are not
always stated in terms of
π.)

45. Try This
Change radians to
degree measure.
157.5°
7
8
π

46. Try This
Change -3.5 radians to
degree measure to the
nearest tenth.
-200.5°

47. Definition
0
2
π
π
3
2
π
The
quadrantal
angles in
radians
2π

48. Definition
0
2
π
π
3
2
π
The
quadrantal
angles in
radians
2π

49. Definition
0
2
π
π
3
2
π
The
quadrantal
angles in
radians
2π

50. Definition
0
2
π
π
The
quadrantal
angles in
radians
2π
The terminal side is on an
axis.

51. Definition
Coterminal Angles: Angles
that have the same terminal
side.
Important Idea
In precal, angles can be
larger than 360° or 2
radians.
π

52. Example
Find positive angles and
negative angles that are
coterminal with 30°.

53. Important Idea
To find coterminal angles,
simply add or subtract
either 360° or 2 radians
to the given angle or any
angle that is already
coterminal to the given
angle.
π

54. Analysis
30° and 390°
have the
same
terminal
side,
therefore,
the angles
are
coterminal
30°
x
y
x
y
390°

55. Analysis
30° and 750°
have the
same
terminal
side,
therefore,
the angles
are
coterminal
30°
x
y
x
y
750°

56. Analysis
30° and
1110° have
the same
terminal
side,
therefore,
the angles
are
coterminal
30°
x
y
x
y
1110°

57. Analysis
30° and
-330° have
the same
terminal
side,
therefore,
the angles
are
coterminal
30°
x
y
x
y
-330°

58. How many angles can you
find that are coterminal
with a 30° angle and how
do you find them?
With Mr.
Gover

59. Try This
Find 3 angles coterminal
with 60°
420°,780° and -300°

60. Try This
Find one positive angle and
two negative angle
coterminal with radians.3
2
π
and7
2
π
2
π− 5
2
π−,

61. Try This
Find two positive angle and
one negative angle
coterminal with radians.5
6
π−
and7
6
π 19
6
π 17
6
π−,

62. Lesson Close
In your own words and
without looking at your
notes, write a definition for:
•Coterminal angle
•Radian