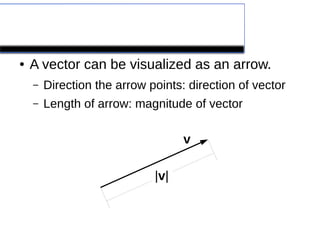
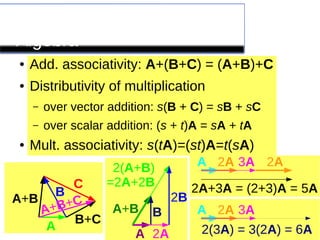
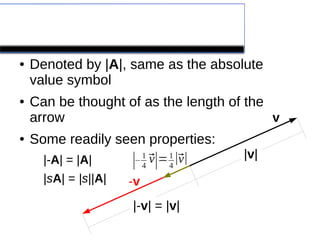
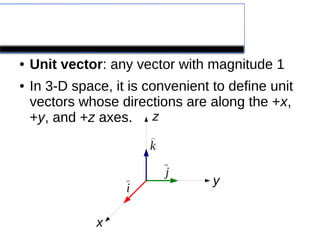
This lecture introduces the concepts of vectors and scalars, explaining their definitions, properties, and how to perform basic operations with them. It covers topics such as vector representation, addition, subtraction, and different algebraic manipulations in a coordinate system, emphasizing the differences between vectors and scalars. The lecture also includes examples and cautions against incorrect operations involving vectors and scalars.

1. Vectors and Scalars
Lecture 1

2. In this lecture, you will learn
● Physical interpretations and examples of
scalars and vectors
● Basic operations on scalars and vectors
● Properties of vector algebra
● How to represent vectors in abstract space
● How to carry out the basic operations
mathematically

3. What are vectors?
● Vector: “Quantity with magnitude and
direction”
– Velocity
– Force
– Acceleration
– Momentum
– Torque
v
F
a p
τ

4. What are scalars?
● Scalar: “Quantity with magnitude, but no
direction”
– Temperature
– Pressure
– Time
– Energy
– Mass
T
P
t
m
E

5. A joke
● What do you get when you cross a
disease-carrying mosquito with a mountain
climber?
?

6. A joke
● Undefined! You cannot cross a vector with
a scalar.

7. What was that for?
● Disease-carrying mosquito = vector
– From Latin vectus, to carry
● Vectors can be represented as arrows
– Can be thought of as conveyor belts that
“carry” objects from their tip to their tail

8. What was that for?
● Mountain climber = scaler
– Pronounced the same way as scalar
● Scalars are just real numbers (in physics,
usually with units)
– Their purpose is to scale vectors
⃗v
2⃗v
3⃗v

9. Vectors
● The precise definition of a vector is more
than just a quantity with magnitude and
direction...
...but you can think of vectors that way for
now.

10. Geometric Representation
● A vector can be visualized as an arrow.
– Direction the arrow points: direction of vector
– Length of arrow: magnitude of vector
v
|v|

11. Vector Addition
● Finding A + B is not as simple as 1 + 1 = 2.
● Copy B starting from the tip of A.
● OR copy A starting from the tip of B.
A
B
A
B
Resultant vectorResultant vector AA ++ BBResultant vectorResultant vector BB ++ AA
Notice that vector addition is commutative, i.e.,
A + B = B + A.
This is sometimes called the parallelogram law.

12. Scalar Multiplication
● This one's as simple as 1 × 2 = 2.
● The resultant vector has the same
direction, but its length (magnitude) is
scaled by the scalar.
● If the scalar is negative, then the resultant
points in the opposite direction.
⃗v
2⃗v
3⃗v
1
2
⃗v
−
1
2
⃗v
−2⃗v

13. The Zero Vector
● Represented by bold 0 or by a zero with an
arrow on top
● Additive identity of vectors: A + 0 = A.
● Scaling a vector by the scalar 0 gives the
zero vector, i.e., 0A = 0.
⃗0 ⃗A
⃗0+ ⃗A=⃗A
0 ⃗A=⃗0

14. The Negative of a Vector
● Same magnitude, pointing in the opposite
direction
● The negative of A is written as -A.
● Also known as additive inverse.
● Same as scaling by -1, i.e., (-1)A = -A.
● Additive inverse property: A + (-A) = 0.
⃗A
−⃗A
A-A
0

15. Vector Subtraction
● Just like with numbers, subtraction is
defined as the addition of the additive
inverse.
– That is, A – B = A + (-B).
⃗A
⃗B
−⃗B⃗A−⃗B

16. More Properties of Vector
Algebra
● Add. associativity: A+(B+C) = (A+B)+C
● Distributivity of multiplication
– over vector addition: s(B + C) = sB + sC
– over scalar addition: (s + t)A = sA + tA
● Mult. associativity: s(tA)=(st)A=t(sA)
A
B
C
A+B+CA+B
B+C
A 2A
B
2B
A+B
2(A+B)
=2A+2B
A 2A 3A 2A
2A+3A = (2+3)A = 5A
A 2A 3A
2(3A) = 3(2A) = 6A

17. Magnitude of a Vector
● Denoted by |A|, same as the absolute
value symbol
● Can be thought of as the length of the
arrow
● Some readily seen properties:
|-A| = |A|
|sA| = |s||A|
v
|v|
|-v| = |v|
-v
∣−
1
4
⃗v∣=1
4
∣⃗v∣

18. Vectors in a Coordinate
System
● Drawn starting from the origin
● Expressed in terms of their components
<2, 3>
<-1, -6>
x-comp = 2
y-comp = 3
x-comp = -1
y-comp = -6
x
y

19. Unit Vectors
● Unit vector: any vector with magnitude 1
● In 3-D space, it is convenient to define unit
vectors whose directions are along the +x,
+y, and +z axes.
x
y
z
̂i
̂j
̂k

20. Algebraic Representation of
Vectors
● The standard unit vectors i, j, and k form
what is called an orthonormal basis of 3-D
space, because any 3-D vector can be
expressed uniquely in terms of i, j, and k.
● A 3-D vector denoted by <x, y, z> can be
written as xi + yj + zk.
x
y
z
r = xi + yj + zk
xy
z

21. Algebraic Addition of
Vectors
● Just add the vectors component by
component.
A = 2i + 3j
x
y
B = 3i – 7j
A + B = (2+3)i + (3–7)j
A + B = 5i – 4j
x-components
y-components

22. Algebraic Multiplication of a
Vector by a Scalar
● Multiply each component by the scalar.
x
A = -2i + j
3A = -6i + 3j

23. Example 1
● If A = 3i – 4j + k, B = -2i + 5j + 7k, and
C = 2i + 4k, solve for 7A + 4B – 8C.
● Solution:
7(A = 3i – 4j + k)
4(B = -2i + 5j + 7k)
-8(C = 2i + 4k)
7A = 21i – 28j + 7k
4B = -8i + 20j + 28k
-8C = -16i – 32k
7A + 4B – 8C = -3i – 8j + 3k

24. Example 2
● If P = 2j + 7k and R = 3i – 4j – 2k, find Q
such that 4P + 3Q = R.
● Solution:
Start with 4P + 3Q = R. Isolate Q.
Q = (1/3)R – (4/3)P
Q = (1/3)(3i – 4j – 2k) – (4/3)(2j + 7k)
Q = i – (4/3)j – (2/3)k – (8/3)j – (28/3)k
Q = i – 4j – 10k

25. A few words of caution
● You cannot add a scalar and a vector.
For example, 4 + 4j is undefined.
● You cannot multiply two vectors.
For example, (4i – j)(3j + k) is undefined.
– However, in the next lecture, you'll learn about
two different kinds of “product” operations you
can do on vectors: the dot product and the
cross product.

26. Problems
1.If A = 3j + 6k and B = -2i – 2j + 5k, find:
(a)2A – 3B
(b)-4A + B
2.If C = 2i + 5j and D = -4i + j, find E such
that C – 2E = 3D.
3.Given A = 2j + 3k, B = 3i – 6j + 4k,
C = 26i + 9j – 6k, and r = aA + bB + cC, find
a, b, and c if
(a) r = 18i – 38j + 21k
(b) r = -32i + 19j + 22k