This document discusses solving exponential and logarithmic equations using properties of functions and logarithms. It provides 7 examples of solving different types of equations: 1) Powers of the same base by creating a common base 2) Powers of different bases by taking logarithms of both sides 3) Powers of different bases by taking logarithms and setting them equal 4) Using substitution to eliminate negative exponents 5) Applying exponential decay to radiocarbon dating 6) Using compound interest formula to solve for time 7) Using population growth formula to solve for time of reaching a population size It also provides 2 examples of solving logarithmic equations: 8) Equating logarithmic terms and constants by taking exponents 9) Equ

1. Solving
Exponential and
Logarithmic
Equations

2. • By the definition of a function, if u = v and f is
a function, then f(u) = f(v) [remember each input of a
function has one and only one output!]
• So, let’s say we have a function f(x) = b?,
then if u = v then bu = bv for all real #s b>0
• Likewise, if we have a function f(x) = logb?,
if u = v then logbu = logbv for all real #s b>0
• And because exponential and logarithmic
functions are one-to-one (i.e. their inverses
are also functions), then the converse is true:
– If bu = bv then u = v
– If logbu = logbv then u = v

3. Now, let’s use these
statements, (and all the other
properties for exponents and logarithms),
to solve:
Exponential and Logarithmic
equations

4. Example 1: Powers of the Same Base
Solve 8x = 2x+1
Can you create a common base?
(23)x = 2x+1
23x = 2x+1
3x = x+1
2x = 1
x = ½
Graph Y=8x and Y=2x+1 to confirm

5. Example 2: Powers of Different Bases
Solve 5x = 2
ln5x = ln2
xln5 = ln2
x = ln2/ln5
x = 0.6931/1.6094
x = 0.4307
Graph Y=5x and Y=2 to confirm

6. Example 3: Powers of Different Bases
Solve 24x-1 = 31-x
ln(24x-1) = ln(31-x)
(4x-1)ln2 = (1-x)ln3
4xln2 – ln2 = ln3 – xln3
4xln2 + xln3 = ln3 +ln2
x(4ln2 + ln3) = ln3 +ln2
x = (ln3 + ln2)/(4ln2 + ln3)
x = 0.4628
Graph Y=24x-1 and Y= 31-x to confirm

7. Example 4: Using Substitution
Solve ex – e-x= 4
Multiply each side by ex to eliminate negative exponents
ex(ex – e-x ) = ex(4)
exex – exe-x = ex(4)
e2x - 1 = 4ex
e2x - 4ex - 1 = 0
Let u = ex and substitute
u2 -4u -1 = 0

9. Now, let’s do the same
thing by solving some real
world applications of
exponential equations

10. Example 5: Radiocarbon Dating
The half life of carbon-14 is 5730
years. The skeleton of a mastodon has
lost 58% of its original carbon-14.
When did the mastodon die?
What is the half-life formula?
f(x) = P(0.5)x/h (P is initial amount; h is half-life, x is # years)
So, f(x) = P(0.5)x/5730
.42P = P(0.5)x/5730

11. 0.42P = P(0.5)x/5730
0.42 = (0.5)x/5730
ln0.42 = ln(0.5)x/5730
ln0.42 = (x/5730)ln0.5
x = (5730)(ln0.42)/ln0.5
x = 7171.3171
Graph Y=0.42 and Y=(0.5)x/5730 to confirm

12. Example 6: Compound Interest
If $3000 is to be invested at 8% per
year, compounded quarterly, in how
many years will the investment be
worth $10,680?
What is the compound interest formula?
A = P(1+r)t (A is amount after t periods; P is the principal; r is
interest rate)
So, 10,680 = 3000(1+.08/4)4t
10,680 = 3000(1.02)4t

13. 10,680 = 3000(1.02)4t
3.56 = (1.02)4t
ln3.56 = ln(1.02)4t
ln3.56 = (4t)ln(1.02)
4t = ln3.56/ln1.02
t = (ln3.56/ln1.02)/4
t = 16.03 years
Graph Y=10680 and Y=3000(1.02)t/4 to confirm

14. Example 7: Population Growth
The population of a certain type of bacteria grows by the
function S(t) = Pert, where P is the initial population and r is a
continuous growth rate. If a biologist has a culture that contains
1000 bacteria, and 7 hours later there are 5000 bacteria:
a. Write the function for this population
b. When will the population reach 1 billion?
a. What does the equation look like when evaluated at t = 7, i.e. when S(7) =
5000?
5000 = 1000er(7)
5 = e7r
ln5 = lne7r
ln5 = 7rlne (lne = 1)
ln5 = 7r
r = 0.2299
So the function for this population is S(t) = 1000e0.2299t

15. b. When will the population reach 1
billion?
b. S(t) = 1000e0.2299t
1000e0.2299t = 1,000,000,000
e0.2299t = 1,000,000
lne0.2299t = ln1,000,000
0.2299t lne = ln1,000,000 (lne =1)
t = ln1,000,000/0.2299
t = 60.0936 hours
Graph Y=1000e0.2299t and Y=1 billion to confirm

16. Ex 8: Inhibited Population Growth
A population of fish in a lake at time t months is given by:
F(t)=20,000/(1+24e-t/4)
How long will it take for the population to reach 15,000?
15000 = 20000/(1+24e-t/4)
15000(1+24e-t/4) = 20000
1+24e-t/4 = 20000/15000
24e-t/4 = 4/3 - 1
e-t/4 = (1/3)(1/24)
lne-t/4 = ln (1/72)
(-t/4)lne = ln1 - ln72
-t/4 = 0 – ln72 (lne=1, ln1=0)
t = 4ln72 = 17.1067
Graph Y=15000 and Y=20000/(1+24e-t/4) to confirm

17. Now, let’s solve some
logarithmic equations
using the properties of
one-to-one functions
to help

19. Example 10: Equations with Logarithmic
and Constant Terms
Solve ln(x – 3) = 5 - ln(x – 3)
First put all log terms on one side of equal sign &
constants on the other
ln(x – 3)+ ln(x – 3)= 5
2ln(x - 3) = 5
ln(x -3) = 5/2
e ln(x -3) = e5/2
x -3 = e5/2
x = e5/2 +3 = 15.1825
Graph Y= ln(x-3) and Y= 5 – ln(x-3) to confirm

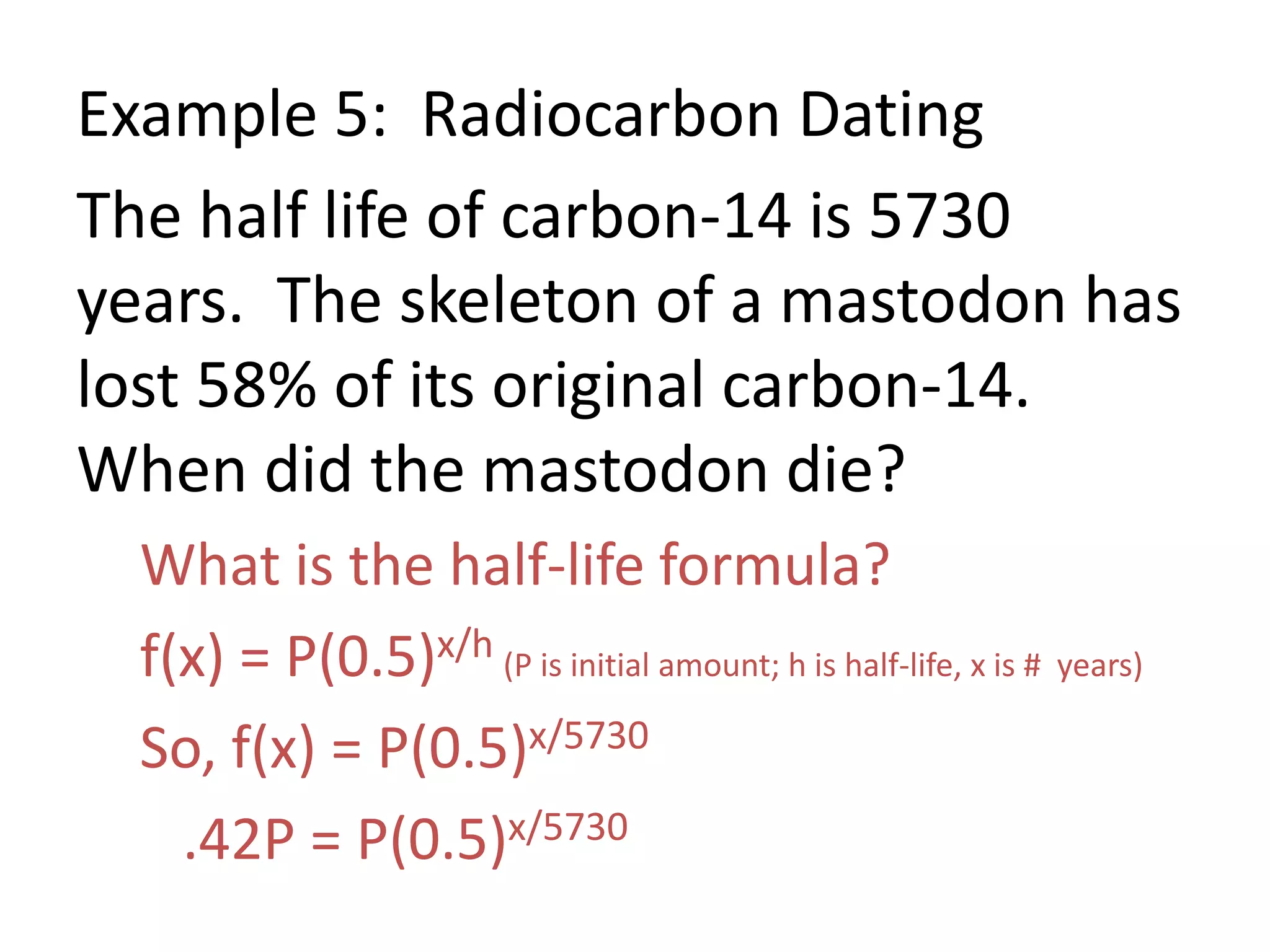
20. Example 11: Equations with Logarithmic
and Constant Terms
Solve log(x – 16) = 2 - log(x – 1)
log(x – 16)+ log(x – 1) = 2
log[(x-16)(x-1)] = 2
log(x2 -17x +16) = 2
10 log(x2 -17x +16) = 102
x2 -17x +16 = 100
x2 -17x – 84 = 0
(x +4)(x – 21) = 0
x = -4 and 21, but log(x-16) and log(x-1) are not
defined for x = -4, so only x = 21 is valid
Graph Y= log(x-16) and Y= 2 – log(x-1) to confirm