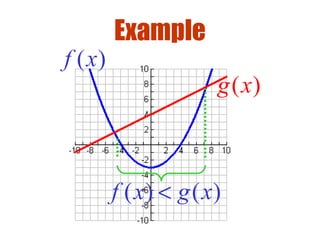
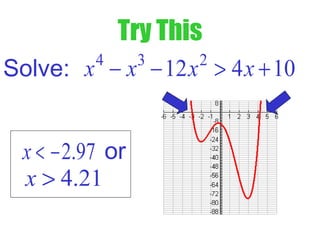
This document provides an overview of solving inequalities, including: 1) The principles for solving inequalities are similar to equations but the direction of the inequality changes when multiplying or dividing by a negative number. 2) Interval notation is used to represent the solutions of inequalities on the number line. 3) To solve inequalities, determine the zeros of the function and where the graph is above or below the x-axis to identify the intervals of solutions.

1. 2-5: Inequalities
© 2007 Roy L. Gover (www.mrgover.com)
Learning Goals:
•Use interval notation
•Solve linear and compound
linear inequalities
•Find exact solutions of
quadratic and factorable
inequalities

2. Important Idea
In previous sections, we
have been solving equalities,
or equations. Now we are
going to solve inequalities.
The methods of solving
equalities and inequalities
are similar but there are
important differences.

3. Definition
The statement c<d means
that c is to the left of d on
the number line.
d
c

4. Definition
The statement c>d means
that c is to the right of d on
the number line.
d
c

5. Important Idea
The statement c<d and d>c
mean the same thing.

6. Definition
The statement b<c<d, called
a compound inequality
means:
b<c and simultaneouslyc<d

7. Definition
( ),c d c x d⇔ < <
( ],c d c x d⇔ < ≤
Interval Notation:Let x,c & d
be real numbers with c<d:
[ ],c d c x d⇔ ≤ ≤
[ ),c d c x d⇔ ≤ <

8. Example
Write the following using
interval notation:
2 5x< <
2 5x≤ <
3 8x≤ ≤

9. Try This
Write the following using
interval notation:
3 8x< ≤
( ]3,8

10. Try This
What do you think this
means?
[ )19,∞
( ),0−∞

11. Important Idea
Principles for solving
inequalities:
1. Add or subtract the
same number on both
sides of the inequality.

12. Important Idea
Principles for solving
inequalities:
2. Multiply or divide both
sides of the inequality by
the same positive number.

13. Important Idea
Principles for solving
inequalities:
3. Multiply or divide both
sides of the inequality by
the same negative number
and reverse the direction of
the inequality.

14. Example
2 3 5 2 11x x≤ + < +
Solve. Write your answer
using interval notation.

15. Try This
5 2 1 7x x− ≤ − ≤ +
[ ]2,8−
Solve. Write your answer
using interval notation.

16. Example
4 3 5 18x< − <
Solve. Write your answer
using interval notation.
Graph your answer on a
number line.

17. Try This
Solve. Write your answer
using interval notation.
Graph your answer on a
number line.
2
,2
3
 
− ÷
 
2 4 3 6x− < − <

18. Important Idea
The solutions of the form
( ) ( )f x g x< consist of
intervals on the x axis where
the graph of f is below the
graph of g.

19. Example
( )f x
( )g x
( ) ( )f x g x<

20. Important Idea
The graph of ( ) ( )y f x g x= −
lies above the x axis when
( ) ( )f x g x o− > and below
the x axis when
( ) ( )f x g x o− <

21. Example
Solve:
4 3 2
10 21 40 80x x x x+ + > +
Hint: Rewrite the
inequality.

22. Try This
Solve: 4 3 2
12 4 10x x x x− − > +
2.97x < − or
4.21x >

23. Important Idea
Solving an inequality
depends only on knowing
the zeros of the function
and where the graph is
above or below the x-
axis. The zeros are where
the function touches the x
axis.

24. Example
Find the exact solutions:
2
6 0x x− − ≤

25. Example
Find the exact solutions:
2
2 3 4 0x x+ − ≤
Confirm with your calculator

26. Try This
2
3 2 0x x+ − ≤
Find the exact solutions:
3 17 3 17
,
2 2
 − − − +
 
 

27. Example
Find the exact solutions:
Confirm with your calculator
6
( 5)( 2) ( 8) 0x x x+ − − ≤

28. Important Idea
Steps for solving inequalities:
1. Write the inequality in one
of these forms:
( ) 0f x > ( ) 0f x ≥
( ) 0f x < ( ) 0f x ≤

29. Important Idea
Steps for solving inequalities:
2. Determine the zeros of f,
exactly if possible,
approximately otherwise.

30. Important Idea
Steps for solving inequalities:
3. Determine the intervals on
the x axis where the graph is
above or below the x axis.

31. Example
A store has determined the
cost C of ordering and storing
x laser printers.
300,000
2C x
x
= +
The delivery truck can bring
at most 450 printers. How
many should be ordered to
keep the cost below $1600?

32. Lesson Close
Tell me everything you
know about solving
inequalities.