This document provides instruction on solving trigonometric equations algebraically. It begins by presenting examples of solving equations of the form sin(x) + cos(x) = 0 and 2cos(x) = 3 using algebraic methods like factoring. It then discusses the concept of principal values and using inverse trig functions when exact solutions cannot be obtained. Various trigonometric identities are presented that can be used to rewrite equations in terms of a single trig function before solving. Students are guided through additional examples and practice problems involving trig equations with solutions checked.

1. 8.3: Algebraic Solutions of
Trigonometric Equations
© 2008 Roy L. Gover(www.mrgover.com)
Learning Goals:
•Solve Trigonometric
equations using Algebraic
methods.

2. Try This
Using your knowledge of
Algebra and factoring, solve
the equation:
2
0x x+ =
0, 1x x= = −
Check your answer.

3. Example
Solve the equation and
check the solution:
2
sin sin 0x x+ =

4. Important Idea
Always check your
solution(s) in the original
equation.

5. Try This
Using your knowledge of
Algebra, solve the equation:
2 3 9x + =
3x =
Check your answer.

6. Example
Solve the equation and
check the solution:
2cos 1 3θ + =

7. Important Idea
Similar methods are
used to solve algebraic
and trigonometric
equations.

8. Example
Solve for all values:
…there are an infinite
number of solutions.
2cos 3x =

9. Definition
Principal Values in Degrees:
& tan x: 90 90x− ° ≤ ≤ °
cos x: 0 180x° ≤ ≤ °
Principal values
insure unique
sin x

10. Definition
Principal Values in
Radians:
sin x & tan x:
2 2
x
π π
− ≤ ≤ +
cos x: 0 x π≤ ≤
Principal values
insure unique

11. Try This
Solve for the principal value:
2cos 1 0x − =
60x = ° or
3
π

12. Try This
Solve for the principal
value in degrees:
30x = − °
What is the
answer in
rads? 6
x
π
= −
2sin 1 0x + =

13. Try This
Solve for the principal
value in radians:
3sin 1x =
.340x =

14. Important Idea
When you
cannot get
exact values
for solutions,
you must use
the inverse trig
functions on
your calculator.
1
sin x−
1
cos x−
1
tan x−
•
•
•

15. Try This
Solve for the principal
value in degrees:
8cos 5 0θ − =
51.318x = °

16. Example
Solve for all values in
degrees:
8cos 5 0θ − =

17. Try This
Solve: 2sin 5 0x − =
???????

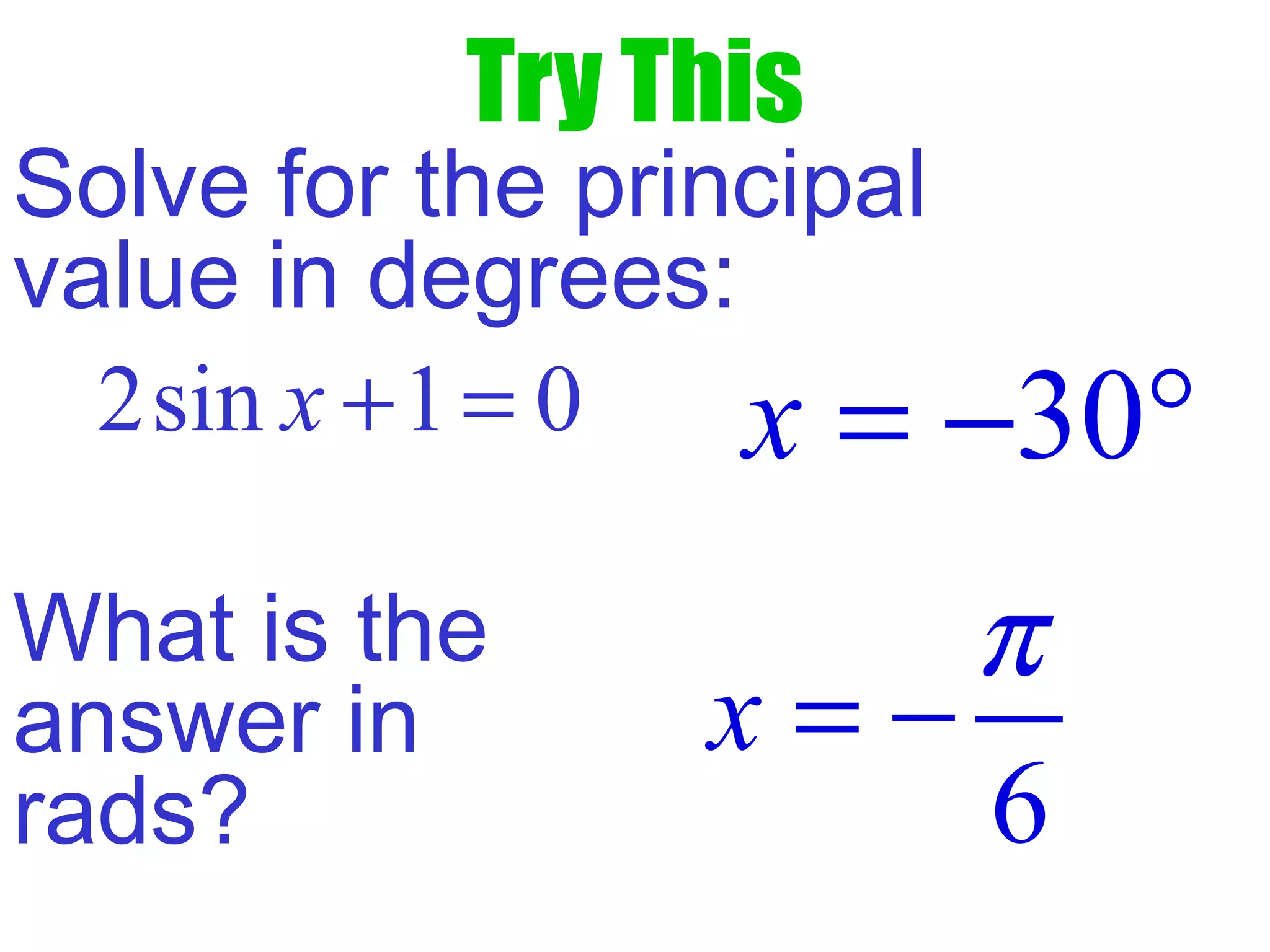
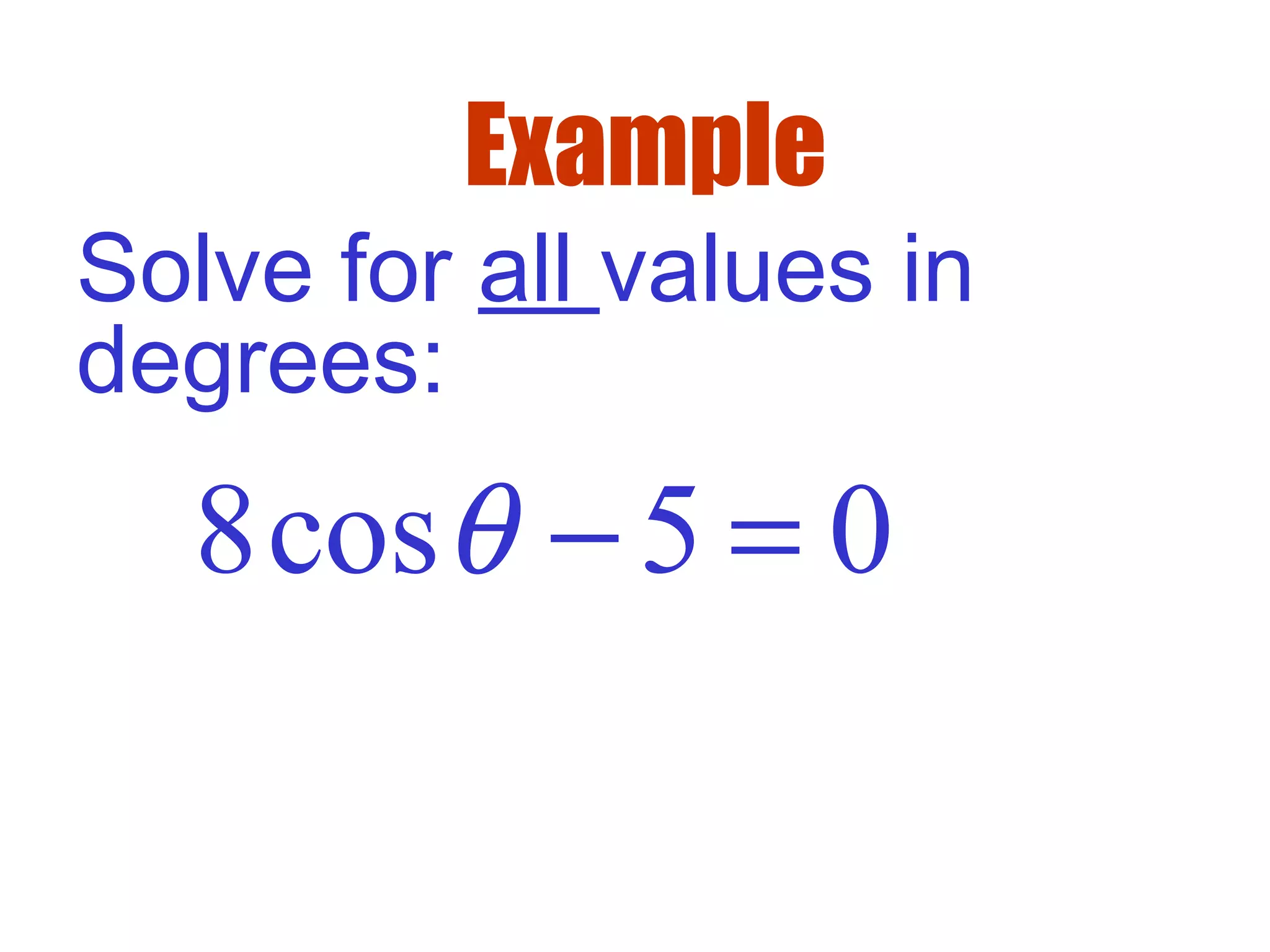
18. Important Idea
The value of sin x and cos x
can never be greater than 1
or less than -1
Range:
sin x : [-1,1]
cos x : [-1,1]

19. Try This
Using your knowledge of
Algebra and factoring, solve
the equation:
2
2 0x x− − =
1, 2x x= − =
Check your answer.

20. Example
Solve the equation and
check the solution:
2
sin sin 2 0x x− − =

21. Try This
Solve the equation and
check the solution:
2
cos cos 2 0x x+ − =
0x =
Are there other solutions?

22. Example
Find all solutions of
2
3sin sin 2 0x x− − =

23. Try This
Solve for the principal
values in radians:
2
2sin sin 1 0x x+ − =
6
x
π
= or
2
π
−
Why is not an answer?
3
2
π

24. Example
Find all solutions in
radians:
2
tan cos tanx x x=

25. Try This
Find the principal value
solutions in degrees:
2
cos sin cosx x x=
90x = ° 90x = − °or

26. Example
Solve:
2
10cos 3sin 9 0x x− − + =

27. Example
Solve:
2
sec 5tan 2x x+ = −

28. Important Idea
2 2
sin cos 1x x+ =
2 2
sin 1 cosx x= −
2 2
cos 1 sinx x= −
Trigonometric Identities:
2 2
tan 1 secx x+ =
2 2
1 cot cscx x+ =
See
section 6.5
of your text
for
additional
trig

29. Important Idea
2
4
2
b b ac
x
a
− ± −
=
2
0ax bx c+ + =for
The quadratic formula:

30. Try This
Solve for principal values
in radians:
2
sec 2tan 3x x− =
x=1.220 and x= -.632

31. Important Idea
When solving trig identities,
try one or more of the
following:
•Factor if possible
•Use quadratic formula if you
can’t factor
•Use identities to write the
equation in terms of only one
trig function.

32. Lesson Close
Trignometric equations are
used in science and
engineering.