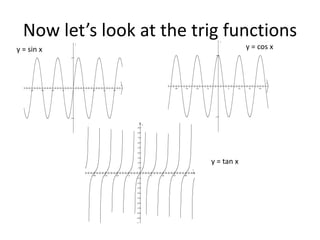
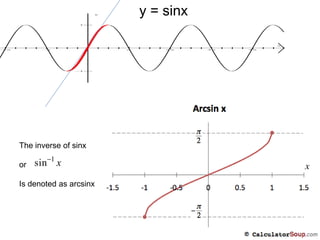
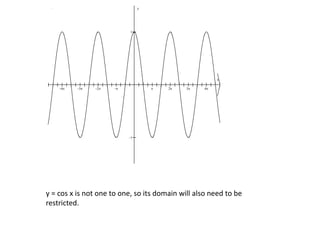
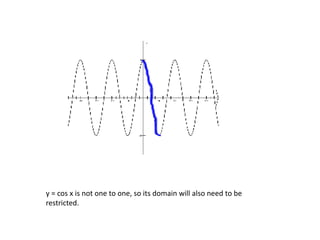
1) For inverse trigonometric functions to exist, the original trigonometric function must be one-to-one. This means that each input has a single, unique output and vice versa. 2) The sine and cosine functions are not one-to-one over their entire domains, so their domains must be restricted for the inverses to be defined. Restricting the domain of sine to [-π/2, π/2] and cosine to [0, π] makes them one-to-one. 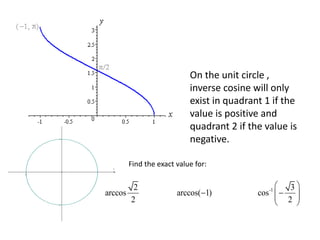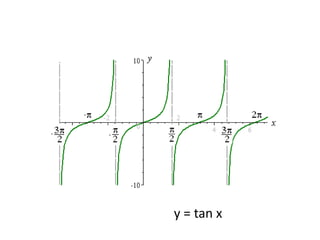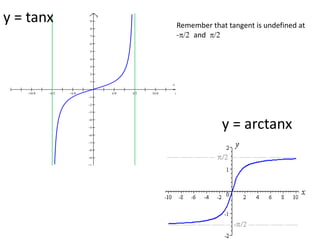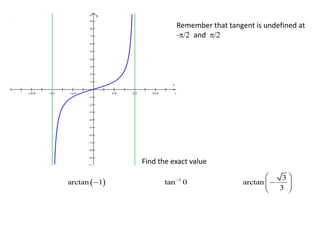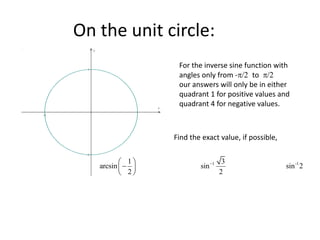3) The inverse functions are denoted as arcsine, arccosine, and arctangent. Their values are restricted to certain quadrants based on the corresponding trigon

1. 4.7 INVERSE TRIGONOMETRIC
FUNCTIONS

2. For an inverse to exist the function MUST
be one- to - one
• A function is one-to-
one if for every x there
is exactly one y and
for every y there is
exactly one x.
• So
• If x and/or y is raised
to an even power then
the inverse does not
exist unless the
domain is restricted.

3. • The equation y = x2
• does not have an
inverse because two
different x values will
produce the same y-
value.
• i.e. x = 2 and x = -2 will
produce y = 4.
• The horizontal line
test fails.
• In order to restrict the
domain, a basic
knowledge of the
shape of the graph is
crucial. This is a
parabola with (0,0) as
the vertex. Restrict
the domain to the
interval [0,infinity) to
make it one-to-one.

4. Now let’s look at the trig functions
       


x
y
       


x
y
       



















x
y
y = sin x y = cos x
y = tan x

5.        


x
y
For the graph of y = sin x, the Domain is (-∞, ∞)
the Range is [-1, 1]
Not a 1-1 function
So it currently does
not have an inverse

6.        


x
y
However we can restrict the domain to [-/ , /]
Note the range will remain [-1, 1]
Now it’s 1-1!

7. 
 
    



x
y y = sinx
The inverse of sinx
or
Is denoted as arcsinx
x
1
sin

8. On the unit circle:
 


x
y
For the inverse sine function with
angles only from -/ to /
our answers will only be in either
quadrant 1 for positive values and
quadrant 4 for negative values.
Find the exact value, if possible,
1 -1
1 3
arcsin sin sin 2
2 2

 

 
 

9.        


x
y
y = cos x is not one to one, so its domain will also need to be
restricted.

10. y = cos x is not one to one, so its domain will also need to be
restricted.

11. / / / /  / / 


x
y
On this interval, [0, ] the
cosine function is one-to-
one and we can now
define the inverse cosine
function.
y = arccos x or y = cos-1 x
y = arccos x
y = cos x

12. On the unit circle ,
inverse cosine will only
exist in quadrant 1 if the
value is positive and
quadrant 2 if the value is
negative.
 


x
y
Find the exact value for:
-1
2 3
arccos arccos( 1) cos
2 2
 
 
 
 
 

13. y = tan x

14. / / / / / / 



















x
y
Remember that tangent is undefined at
-/ and /
y = tanx
y = arctanx

15. / / / / / / 



















x
y
Remember that tangent is undefined at
-/ and /
Find the exact value
  1 3
arctan 1 tan 0 arctan
3

 
 
 
 
 

16. Using the calculator.
• Be in radian mode
• Arctan(-15.7896)
• Arcsin(.3456)
• Arccos(-.6897)
• Arcsin(1.4535)
• Arccos(-2.4534)

17. H Dub
• 4-7 Page 349 #1-16all, 49-67odd