This document discusses stretching, shrinking, and reflecting graphs of functions. It defines vertical stretching as multiplying the y-values by a constant factor c greater than 1, vertically shrinking as multiplying by a constant less than 1, and reflecting as changing the sign of either the x- or y-values. Examples are given of reflecting a graph across the x- or y-axis. The order of transformations matters, as applying them in a different sequence results in a different equation. Finding the equation of a transformed graph from its shifts on a calculator graph is also demonstrated.

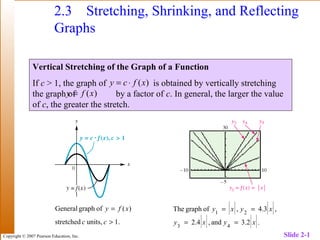
1. Copyright © 2007 Pearson Education, Inc. Slide 2-1
2.3 Stretching, Shrinking, and Reflecting
Graphs
Vertical Stretching of the Graph of a Function
If c > 1, the graph of is obtained by vertically stretching
the graph of by a factor of c. In general, the larger the value
of c, the greater the stretch.
)(xfcy ⋅=
)(xfy =
.1units,stretched
)(ofgraphGeneral
>
=
cc
xfy
.2.3and,4.2
,3.4,ofgraphThe
43
21
xyxy
xyxy
==
==

2. Copyright © 2007 Pearson Education, Inc. Slide 2-2
2.3 Vertical Shrinking
Vertical Shrinking of the Graph of a Function
If the graph of is obtained by vertically shrinking
the graph of by a factor of c. In general, the smaller the value
of c, the greater the shrink.
,10 << c )(xfcy ⋅=
)(xfy =
.10units,shrunk
)(ofgraphGeneral
<<
=
cc
xfy
.
3
4
3
3
3
2
3
1
3.and,5.
,1.,ofgraphThe
xyxy
xyxy
==
==

3. Copyright © 2007 Pearson Education, Inc. Slide 2-3
2.3 Reflecting Across an Axis
Reflecting the Graph of a Function Across an Axis
For a function
(a) the graph of is a reflection of the graph of f across the x-axis.
(b) the graph of is a reflection of the graph of f across the y-axis.
)(xfy −=
),(xfy =
)( xfy −=

4. Copyright © 2007 Pearson Education, Inc. Slide 2-4
2.3 Example of Reflection
Given the graph of sketch the graph of
(a) (b)
Solution
(a) (b)
),(xfy =
)(xfy −= )( xfy −=
).,(isso
,graphon theis),(pointIf
ba
ba
−
If point ( , ) is on the graph,
so is ( , ).
a b
a b−

5. Copyright © 2007 Pearson Education, Inc. Slide 2-5
2.3 Reflection with the Graphing Calculator
).(
and,
,126Set
13
12
2
1
xyy
yy
xxy
−=
−=
++=
.andofgraphthehaveWe 21 yy
.andofgraphthehaveWe 31 yy

6. Copyright © 2007 Pearson Education, Inc. Slide 2-6
2.3 Combining Transformations of Graphs
Example
Describe how the graph of can be obtained by
transforming the graph of Sketch its graph.
Solution
Since the basic graph is the vertex of the parabola is
shifted right 4 units. Since the coefficient of is –3,
the graph is stretched vertically by a factor of 3 and then reflected
across the x-axis. The constant +5 indicates the vertex shifts up 5
units.
5)4(3 2
+−−= xy
.2
xy =
,2
xy =
2
)4( −x
2
)4(3 −− x
2
) 53( 4xy −−= +
shift 4
units
right
shift 5
units up
vertical stretch
by a factor of
3
reflect across
the x-axis

7. Copyright © 2007 Pearson Education, Inc. Slide 2-7
Graphs:
5)4(3 2
+−−= xy
2
( 4)y x= − 2
3( 4)y x= −
2
3( 4)y x= − −

8. Copyright © 2007 Pearson Education, Inc. Slide 2-8
2.3 Caution in Translations of Graphs
• The order in which transformations are made is
important. If they are made in a different order, a
different equation can result.
– For example, the graph of is obtained by
first stretching the graph of by a factor of 2, and
then translating 3 units upward.
– The graph of is obtained by first
translating horizontally 3 units to the left, and then
stretching by a factor of 2.
32 += xy
xy =
32 += xy

9. Copyright © 2007 Pearson Education, Inc. Slide 2-9
2.3 Transformations on a Calculator-
Generated Graph
Example
The figures show two views of the graph and another graph
illustrating a combination of transformations. Find the equation of the
transformed graph.
Solution
The first view indicates the lowest point is (3,–2), a shift 3 units to the
right and 2 units down. The second view shows the point (4,1) on the
graph of the transformation. Thus, the slope of the ray is
Thus, the equation of the transformed graph is
xy =
First View Second View
.3
1
3
43
12
=
−
−
=
−
−−
=m
.233 −−= xy

10. Copyright © 2007 Pearson Education, Inc. Slide 2-9
2.3 Transformations on a Calculator-
Generated Graph
Example
The figures show two views of the graph and another graph
illustrating a combination of transformations. Find the equation of the
transformed graph.
Solution
The first view indicates the lowest point is (3,–2), a shift 3 units to the
right and 2 units down. The second view shows the point (4,1) on the
graph of the transformation. Thus, the slope of the ray is
Thus, the equation of the transformed graph is
xy =
First View Second View
.3
1
3
43
12
=
−
−
=
−
−−
=m
.233 −−= xy