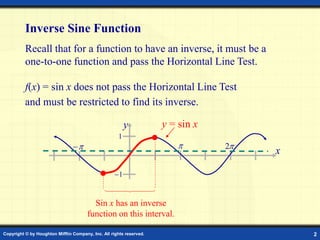
This document discusses inverse trigonometric functions including the inverse sine, cosine, and tangent functions. It defines each inverse function, describes their domains and ranges, and provides examples of evaluating inverse trig functions and compositions of inverse trig functions. The key points are: - The inverse sine is defined as the angle whose sine is x and has a domain of [-1,1] and range of [-π/2, π/2]. 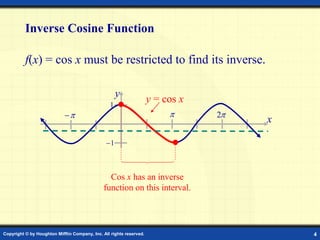- The inverse cosine is defined as the angle whose cosine is x and has a domain of [-1,1] and range of [0, π]. - The inverse tangent is defined as the angle whose tangent is x and has a domain of all real numbers and range

1. Inverse Trigonometric
Functions
Std. XII Maths

2. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2
Inverse Sine Function
y

 
2

1

1
x
y = sin x
Sin x has an inverse
function on this interval.
Recall that for a function to have an inverse, it must be a
one-to-one function and pass the Horizontal Line Test.
f(x) = sin x does not pass the Horizontal Line Test
and must be restricted to find its inverse.

3. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3
The inverse sine function is defined by
y = arcsin x if and only if sin y = x.
Angle whose sine is x
The domain of y = arcsin x is [–1, 1].
Example:
1
a. arcsin
2 6

 1
is the angle whose sine is .
6 2

1 3
b. sin
2 3


 3
sin
3 2
 
This is another way to write arcsin x.
The range of y = arcsin x is [–/2 , /2].

4. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4
Inverse Cosine Function
Cos x has an inverse
function on this interval.
f(x) = cos x must be restricted to find its inverse.
y

 
2

1

1
x
y = cos x

5. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5
The inverse cosine function is defined by
y = arccos x if and only if cos y = x.
Angle whose cosine is x
The domain of y = arccos x is [–1, 1].
Example:
1
a.) arccos
2 3

 1
is the angle whose cosine is .
3 2

1 3 5
b.) cos
2 6

  
 
 
 
3
5
cos
6 2
  
This is another way to write arccos x.
The range of y = arccos x is [0 , ].

6. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 6
Inverse Tangent Function
f(x) = tan x must be restricted to find its inverse.
Tan x has an inverse
function on this interval.
y
x
2
3

2
3
2

2


y = tan x

7. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7
The inverse tangent function is defined by
y = arctan x if and only if tan y = x.
Angle whose tangent is x
Example:
3
a.) arctan
3 6

 3
is the angle whose tangent is .
6 3

1
b.) tan 3
3


 tan 3
3
 
This is another way to write arctan x.
The domain of y = arctan x is .
( , )
 
The range of y = arctan x is [–/2 , /2].

8. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 8
Graphing Utility: Graph the following inverse functions.
a. y = arcsin x
b. y = arccos x
c. y = arctan x
–1.5 1.5
–

–1.5 1.5
2
–
–3 3

–
Set calculator to radian mode.

9. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9
Graphing Utility: Approximate the value of each expression.
a. cos–1 0.75 b. arcsin 0.19
c. arctan 1.32 d. arcsin 2.5
Set calculator to radian mode.

10. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10
Composition of Functions:
f(f –1(x)) = x and (f –1(f(x)) = x.
If –1  x  1 and – /2  y  /2, then
sin(arcsin x) = x and arcsin(sin y) = y.
If –1  x  1 and 0  y  , then
cos(arccos x) = x and arccos(cos y) = y.
If x is a real number and –/2 < y < /2, then
tan(arctan x) = x and arctan(tan y) = y.
Example: tan(arctan 4) = 4
Inverse Properties:

11. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 11
Example:
a. sin–1(sin (–/2)) = –/2
 
1 5
b. sin sin
3

  
 
 
5
3
 does not lie in the range of the arcsine function, –/2  y  /2.
y
x
5
3

3


5 2
3 3
 

  
However, it is coterminal with
which does lie in the range of the arcsine
function.
   
1 1
5
sin sin sin sin
3 3 3
  
 
   
   
   
   

12. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 12
Example:
 
2
Find the exact value of tan arccos .
3
x
y
3
2
adj
2 2
Let =arccos , thencos .
3 hyp 3
u u  
2 2
3 2 5
 
  opp 5
2
tan arccos tan
3 adj 2
u
  
u

13. EXTRA QUESTIONS
• INVERSE TRIG. QUEST.docx
Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 13