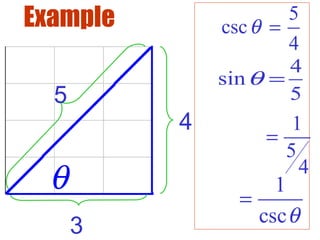
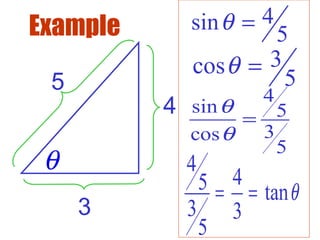
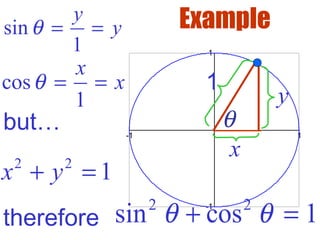
- Basic trigonometric identities relate trigonometric functions of the same angle. They allow one trig function to be substituted for another equivalent expression. - The basic reciprocal, quotient, and Pythagorean identities are introduced and examples are given of using identities to simplify trigonometric expressions. - It is important to be able to use multiple identities together to solve problems involving trigonometric functions of an angle.

1. 6-5: Basic Trigonometric
Identities
© 2007 Roy L. Gover (www.mrgover.com)
Learning Goals:
•Develop the basic trig
identities
•Simplify trig expressions

2. Definition
A trigonometric identity is a
statement of equality
between two expressions.
It means one expression
can be used in place of the
other.
A list of the basic identities
can be found on p.460 of
your text.

3. Example
θ
4
3
5
5
csc
4
θ =
4
sin
5
θ =
1
5
4
=
1
cscθ
=

4. Definition
1
sin
csc
θ
θ
=
1
csc
sin
θ
θ
=
1
cos
sec
θ
θ
=
1
sec
cos
θ
θ
=
1
cot
tan
θ
θ
=
1
tan
cot
θ
θ
=
Reciprocal Identities:

5. Example
If , find
1
sin
2
A = csc A

6. Try This
If , find
3
cos
4
β = sec β
4
sec
3
β =

7. 4
3
5
Example 4sin
5
θ =
3cos
5
θ =
4
sin 5
3cos
5
θ
θ
=
4
45 tan
3 3
5
θ= =
θ

8. Definition
cos
cot
sin
A
A
A
=
sin
tan
A
A
cosA
=
sin cos tanA A A⇒ =
Quotient Identities:
cos sin cotA A A⇒ =

9. Example
If &
1
sin
2
A =
tan A
2
cos
3
A =
find

10. Try This
If &
1
cos
2
A = tan 2A =
find sin A
sin 1A =

11. -1 1
-1
1
θ
x
y
1
sin
1
y
yθ = =
cos
1
x
xθ = =
but…
2 2
1x y+ =
therefore
2 2
sin cos 1θ θ+ =
Example

12. Definition
2 2
sin cos 1θ θ+ =
Divide by to get:
2
cos θ
2 2
tan 1 secθ θ+ =
Pythagorean Identities:

13. Definition
2 2
sin cos 1θ θ+ =
Pythagorean Identities:
Divide by to get:
2
sin θ
2 2
1 cot cscθ θ+ =

14. Example
Use the Pythagorean
Identities to simplify the
given expression:
2 2 2
tan cos cost t t+

15. Example
Use the Identities to
simplify the given
expression:
2 2 2
tan cos cost t t+

16. Try This
Use the Identities to
simplify the given
expression:
2 2 2
cot sin sint t t+
1

17. Try This
Use the
Identities
to simplify
the given
expression
:
2 2
2
sec tan
cos
t t
t
−
2
sec t

18. Example
Use the
Pythagorean
Identities to find
sin t for the given
value of cos t.
Make sure the
sign is correct for
the given
quadrant.
3
cos
10
t = −
2
t
π
π< <

19. Try This
Use the
Pythagorean
Identities to find
sin t for the given
value of cos t.
Make sure the
sign is correct for
the given
quadrant.
2
cos
5
t =
3
2
2
t
π
π< <
5
5
−

20. Example
If , find
3
tan
5
A = cos A
first find …sec A

21. Important Idea
To solve trigonometric
identity problems, you
may use more than one
identity in the same
problem.

22. Try This
If , find
2
cos
3
θ = tanθ
Assume θ is between 0 & 2
π
5
tan
2
θ =

23. Example
If and t is in
quadrant I, find the 5
remaining trig functions.
cos .3586t =

24. Try This
If
and t is in
quadrant II,
find the 5
remaining trig
functions.
sin .2985t = cos .9544t = −
tan .3128t = −
sec 1.0478t = −
csc 3.3501t =
cot 3.1969t = −

25. Example
Simplify:
2 2
2
sin cos
cos
A A
A
+

26. Try This
Simplify:
tan cscB B
sec B

27. Example
Simplify:
cos
sec tan
θ
θ θ−

28. Lesson Close
From memory, name one trig
identity we studied today.