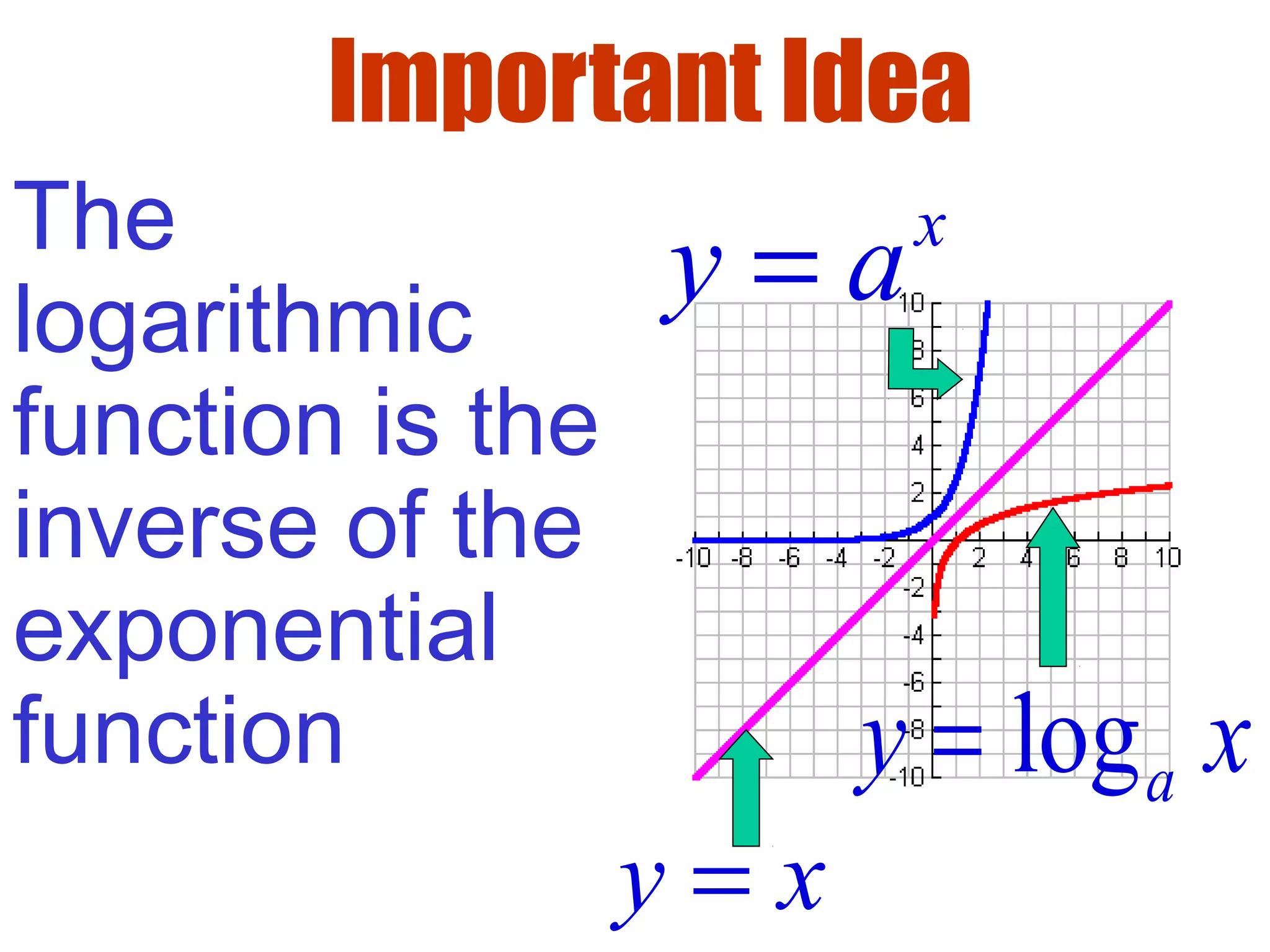
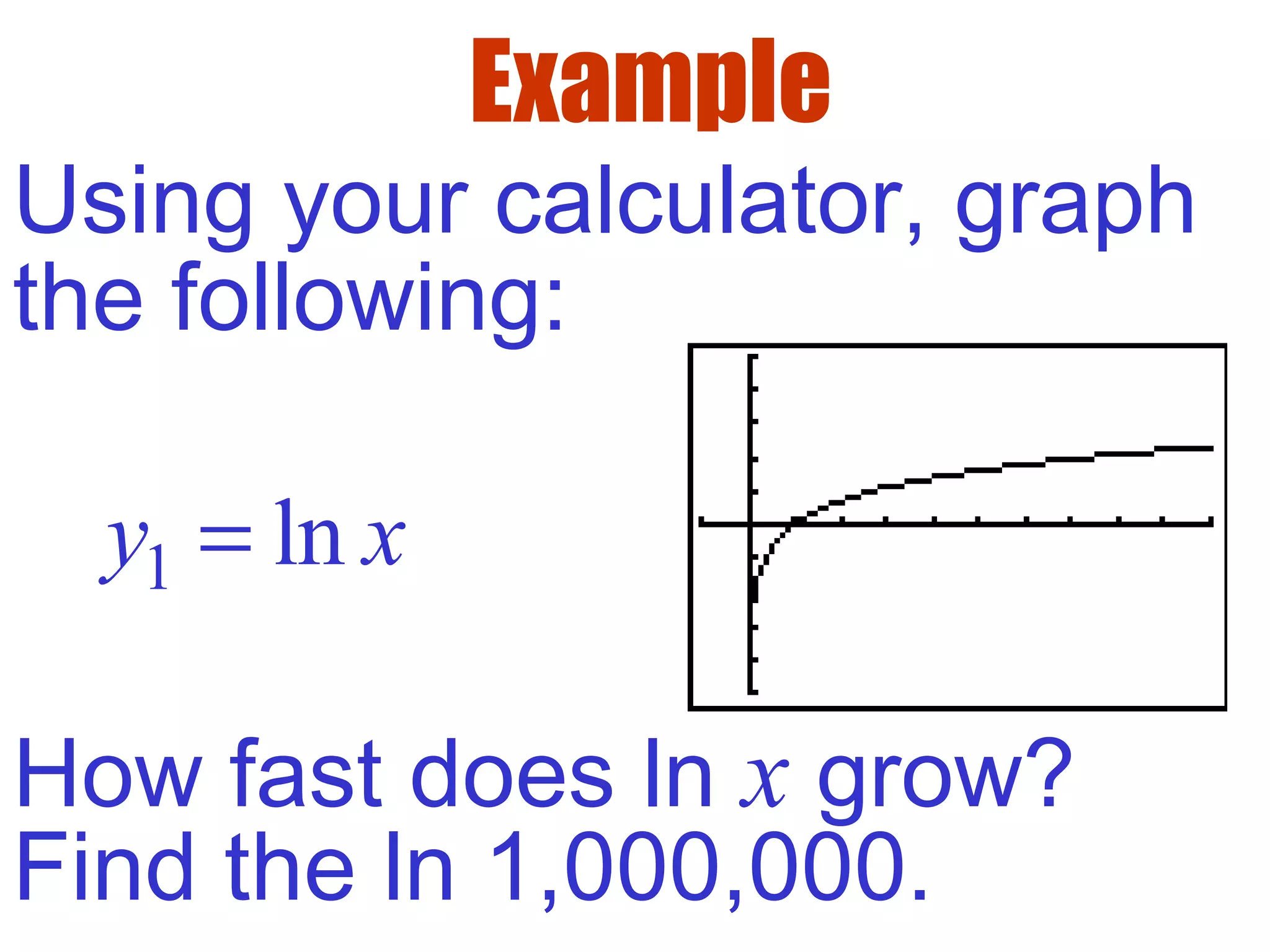
This document defines common (base 10) and natural (base e) logarithms and explains how to evaluate, solve equations involving, and graph logarithmic functions. It also discusses important properties of logarithms including: - Logarithms are the inverse functions of exponentials. - The natural logarithm ln(x) is the logarithm with base e, where e is an important mathematical constant approximately equal to 2.718. 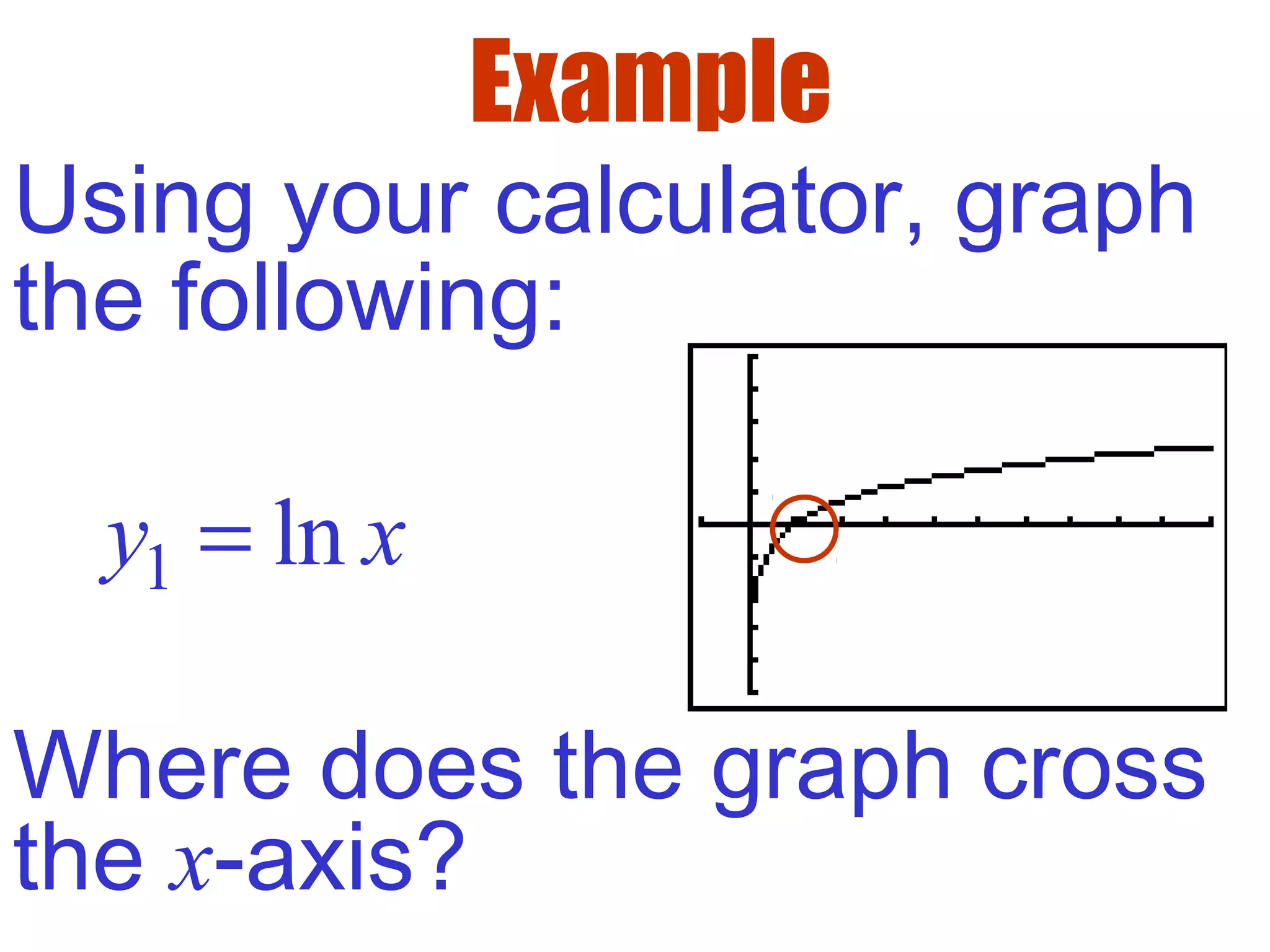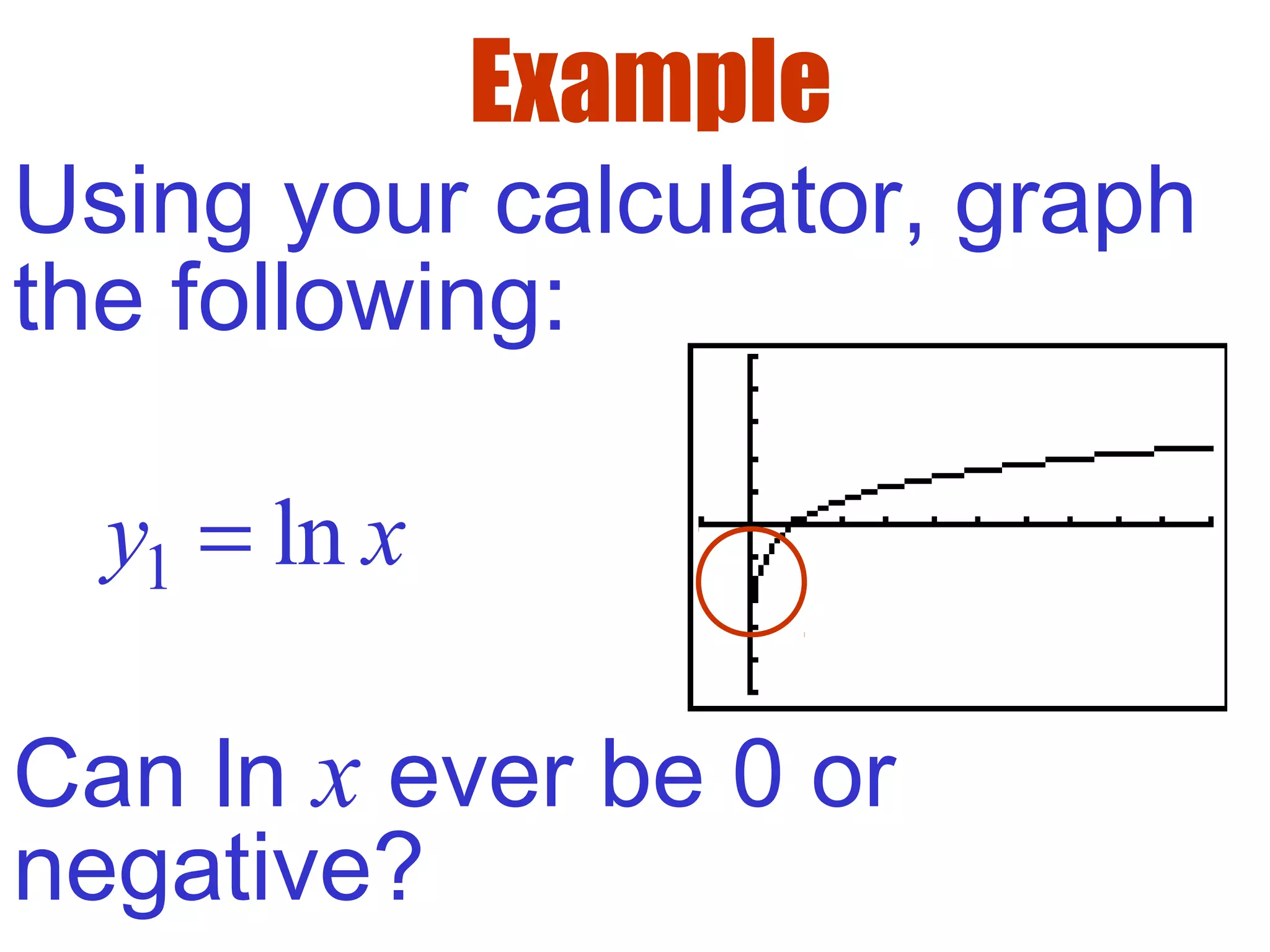- The domain of ln(x) is x > 0, since it is undefined for non-positive values. The range extends from -∞ to ∞.

1. 5.4: Common & Natural
Logarithmic Functions
© 2008 Roy L. Gover(www.mrgover.com)
Learning Goals:
•Evaluate common and
natural logarithms
•Solve logarithmic
equations

2. Definition
logay x=
if and
only if
y=log
base a of x
y
a x=

3. Important Idea
logay x= Logarithmic
Form
Exponential
Form
y
a x=

4. The
logarithmic
function is the
inverse of the
exponential
function
y x=
Important Idea
x
y a=
logay x=

5. Example
Write the following
logarithmic function in
exponential form:
10log 0.01 2= −
5log 25 2=
3
1
log 3
27
 
= − 
 
6log 6 1=

6. Try This
Write the following
logarithmic function in
exponential form:
2
10 100=10log 100 2=
2 1
5
25
−
=5
1
log 2
25
 
= − 
 

7. Important Idea
In your book and
on the calculator,
is
the same
as . If no
base is stated, it
is understood that
the base is 10.
10log x
log x

8. Example
Without using your
calculator, find each value:
log1000
log1
log 10
log( 3)−

9. Try This
Without using your
calculator, find each value:
log100,000
log10
3
log 10
log( 7)−
5
1
1/3
undefined

10. Example
Solve each equation by using
an equivalent statement:
log 2x =
10 29x
=

11. Try This
Solve each equation by using
an equivalent statement:
log 3x =
10 52x
=
x=1000
x=1.716

12. Definition
A second type of logarithm
exists, called the natural
logarithm and written ln x,
that uses the number e as a
base instead of the number
10. The natural logarithm is
very useful in science and
engineering.

13. Important Idea
Like , the
number e is a
very important
number in
mathematics.
π

14. Important Idea
ln x
The natural logarithm is a
logarithm with the base e
is a short way of
writing: loge x

15. Definition
ln x y=
y
e x=
If and
only if
ln logex x=

16. Example
ln 0.0198
Use a calculator to find
the following value to the
nearest ten-thousandth:

17. Try This
1
ln
0.32
 
 
 
Use a calculator to find the
following value to the
nearest ten-thousandth:
1.1394

18. Example
Solve each equation by using
an equivalent statement:
ln 4x =
5x
e =

19. Try This
Solve each equation by using
an equivalent statement:
ln 2x = x=7.389
x=2.0798x
e =

20. Example
Using your calculator, graph
the following:
1 lny x=
Where does the graph cross
the x-axis?

21. Example
Using your calculator, graph
the following:
1 lny x=
Can ln x ever be 0 or
negative?

22. Example
Using your calculator, graph
the following:
1 lny x=
What is the domain and
range of ln x?

23. Example
Using your calculator, graph
the following:
1 lny x=
How fast does ln x grow?
Find the ln 1,000,000.

24. Try This
Using your calculator, graph:
1 lny x=
2 ln( 3)y x= −
3 ln( 3) 5y x= − +
Describe the differences.
How does the domain and
range change?

25. Lesson Close
A logarithm is an
exponent. Illustrate with
an example why this is
so.