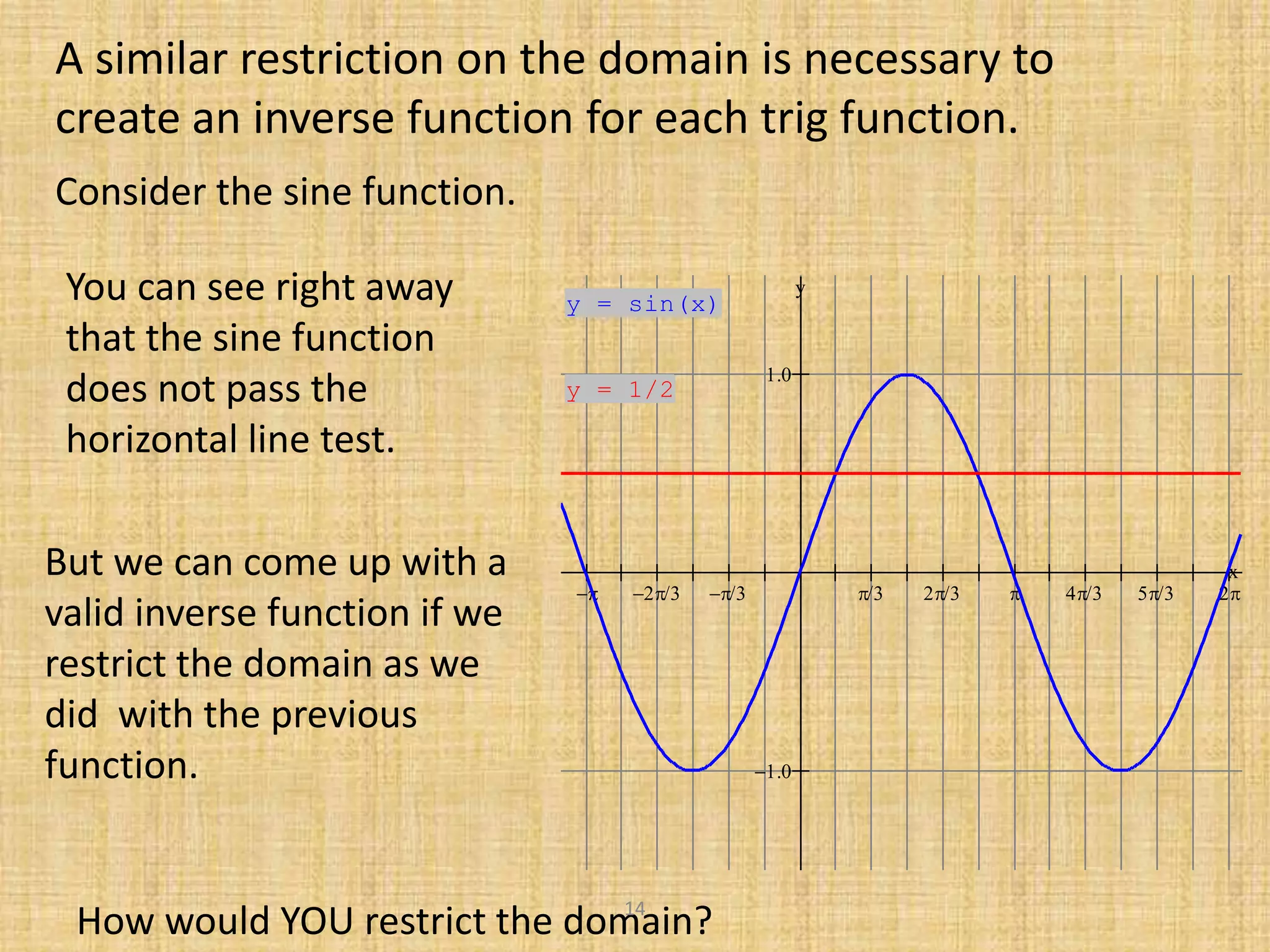
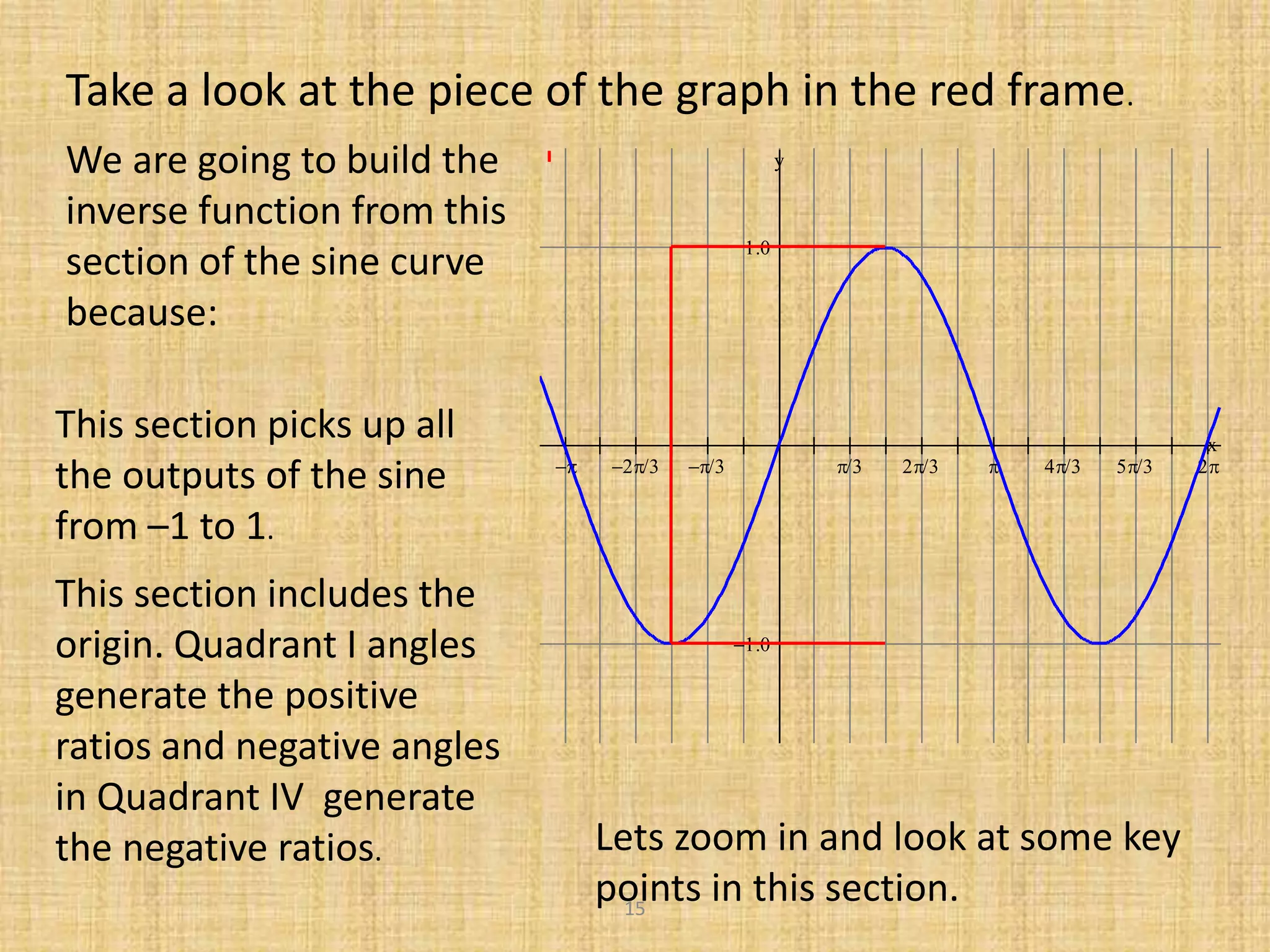
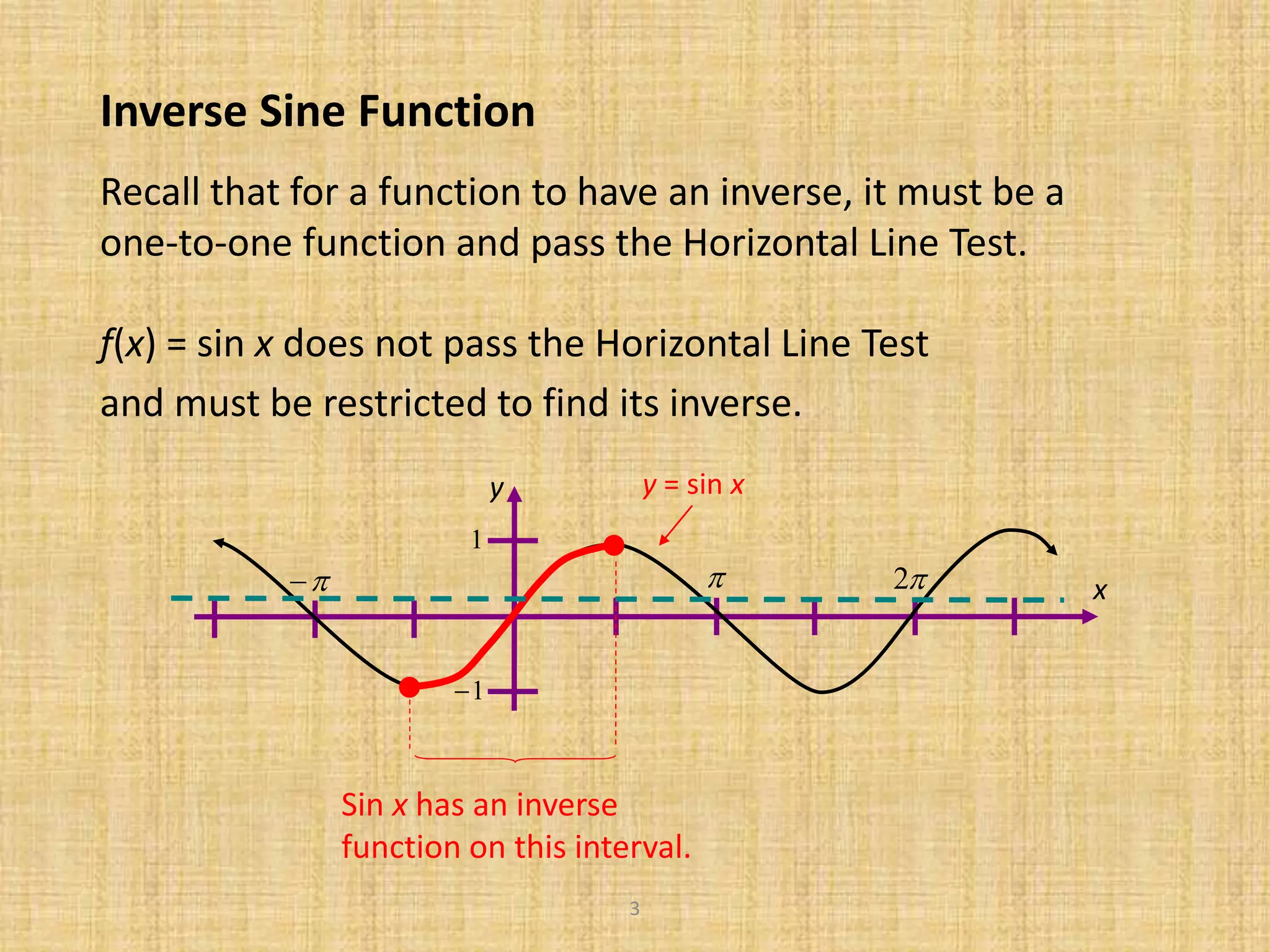
1) The document discusses inverse trigonometric functions including the inverse sine, cosine, and tangent functions. 2) It defines each inverse function and describes how the domain of the original trig function must be restricted to define the inverse. 3) Examples are provided to demonstrate evaluating inverse trig functions and their compositions with the original trig functions.

1. Inverse Trigonometric
Functions

3. 3
Inverse Sine Function
y
 2
1
1
x
y = sin x
Sin x has an inverse
function on this interval.
Recall that for a function to have an inverse, it must be a
one-to-one function and pass the Horizontal Line Test.
f(x) = sin x does not pass the Horizontal Line Test
and must be restricted to find its inverse.

4. 4
The inverse sine function is defined by
y = arcsin x if and only if sin y = x.
Angle whose sine is x
The domain of y = arcsin x is [–1, 1].
Example:
1a. arcsin
2 6
 1is the angle whose sine is .
6 2

1 3b. sin
2 3

 3sin
3 2
 
This is another way to write arcsin x.
The range of y = arcsin x is [–/2 , /2].

5. 5
Inverse Cosine Function
Cos x has an inverse
function on this interval.
f(x) = cos x must be restricted to find its inverse.
y
 2
1
1
x
y = cos x

6. 6
The inverse cosine function is defined by
y = arccos x if and only if cos y = x.
Angle whose cosine is x
The domain of y = arccos x is [–1, 1].
Example:
1a.) arccos
2 3
 1is the angle whose cosine is .
3 2

1 3 5b.) cos
2 6
  
  
 
35cos
6 2
  
This is another way to write arccos x.
The range of y = arccos x is [0 , ].

7. 7
Inverse Tangent Function
f(x) = tan x must be restricted to find its inverse.
Tan x has an inverse
function on this interval.
y
x
2
3
2
3
2

2

y = tan x

8. 8
The inverse tangent function is defined by
y = arctan x if and only if tan y = x.
Angle whose tangent is x
Example:
3a.) arctan
3 6
 3is the angle whose tangent is .
6 3

1
b.) tan 3
3

 tan 3
3
 
This is another way to write arctan x.
The domain of y = arctan x is .( , ) 
The range of y = arctan x is [–/2 , /2].

9. 9
Composition of Functions:
f(f –1(x)) = x and (f –1(f(x)) = x.
If –1  x  1 and – /2  y  /2, then
sin(arcsin x) = x and arcsin(sin y) = y.
If –1  x  1 and 0  y  , then
cos(arccos x) = x and arccos(cos y) = y.
If x is a real number and –/2 < y < /2, then
tan(arctan x) = x and arctan(tan y) = y.
Example: tan(arctan 4) = 4
Inverse Properties:

10. 10
a. sin–1(sin (–/2)) = –/2
 1 5b. sin sin
3
  
  
5
3
 does not lie in the range of the arcsine function, –/2  y  /2.
y
x
5
3

3

5 2
3 3
   However, it is coterminal with
which does lie in the range of the arcsine
function.
   1 15sin sin sin sin
3 3 3
         
      
EXAMPLES:

11. 11
 2Find the exact value of tan arccos .
3
x
y
3
2
adj2 2Let =arccos , thencos .
3 hyp 3
u u  
2 2
3 2 5 
  opp 52tan arccos tan
3 adj 2
u  
u
EXAMPLES:

12. Consider the graph of .2
xy 
 





x
y
Note the two points on
the graph and also on
the line y=4.
f(2) = 4 and f(-2) = 4 so
what is an inverse
function supposed to do
with 4?
?2)4(2)4( 11
 
forf
By definition, a function cannot generate two different outputs for
the same input, so the sad truth is that this function, as is, does not
have an inverse. 12

13. So how is it that we arrange for this function to have an
inverse?
We consider only one half of
the graph: x > 0.
The graph now passes the
horizontal line test and we do
have an inverse:
xxf
xforxxf



)(
0)(
1
2
Note how each graph reflects across the line y = x onto its inverse.
xy 
   
x
4
y=x
2
xy 
2
13

14. A similar restriction on the domain is necessary to
create an inverse function for each trig function.
Consider the sine function.
You can see right away
that the sine function
does not pass the
horizontal line test.
But we can come up with a
valid inverse function if we
restrict the domain as we
did with the previous
function.
How would YOU restrict the domain?
        


x
y
y = sin(x)
y = 1/2
14

15. Take a look at the piece of the graph in the red frame.
        


x
yWe are going to build the
inverse function from this
section of the sine curve
because:
This section picks up all
the outputs of the sine
from –1 to 1.
This section includes the
origin. Quadrant I angles
generate the positive
ratios and negative angles
in Quadrant IV generate
the negative ratios. Lets zoom in and look at some key
points in this section.15

16.      


x
y
y = sin(x)
1
2
2
3
3
2
2
4
2
1
6
00
2
1
6
2
2
4
2
3
3
1
2
)(












xfx
I have plotted the special angles on the curve and the
table.
16

17. 1
2
3

30

60

45

45 1
2
2
The graphs give you the big picture concerning the
behavior of the inverse trig functions. Calculators are
helpful with calculations (later for that). But special
triangles can be very helpful with respect to the basics.
Use the special triangles above to answer the following. Try to figure
it out yourself before you click.










)2(csc
2
3
arccos
1
 
  21/230csc
6
30
2
3
30cos
6
30














becauseor
becauseor



18. 1
2
3

30

60

45

45 1
2
2
OK, lets try a few more. Try them before you peek.





 








2
1
arcsin
)3(tan
2
1
arcsin
1
 
2
1
45sin)
4
(45
3
1
3
60tan)
3
(60
2
1
45sin)
4
(45









becauseor
becauseor
becauseor


