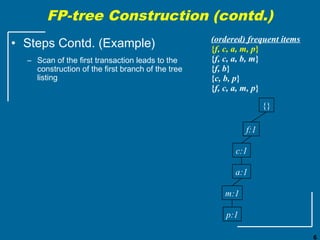
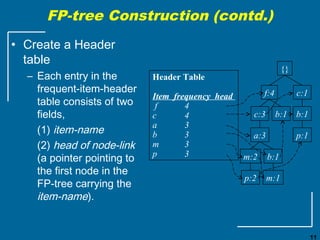
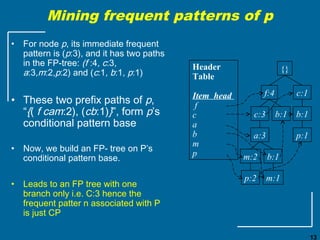
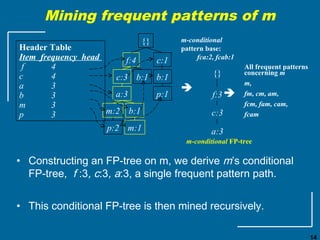
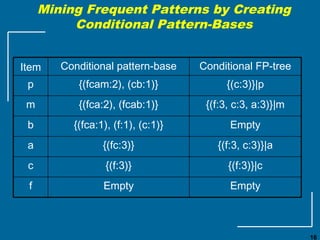
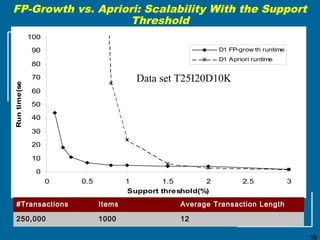
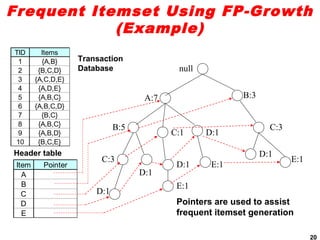
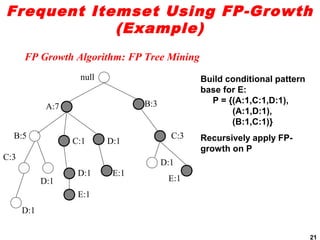
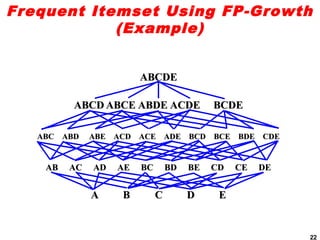
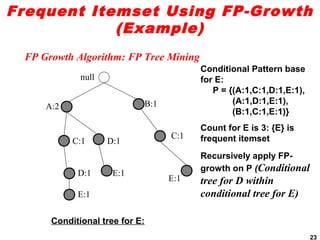
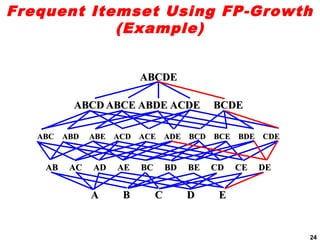
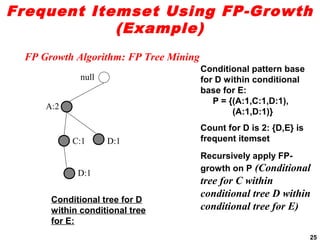
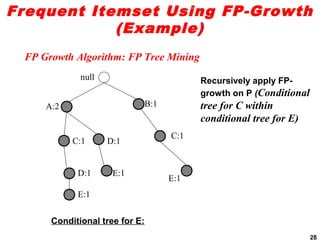
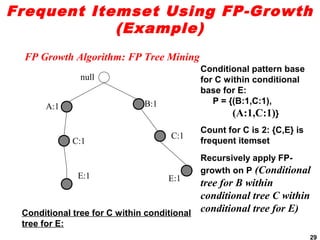
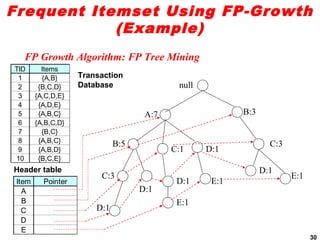
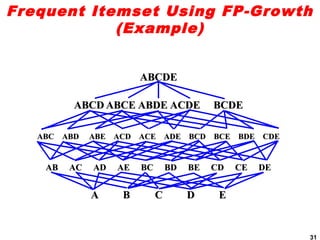
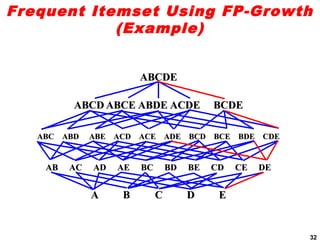
The document discusses the FP-growth algorithm for mining frequent patterns without candidate generation. It begins with an overview of the performance bottlenecks of the Apriori algorithm and introduces the FP-growth approach. The key steps of FP-growth include compressing the transaction database into a frequent-pattern tree (FP-tree) structure, and then mining the FP-tree to find all frequent patterns. The mining process recursively constructs conditional FP-trees to decompose the problem into smaller sub-problems without candidate generation. Examples are provided to illustrate the FP-tree construction and pattern mining.

1. Data Mining
Spring 2007
• Frequent-Pattern Tree Approach
Towards ARM
Lecture 11-12

2. 2
In this lecture
The lecture is based on
• Jiawei Han, Jian Pei, Yiwen Yin And Runying Mao Data,
“Mining Frequent Patterns without Candidate
Generation: A Frequent-Pattern Tree Approach”,
Mining and Knowledge Discovery, Kluwer Academic
Publishers, 2004
• Jiawei Han, Jian Pei, Yiwen Yin, “Mining Frequent
Patterns without Candidate Generation”, In Proc. 2000
ACM SIGMOD Int. Conf. Management of Data (SIGMOD’00), Dallas,
TX, pp. 1–12.
Some slides are adapted from official text book slides of
• Jiawei Han and Micheline Kamber, “Data Mining: Concepts and
Techniques”, Morgan Kaufmann Publishers, August 2000

3. 3
Is Apriori Fast Enough? — Performance
Bottlenecks
• The core of the Apriori algorithm:
– Use frequent (k – 1)-itemsets to generate candidate frequent k-
itemsets
– Use database scan and pattern matching to collect counts for the
candidate itemsets
• The bottleneck of Apriori: candidate generation
– Huge candidate sets:
• 104
frequent 1-itemset will generate 107
candidate 2-itemsets
• To discover a frequent pattern of size 100, e.g., {a1, a2, …, a100},
one needs to generate 2100
≈ 1030
candidates.
– Multiple scans of database:
• Needs (n +1 ) scans, n is the length of the longest pattern

4. 4
Mining Frequent Patterns Without
Candidate Generation
• Steps
1. Compress a large database into a compact,
Frequent-Pattern tree (FP-tree) structure
1. highly condensed, but complete for frequent pattern mining
2. avoid costly database scans
2. Develop an efficient, FP-tree-based frequent pattern
mining method
1. A divide-and-conquer methodology: decompose mining
tasks into smaller ones
2. Avoid candidate generation: sub-database test only!

5. 5
FP-tree Construction
Item frequency head
f 4
c 4
a 3
b 3
m 3
p 3
TID Items bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Steps:
1. Scan DB once, find frequent 1-
itemset (single item pattern)
2. Order frequent items in frequency
descending order
3. Scan DB again, construct FP-tree

6. 6
• Steps Contd. (Example)
– Scan of the first transaction leads to the
construction of the first branch of the tree
listing
{}
f:1
c:1
a:1
m:1
p:1
FP-tree Construction (contd.)
(ordered) frequent items
{f, c, a, m, p}
{f, c, a, b, m}
{f, b}
{c, b, p}
{f, c, a, m, p}

7. 7
{}
f:2
c:2
a:2
b:1m:1
p:1 m:1
FP-tree Construction (contd.)
(ordered) frequent items
{f, c, a, m, p}
{f, c, a, b, m}
{f, b}
{c, b, p}
{f, c, a, m, p}
• Steps Contd. (Example)
– Scan of the first transaction leads to the
construction of the first branch of the tree
listing
– Second transaction shares a common prefix
with the existing path the count of each node
along the prefix is incremented by 1
– Two new nodes are created and linked as
children of (a:2) and (b:1) respec.

8. 8
• Steps Contd. (Example)
– Scan of the first transaction leads to the
construction of the first branch of the tree
listing
– Second transaction shares a common prefix
with the existing path the count of each node
along the prefix is incremented by 1
– Two new nodes are created and linked as
children of (a:2) and (b:1) respec.
– Similarly for the third transaction
{}
f:3
b:1c:2
a:2
b:1m:1
p:1 m:1
FP-tree Construction (contd.)
(ordered) frequent items
{f, c, a, m, p}
{f, c, a, b, m}
{f, b}
{c, b, p}
{f, c, a, m, p}

9. 9
• Steps Contd. (Example)
– Scan of the first transaction leads to the
construction of the first branch of the tree
listing
– Second transaction shares a common prefix
with the existing path the count of each node
along the prefix is incremented by 1
– Two new nodes are created and linked as
children of (a:2) and (b:1) respec.
– Similarly for the third transaction
– The scan of the fourth transaction leads to the
construction of the second branch of the tree,
(c:1), (b:1), (p:1).
{}
f:3 c:1
b:1
p:1
b:1c:2
a:2
b:1m:1
p:1 m:1
FP-tree Construction (contd.)
(ordered) frequent items
{f, c, a, m, p}
{f, c, a, b, m}
{f, b}
{c, b, p}
{f, c, a, m, p}

10. 10
• Steps Contd. (Example)
– Scan of the first transaction leads to the
construction of the first branch of the tree
listing
– Second transaction shares a common prefix
with the existing path the count of each node
along the prefix is incremented by 1
– Two new nodes are created and linked as
children of (a:2) and (b:1) respec.
– Similarly for the third transaction
– The scan of the fourth transaction leads to the
construction of the second branch of the tree,
(c:1), (b:1), (p:1).
– For the last transaction, since its frequent item
list is identical to the first one, the path is
shared.
{}
f:4 c:1
b:1
p:1
b:1c:3
a:3
b:1m:2
p:2 m:1
FP-tree Construction (contd.)
(ordered) frequent items
{f, c, a, m, p}
{f, c, a, b, m}
{f, b}
{c, b, p}
{f, c, a, m, p}

11. 11
• Create a Header
table
– Each entry in the
frequent-item-header
table consists of two
fields,
(1) item-name
(2) head of node-link
(a pointer pointing to
the first node in the
FP-tree carrying the
item-name).
FP-tree Construction (contd.)
{}
f:4 c:1
b:1
p:1
b:1c:3
a:3
b:1m:2
p:2 m:1
Header Table
Item frequency head
f 4
c 4
a 3
b 3
m 3
p 3

12. 12
Mining frequent patterns using FP-tree
• Mining frequent patterns out of FP-tree is based
upon following Node-link property
– For any frequent item ai , all the possible patterns
containing only frequent items and ai can be obtained by
following ai ’s node-links, starting from ai ’s head in the
FP-tree header.
• Lets go through an example to understand the full
implication of this property in the mining process.

13. 13
• For node p, its immediate frequent
pattern is (p:3), and it has two paths
in the FP-tree: (f :4, c:3,
a:3,m:2,p:2) and (c:1, b:1, p:1)
• These two prefix paths of p,
“{( f cam:2), (cb:1)}”, form p’s
conditional pattern base
• Now, we build an FP- tree on P’s
conditional pattern base.
• Leads to an FP tree with one
branch only i.e. C:3 hence the
frequent patter n associated with P
is just CP
{}
f:4 c:1
b:1
p:1
b:1c:3
a:3
b:1m:2
p:2 m:1
Header
Table
Item head
f
c
a
b
m
p
Mining frequent patterns of p

14. 14
Mining frequent patterns of m
• Constructing an FP-tree on m, we derive m’s conditional
FP-tree, f :3, c:3, a:3, a single frequent pattern path.
• This conditional FP-tree is then mined recursively.
m-conditional
pattern base:
fca:2, fcab:1
{}
f:3
c:3
a:3
m-conditional FP-tree
All frequent patterns
concerning m
m,
fm, cm, am,
fcm, fam, cam,
fcam


{}
f:4 c:1
b:1
p:1
b:1c:3
a:3
b:1m:2
p:2 m:1
Header Table
Item frequency head
f 4
c 4
a 3
b 3
m 3
p 3

15. 15
Mining frequent patterns of m
{}
f:3
c:3
a:3
m-conditional FP-tree
Cond. pattern base of “am”: (fc:3)
{}
f:3
c:3
am-conditional FP-tree
Cond. pattern base of “cm”: (f:3)
{}
f:3
cm-conditional FP-tree
Cond. pattern base of “cam”: (f:3)
{}
f:3
cam-conditional FP-tree

16. 16
Mining Frequent Patterns by Creating
Conditional Pattern-Bases
EmptyEmptyf
{(f:3)}|c{(f:3)}c
{(f:3, c:3)}|a{(fc:3)}a
Empty{(fca:1), (f:1), (c:1)}b
{(f:3, c:3, a:3)}|m{(fca:2), (fcab:1)}m
{(c:3)}|p{(fcam:2), (cb:1)}p
Conditional FP-treeConditional pattern-baseItem

17. 17
Single FP-tree Path Generation
• Suppose an FP-tree T has a single path P
• The complete set of frequent pattern of T can be
generated by enumeration of all the combinations of the
sub-paths of P
{}
f:3
c:3
a:3
m-conditional FP-tree
All frequent patterns
concerning m
m,
fm, cm, am,
fcm, fam, cam,
fcam


18. 18
Why Is Frequent Pattern Growth
Fast?
• Our performance study shows
– FP-growth is an order of magnitude faster than Apriori, and is
also faster than tree-projection
• Reasoning
– No candidate generation, no candidate test
– Use compact data structure
– Eliminate repeated database scan
– Basic operation is counting and FP-tree building

19. 19
FP-Growth vs. Apriori: Scalability With the Support
Threshold
0
10
20
30
40
50
60
70
80
90
100
0 0.5 1 1.5 2 2.5 3
Support threshold(%)
Runtime(sec.)
D1 FP-grow th runtime
D1 Apriori runtime
Data set T25I20D10K
#Transactions Items Average Transaction Length
250,000 1000 12

20. 20
null
A:7
B:5
B:3
C:3
D:1
C:1
D:1
C:3
D:1
D:1
E:1
E:1
TID Items
1 {A,B}
2 {B,C,D}
3 {A,C,D,E}
4 {A,D,E}
5 {A,B,C}
6 {A,B,C,D}
7 {B,C}
8 {A,B,C}
9 {A,B,D}
10 {B,C,E}
Pointers are used to assist
frequent itemset generation
D:1
E:1
Transaction
Database
Item Pointer
A
B
C
D
E
Header table
Frequent Itemset Using FP-Growth
(Example)

21. 21
null
A:7
B:5
B:3
C:3
D:1
C:1
D:1
C:3
D:1
E:1
D:1
E:1
Build conditional pattern
base for E:
P = {(A:1,C:1,D:1),
(A:1,D:1),
(B:1,C:1)}
Recursively apply FP-
growth on P
E:1
D:1
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

22. 22
AA BB CC DD EE
AB AC AD AE BC BD BE CD CE DEAB AC AD AE BC BD BE CD CE DE
ABC ABD ABE ACD ACE ADE BCD BCE BDE CDEABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
ABCDABCD ABCEABCE ABDEABDE ACDE BCDEACDE BCDE
ABCDEABCDE
Frequent Itemset Using FP-Growth
(Example)

23. 23
null
A:2 B:1
C:1
C:1
D:1
D:1
E:1
E:1
Conditional Pattern base
for E:
P = {(A:1,C:1,D:1,E:1),
(A:1,D:1,E:1),
(B:1,C:1,E:1)}
Count for E is 3: {E} is
frequent itemset
Recursively apply FP-
growth on P (Conditional
tree for D within
conditional tree for E)
E:1
Conditional tree for E:
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

24. 24
AA BB CC DD EE
AB AC AD AE BC BD BE CD CE DEAB AC AD AE BC BD BE CD CE DE
ABC ABD ABE ACD ACE ADE BCD BCE BDE CDEABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
ABCDABCD ABCEABCE ABDEABDE ACDE BCDEACDE BCDE
ABCDEABCDE
Frequent Itemset Using FP-Growth
(Example)

25. 25
Conditional pattern base
for D within conditional
base for E:
P = {(A:1,C:1,D:1),
(A:1,D:1)}
Count for D is 2: {D,E} is
frequent itemset
Recursively apply FP-
growth on P (Conditional
tree for C within
conditional tree D within
conditional tree for E)
Conditional tree for D
within conditional tree
for E:
null
A:2
C:1
D:1
D:1
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

26. 26
Conditional pattern base
for C within D within E:
P = {(A:1,C:1)}
Count for C is 1: {C,D,E}
is NOT frequent itemset
Recursively apply FP-
growth on P
(Conditional tree for A
within conditional tree D
within conditional tree
for E)
Conditional tree for C
within D within E:
null
A:1
C:1
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

27. 27
Count for A is 2: {A,D,E}
is frequent itemset
Next step:
Construct conditional tree
C within conditional tree
E
Conditional tree for A
within D within E:
null
A:2
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

28. 28
null
A:2 B:1
C:1
C:1
D:1
D:1
E:1
E:1
Recursively apply FP-
growth on P (Conditional
tree for C within
conditional tree for E)
E:1
Conditional tree for E:
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

29. 29
null
A:1 B:1
C:1
C:1
E:1 E:1
FP Growth Algorithm: FP Tree Mining
Conditional pattern base
for C within conditional
base for E:
P = {(B:1,C:1),
(A:1,C:1)}
Count for C is 2: {C,E} is
frequent itemset
Recursively apply FP-
growth on P (Conditional
tree for B within
conditional tree C within
conditional tree for E)Conditional tree for C within conditional
tree for E:
Frequent Itemset Using FP-Growth
(Example)

30. 30
null
A:7
B:5
B:3
C:3
D:1
C:1
D:1
C:3
D:1
D:1
E:1
E:1
TID Items
1 {A,B}
2 {B,C,D}
3 {A,C,D,E}
4 {A,D,E}
5 {A,B,C}
6 {A,B,C,D}
7 {B,C}
8 {A,B,C}
9 {A,B,D}
10 {B,C,E}
D:1
E:1
Transaction
Database
Item Pointer
A
B
C
D
E
Header table
FP Growth Algorithm: FP Tree Mining
Frequent Itemset Using FP-Growth
(Example)

31. 31
AA BB CC DD EE
AB AC AD AE BC BD BE CD CE DEAB AC AD AE BC BD BE CD CE DE
ABC ABD ABE ACD ACE ADE BCD BCE BDE CDEABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
ABCDABCD ABCEABCE ABDEABDE ACDE BCDEACDE BCDE
ABCDEABCDE
Frequent Itemset Using FP-Growth
(Example)

32. 32
AA BB CC DD EE
AB AC AD AE BC BD BE CD CE DEAB AC AD AE BC BD BE CD CE DE
ABC ABD ABE ACD ACE ADE BCD BCE BDE CDEABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
ABCDABCD ABCEABCE ABDEABDE ACDE BCDEACDE BCDE
ABCDEABCDE
Frequent Itemset Using FP-Growth
(Example)