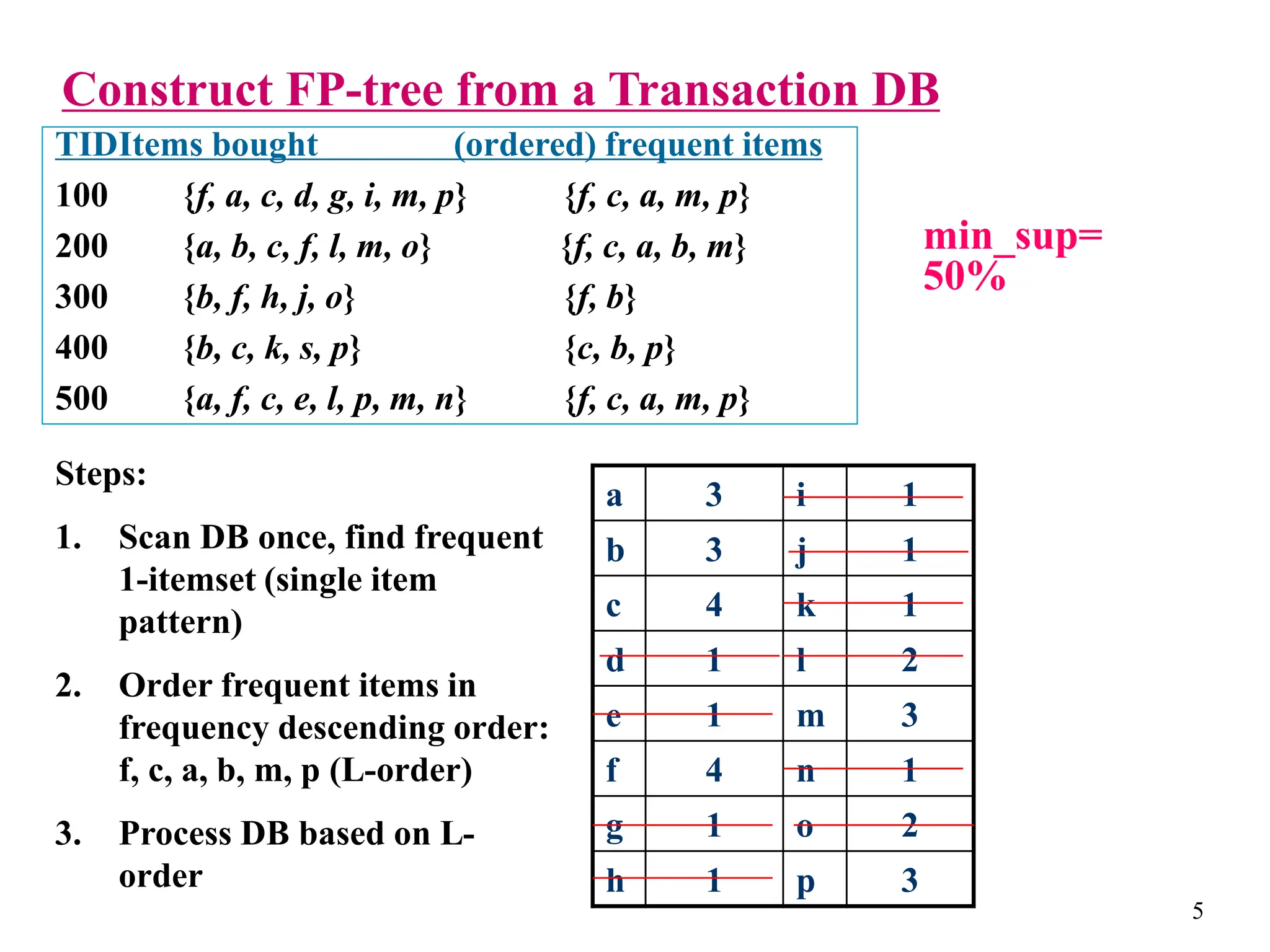
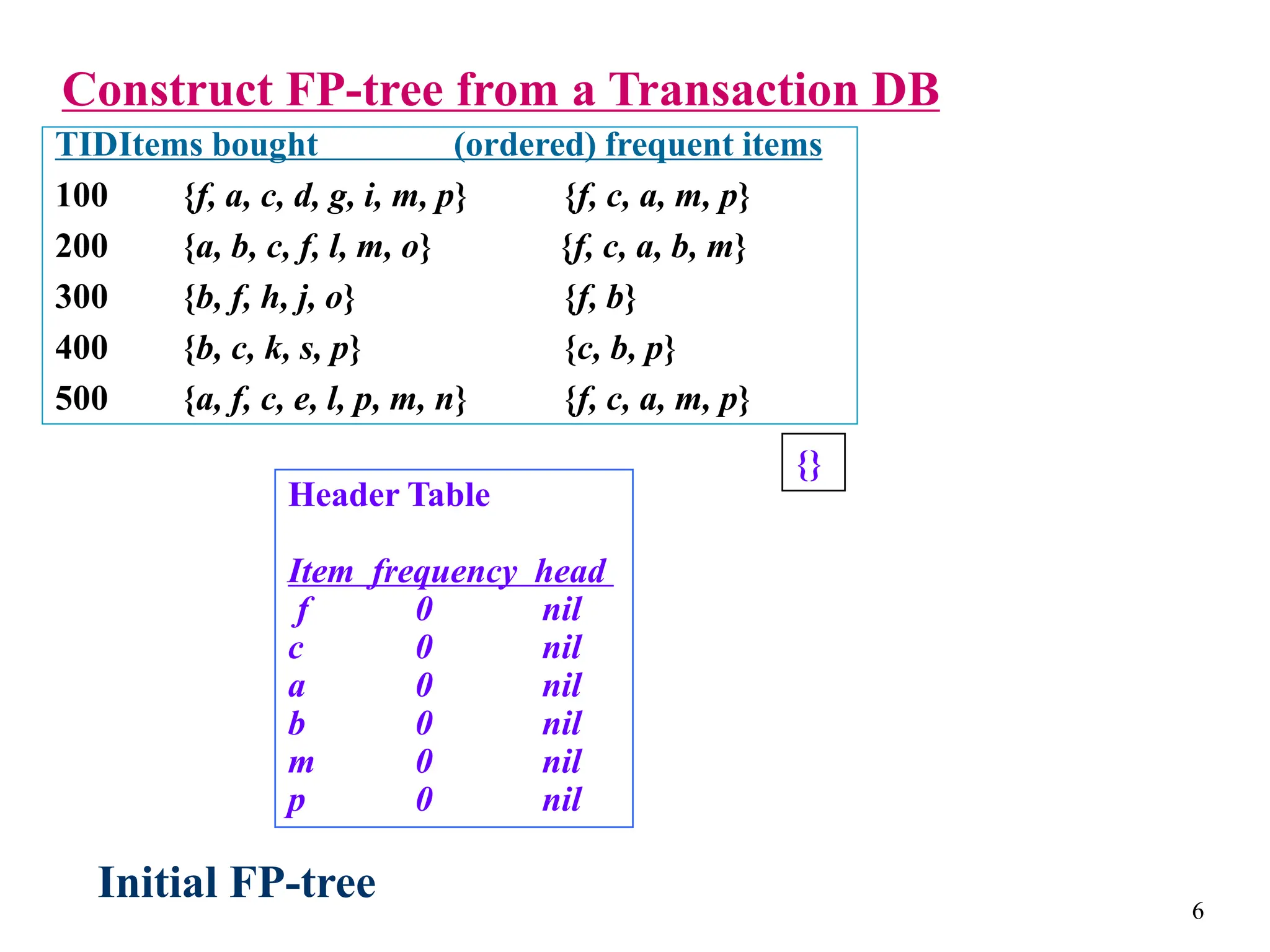
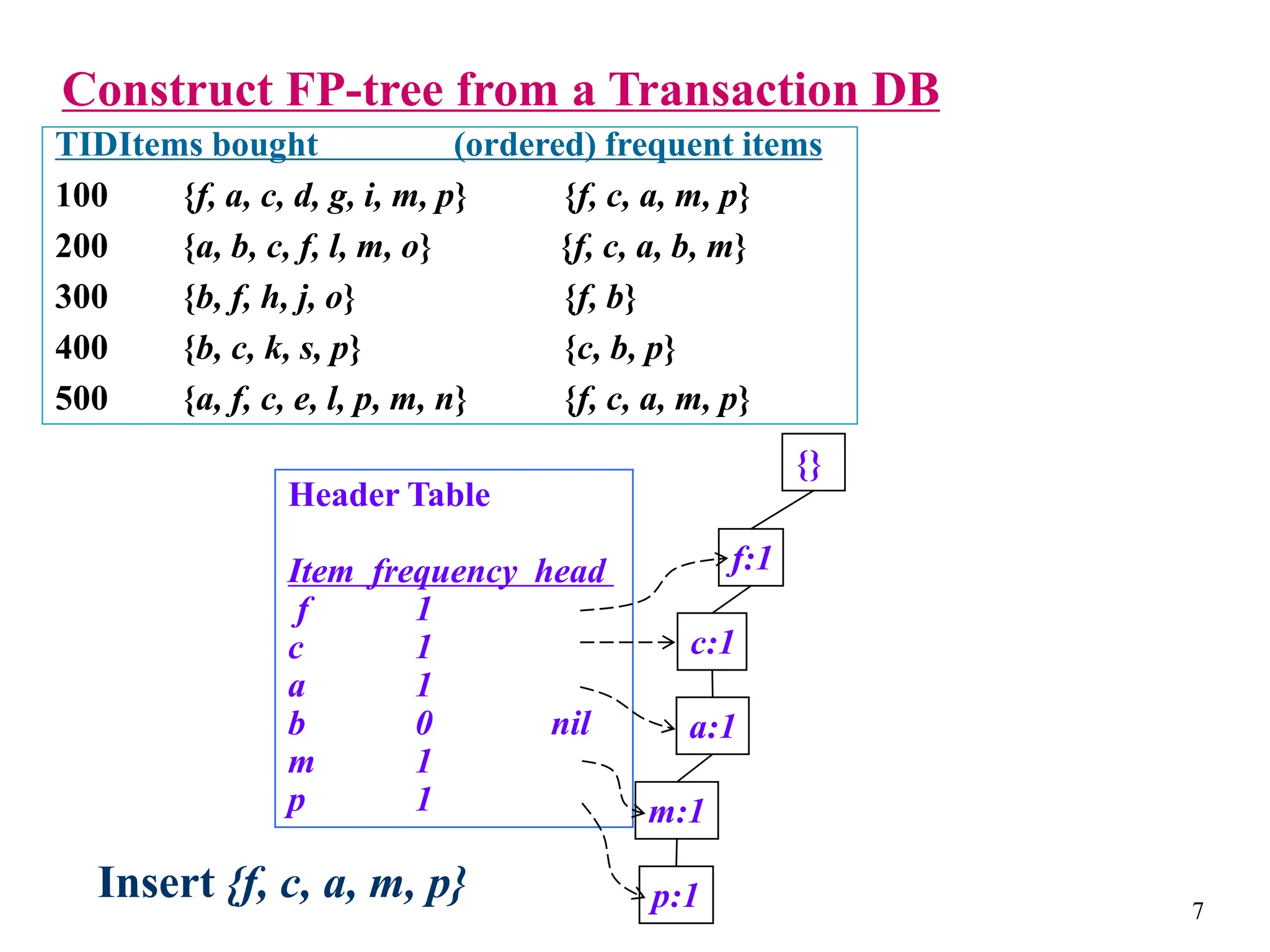
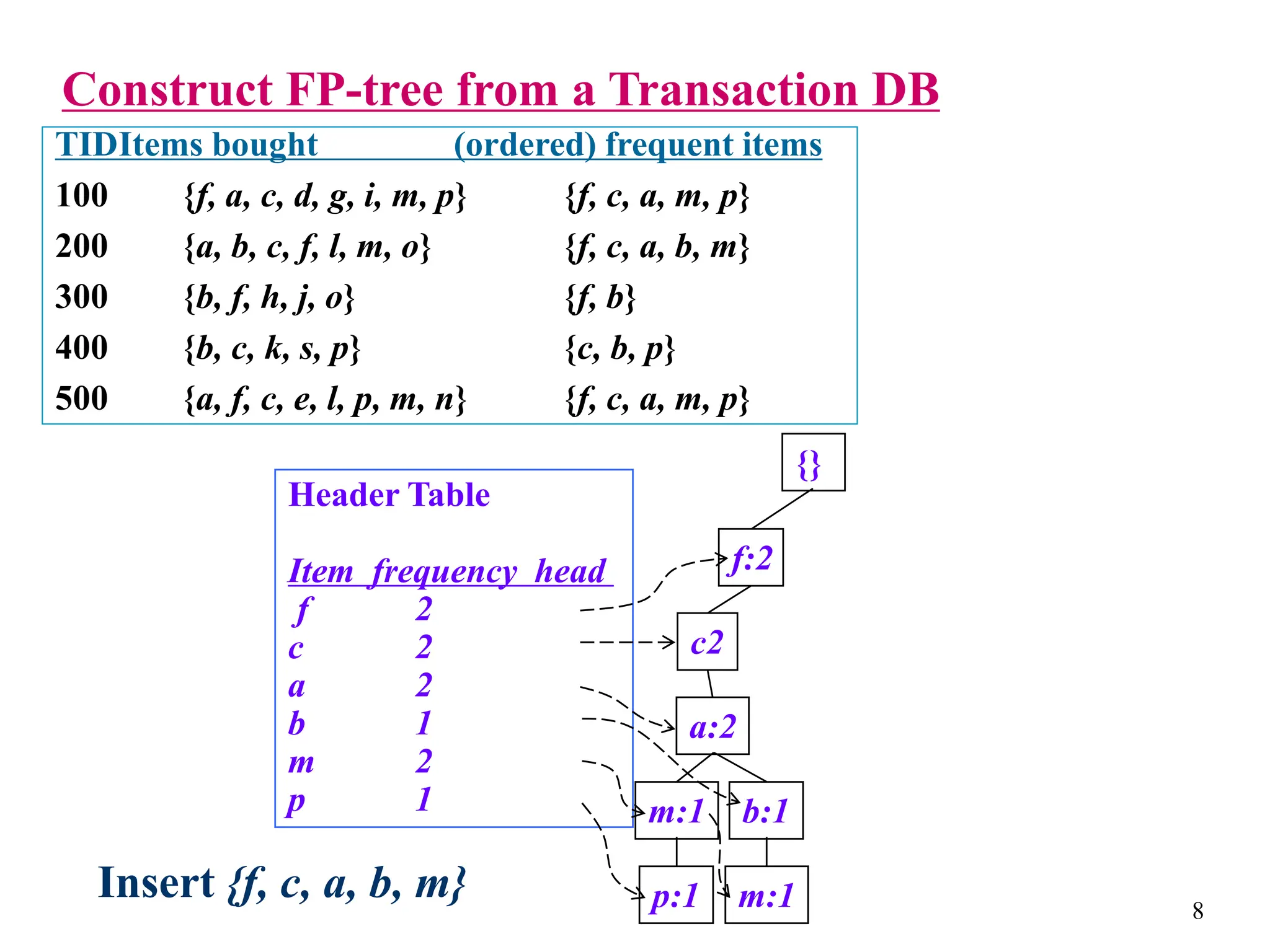
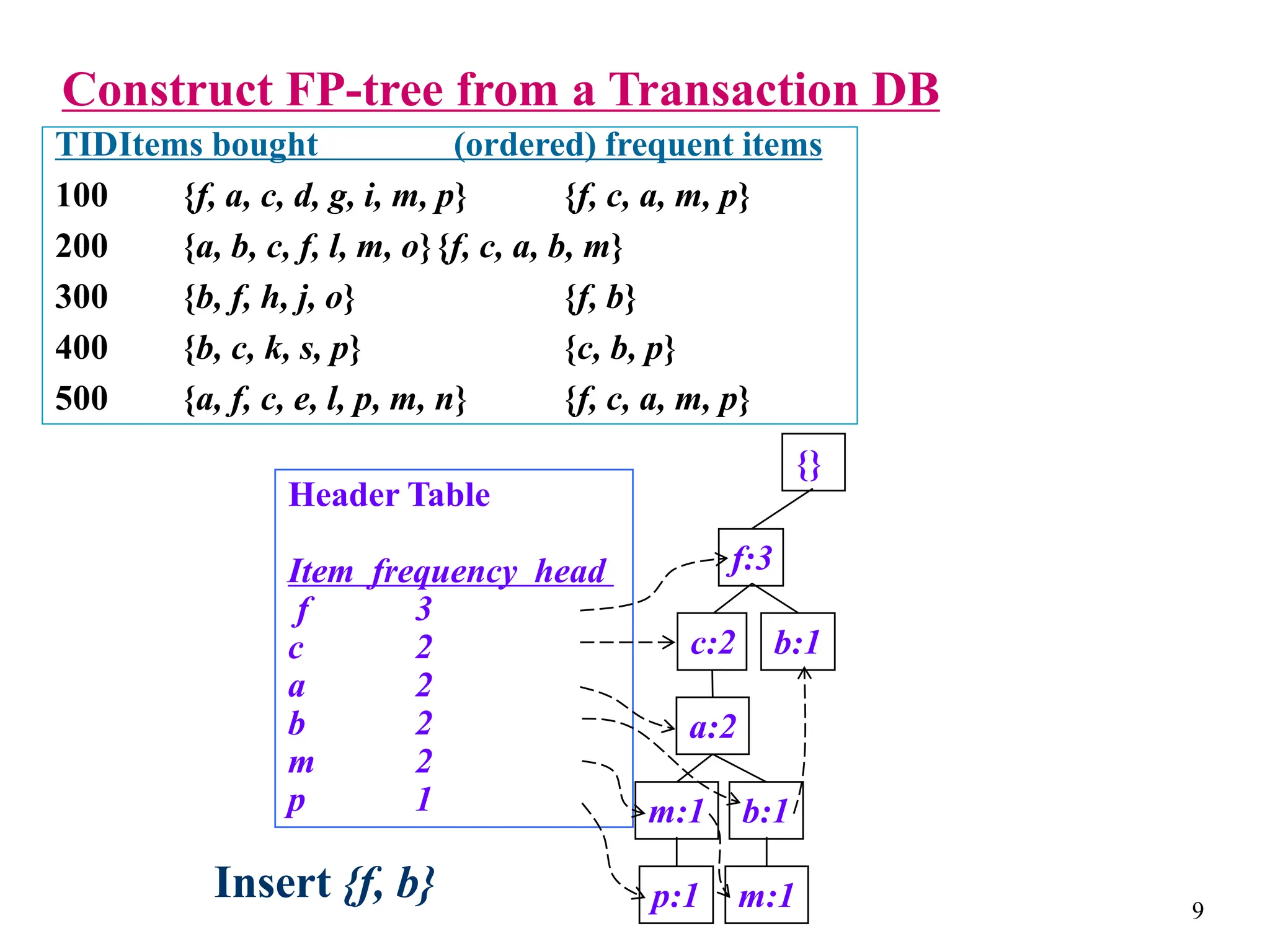
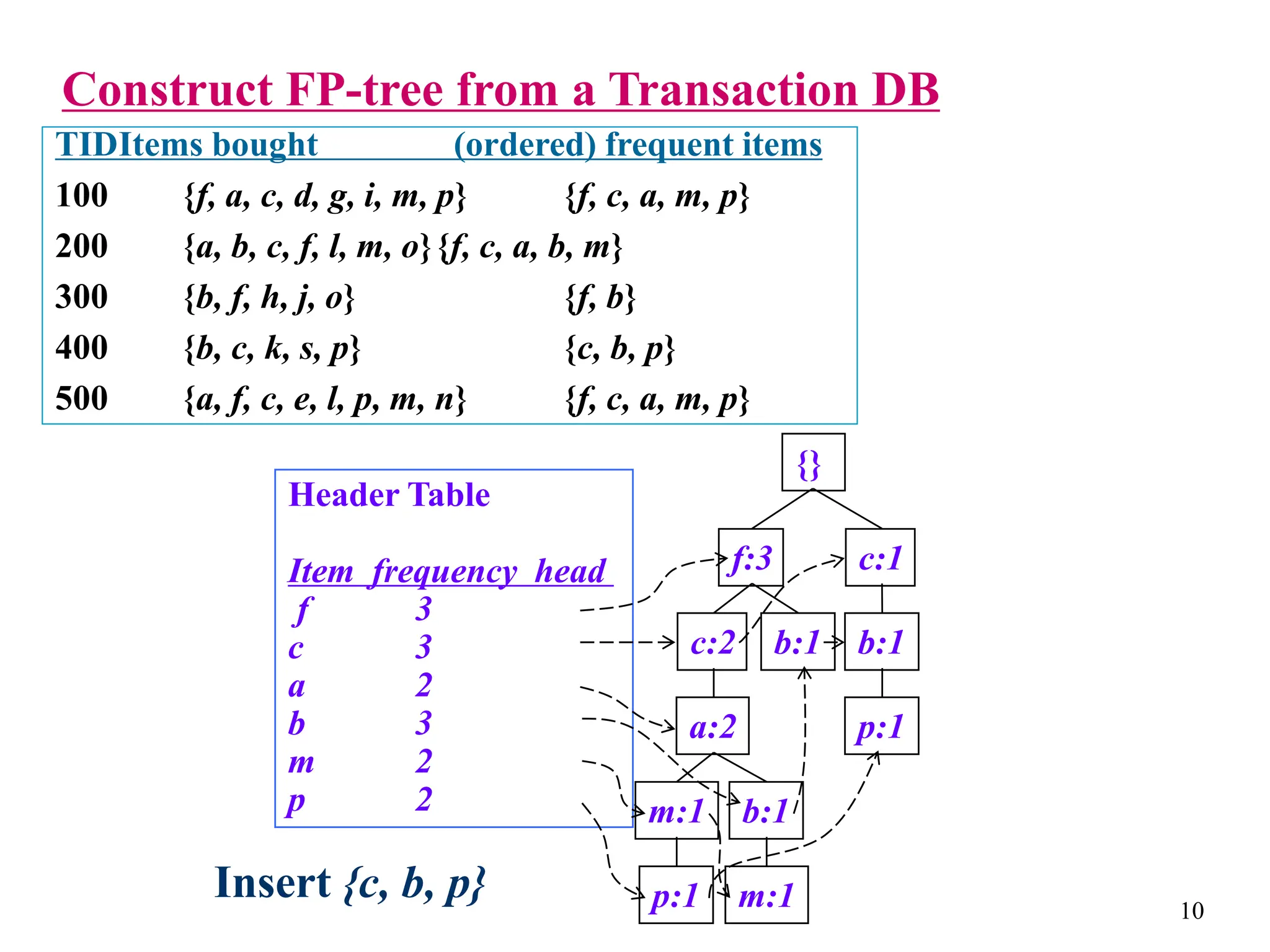
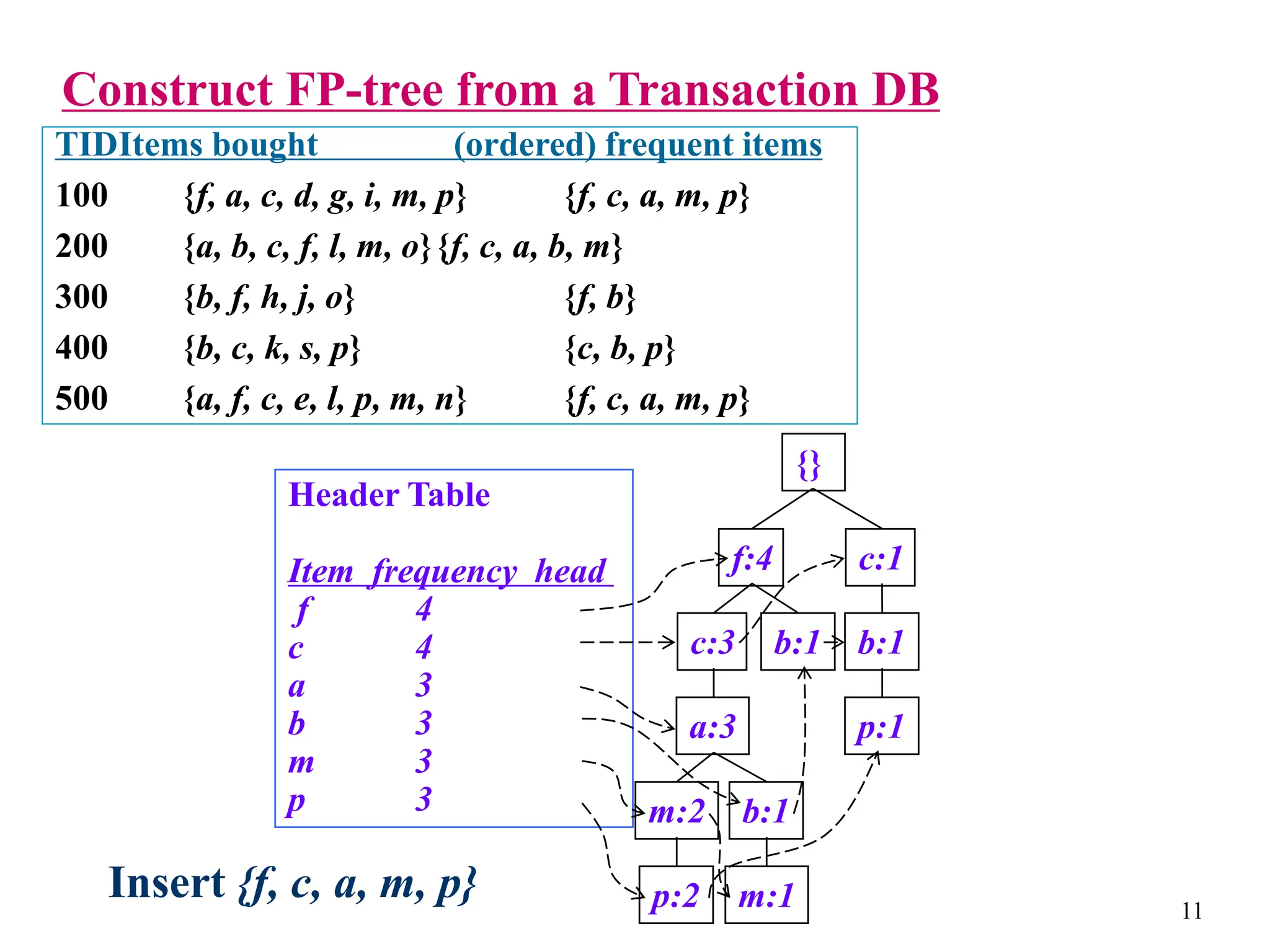
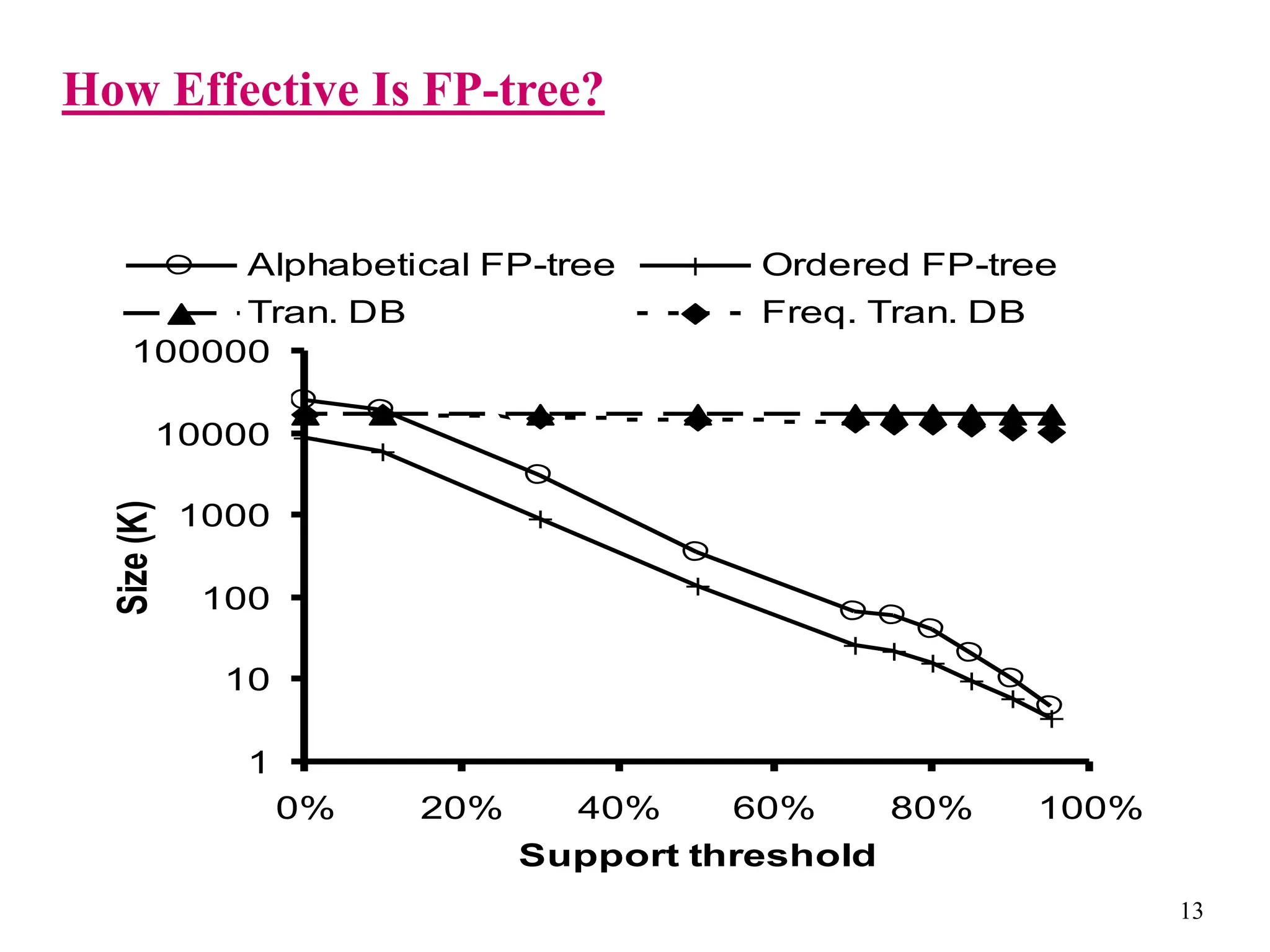
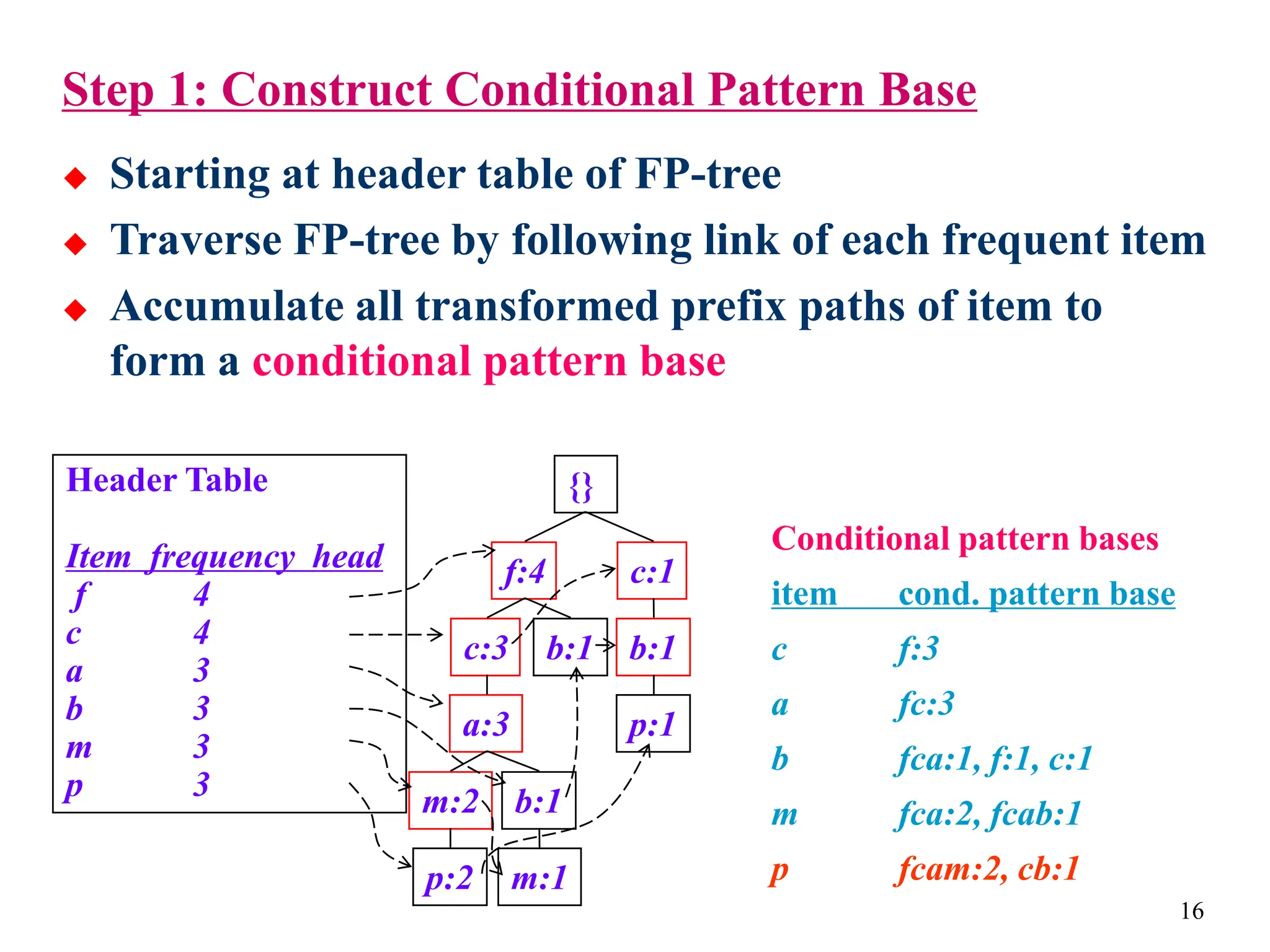
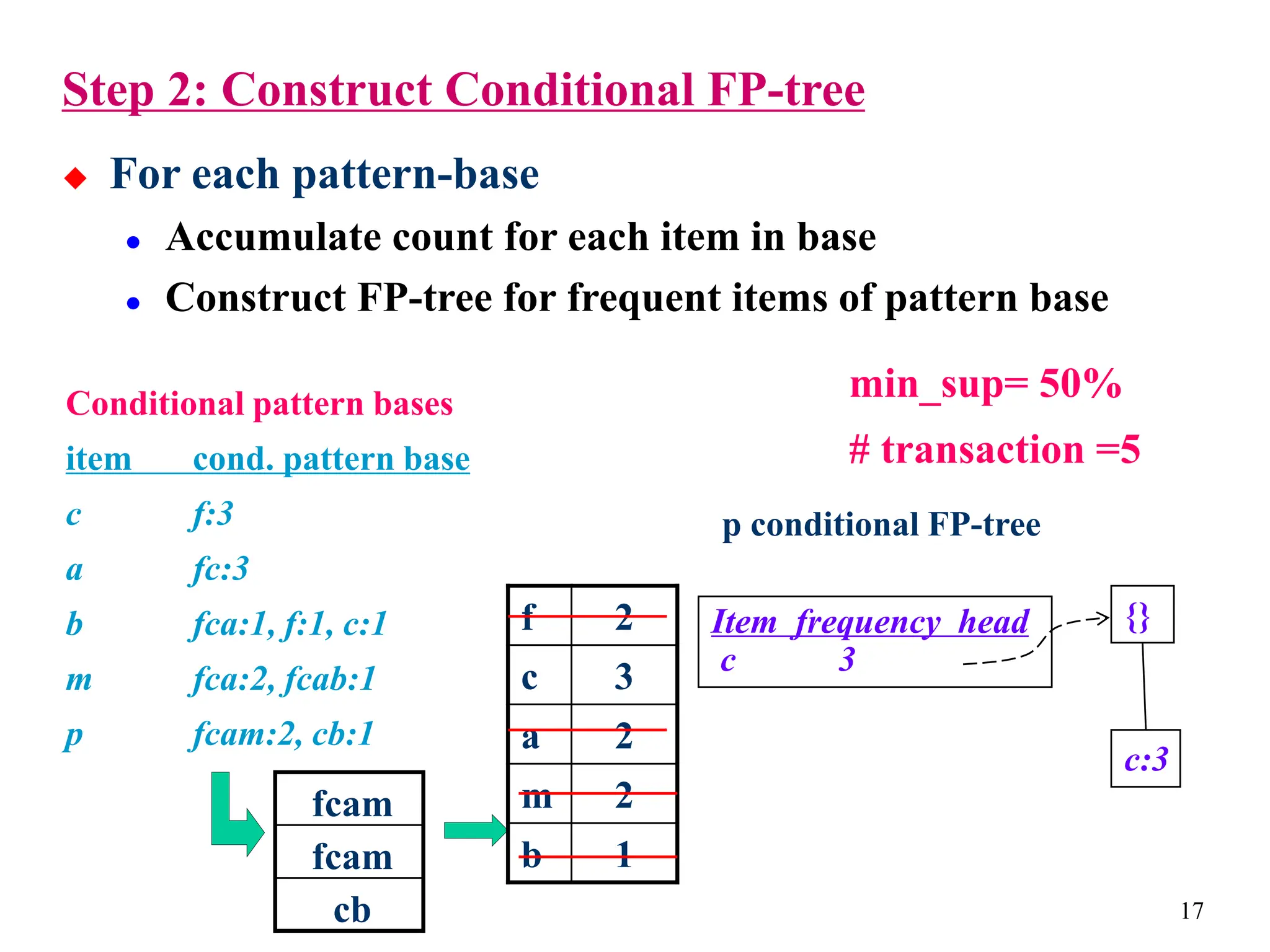
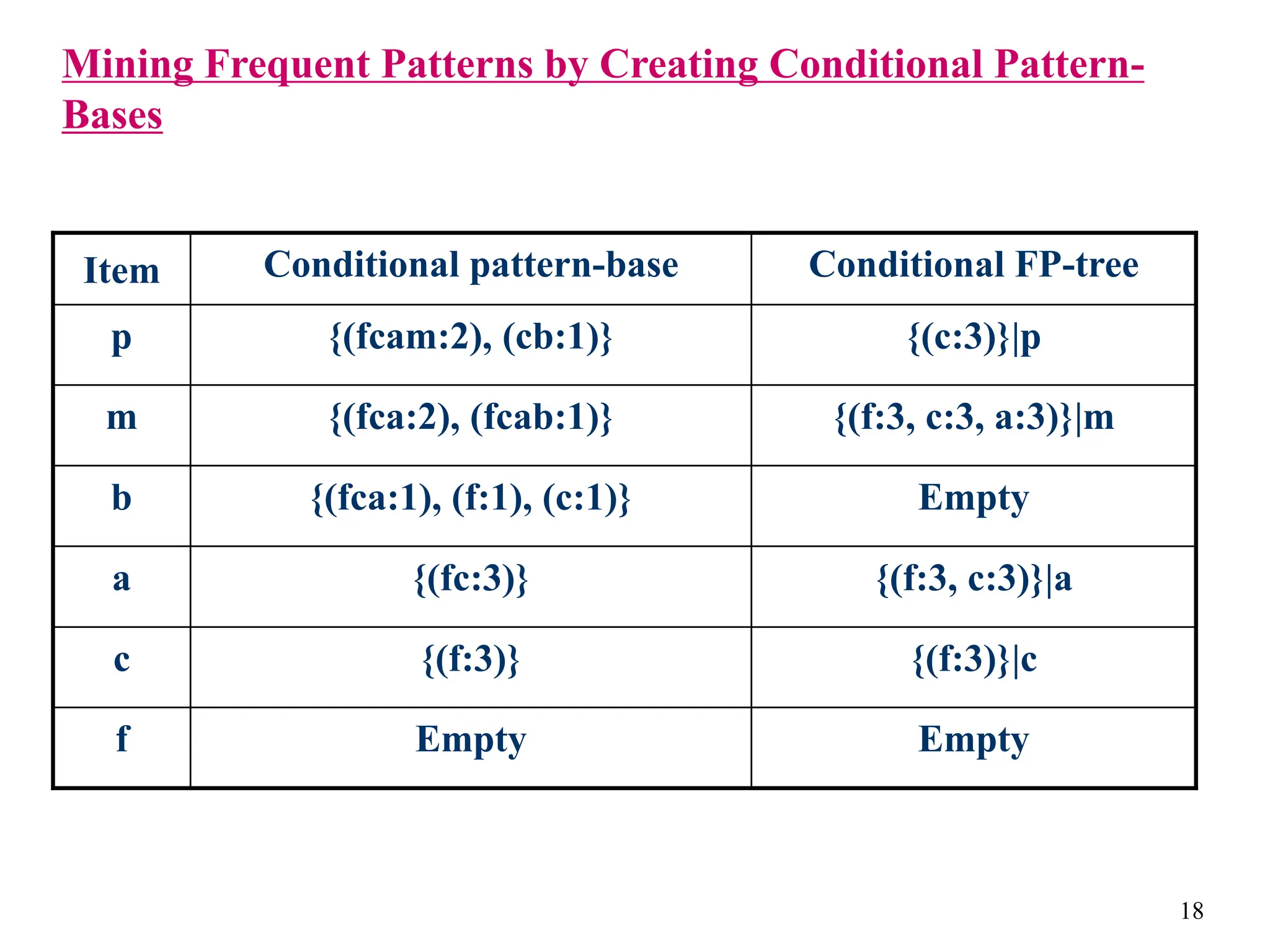
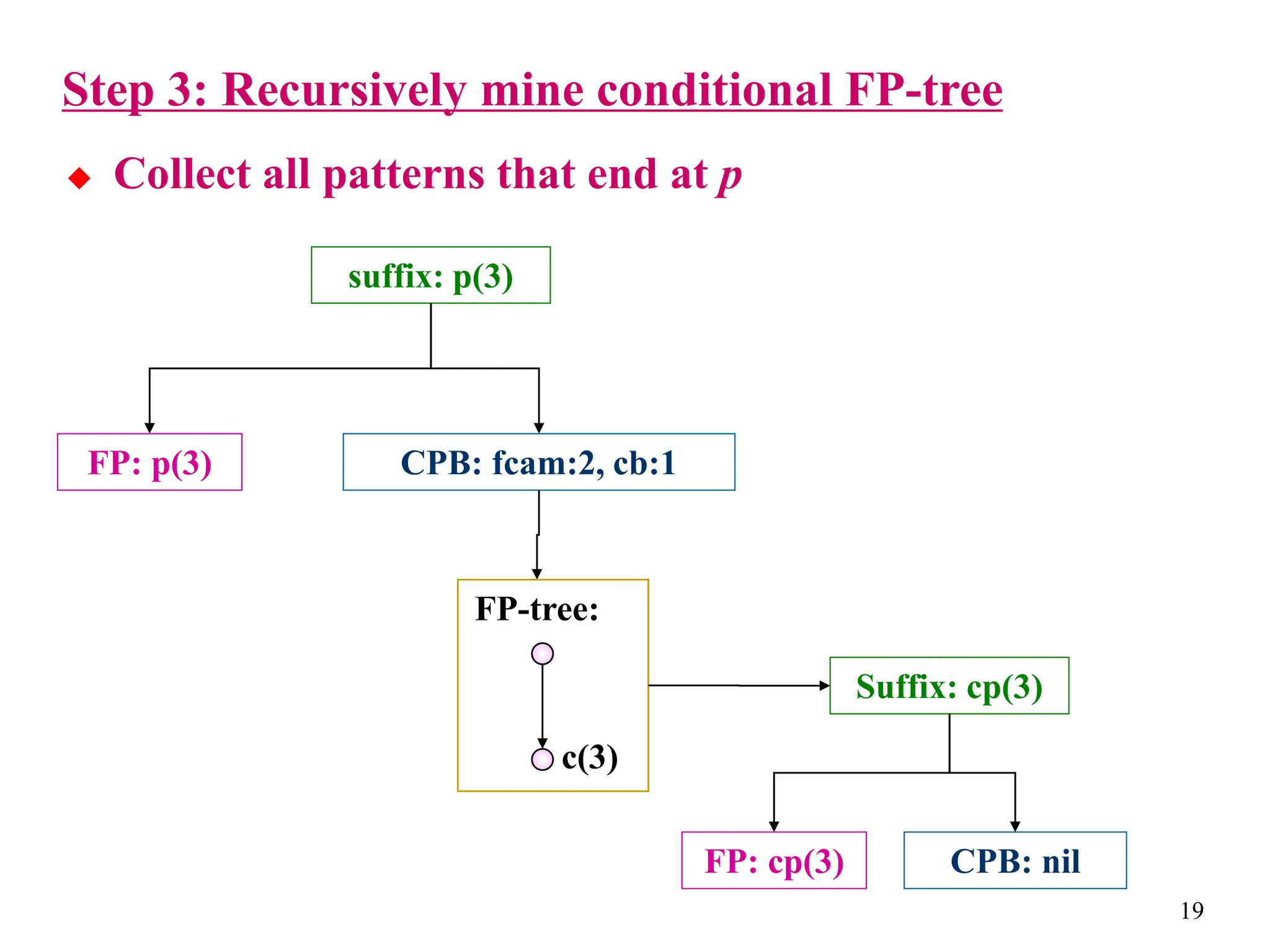
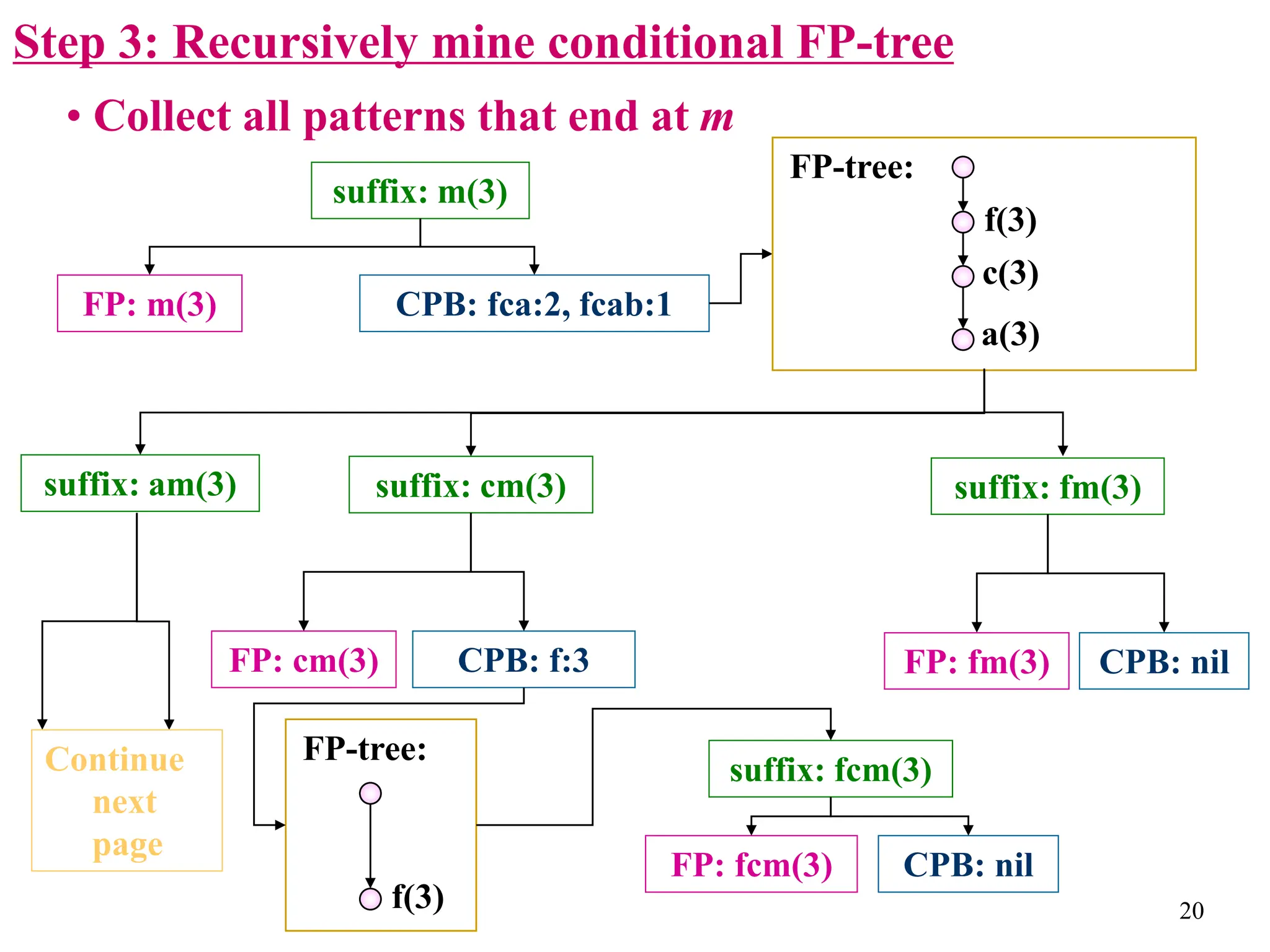
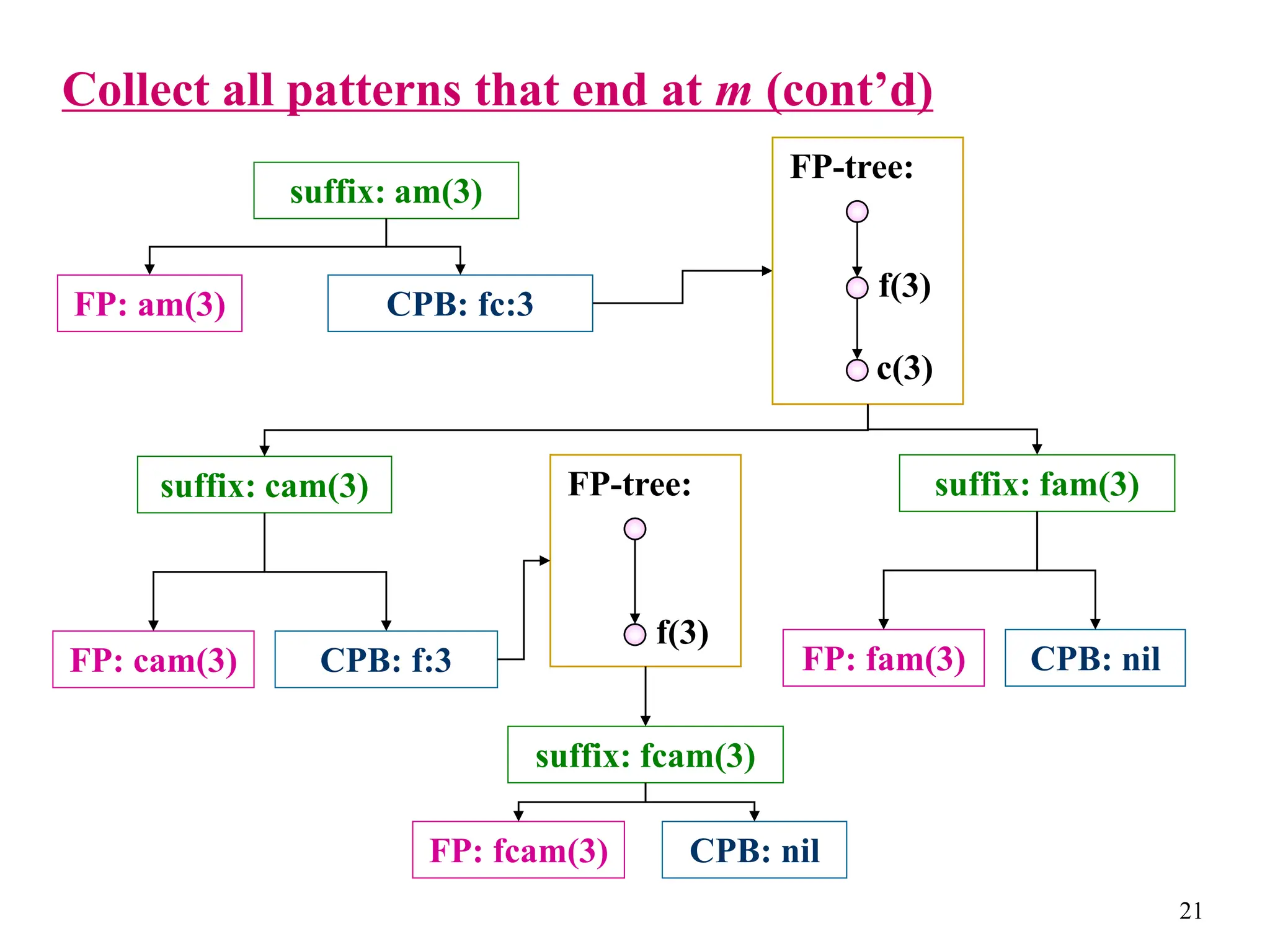
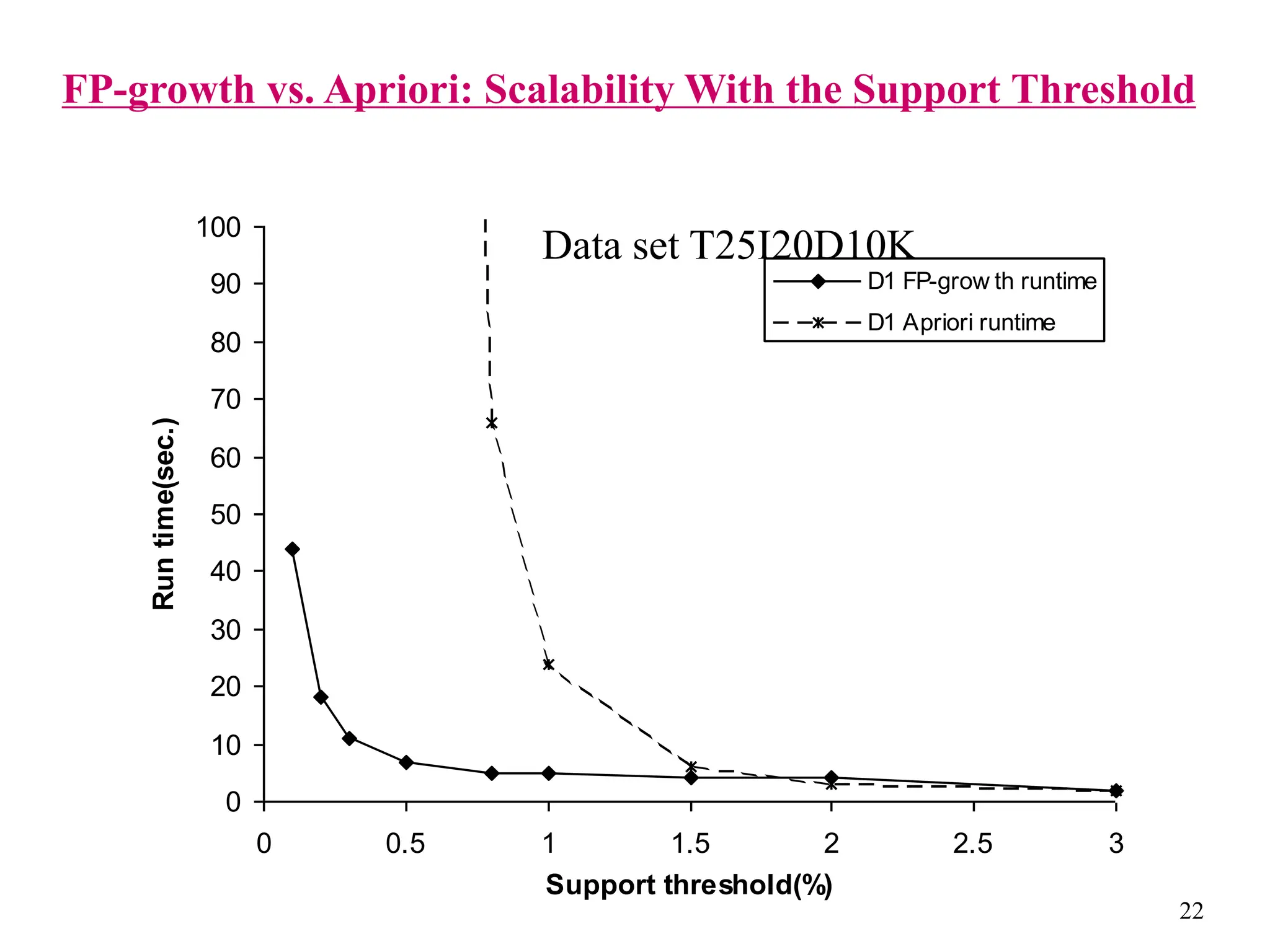
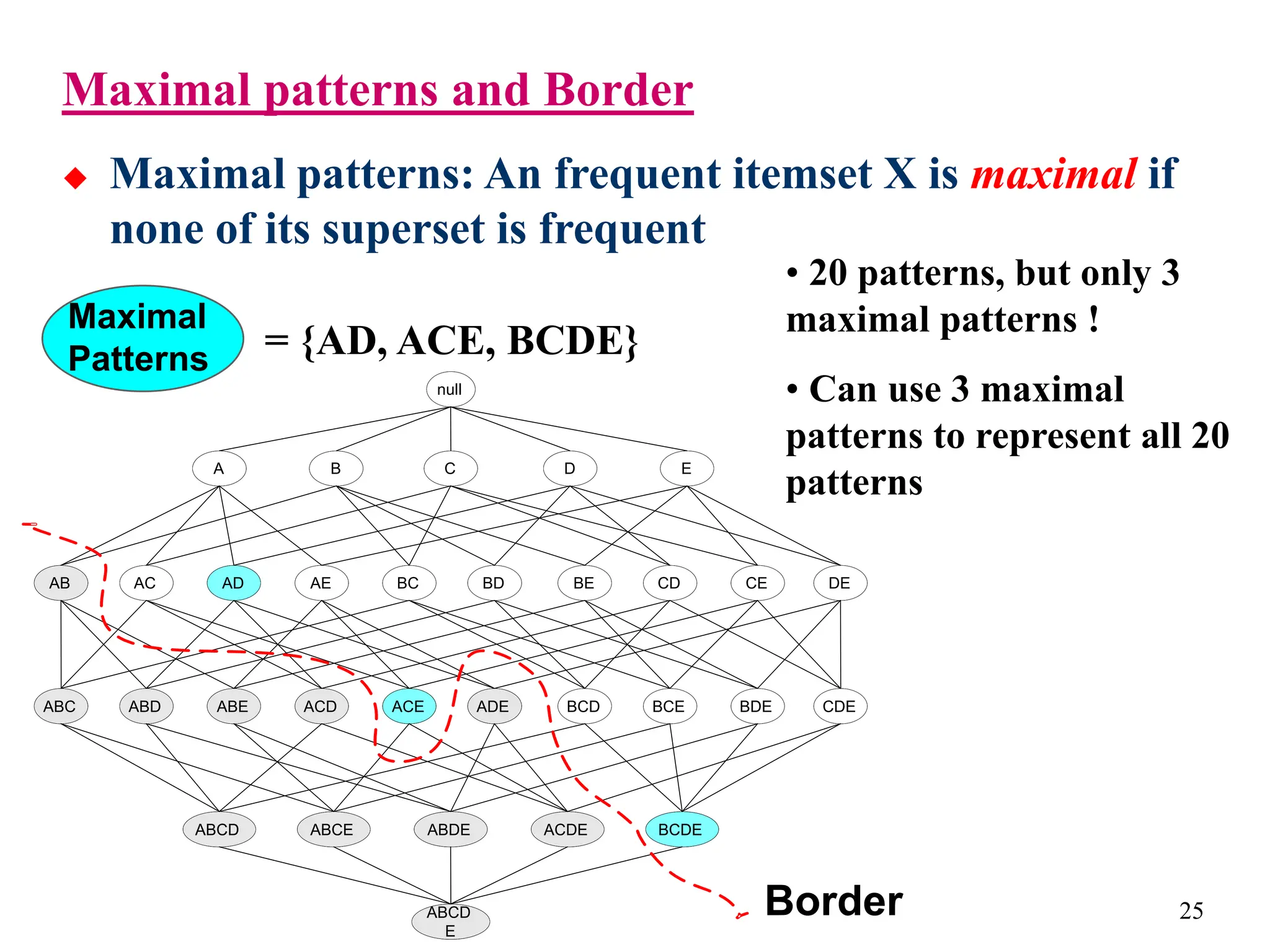
The document discusses the frequent pattern tree (FP-tree) structure for efficiently mining frequent patterns without candidate generation. It describes how an FP-tree compresses a transaction database into a tree structure that preserves all frequent itemsets. The FP-growth algorithm recursively mines the FP-tree to discover all frequent patterns by creating conditional pattern bases and conditional FP-trees. FP-growth avoids multiple database scans and candidate generation, making it faster than the Apriori algorithm. However, it is dependent on support threshold and cannot handle incremental updates.

1. Frequent-Pattern Tree

2. 2
Bottleneck of Frequent-pattern Mining
 Multiple database scans are costly
 Mining long patterns needs many passes of scanning
and generates lots of candidates
 To find frequent itemset i1i2…i100
 # of scans: 100
 # of Candidates: (100
1) + (100
2) + … + (1
1
0
0
0
0) = 2100-1 =
1.27*1030 !
 Bottleneck: candidate-generation-and-test
 Can we avoid candidate generation?

3. 3
 Grow long patterns from short ones using local frequent
items
 “abc” is a frequent pattern
 Get all transactions having “abc”: DB|abc (projected
database on abc)
 “d” is a local frequent item in DB|abc  abcd is a frequent
pattern
 Get all transactions having “abcd” (projected database on
“abcd”) and find longer itemsets
Mining Freq Patterns w/o Candidate Generation

4. 4
Mining Freq Patterns w/o Candidate Generation
 Compress a large database into a compact, Frequent-
Pattern tree (FP-tree) structure
 Highly condensed, but complete for frequent pattern
mining
 Avoid costly database scans
 Develop an efficient, FP-tree-based frequent pattern
mining method
 A divide-and-conquer methodology: decompose mining
tasks into smaller ones
 Avoid candidate generation: examine sub-database
(conditional pattern base) only!

5. 5
Construct FP-tree from a Transaction DB
min_sup=
50%
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Steps:
1. Scan DB once, find frequent
1-itemset (single item
pattern)
2. Order frequent items in
frequency descending order:
f, c, a, b, m, p (L-order)
3. Process DB based on L-
order
a 3 i 1
b 3 j 1
c 4 k 1
d 1 l 2
e 1 m 3
f 4 n 1
g 1 o 2
h 1 p 3

6. 6
Construct FP-tree from a Transaction DB
{}
Header Table
Item frequency head
f 0 nil
c 0 nil
a 0 nil
b 0 nil
m 0 nil
p 0 nil
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Initial FP-tree

7. 7
Construct FP-tree from a Transaction DB
{}
f:1
c:1
a:1
m:1
p:1
Header Table
Item frequency head
f 1
c 1
a 1
b 0 nil
m 1
p 1
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Insert {f, c, a, m, p}

8. 8
Construct FP-tree from a Transaction DB
{}
f:2
c2
a:2
b:1
m:1
p:1 m:1
Header Table
Item frequency head
f 2
c 2
a 2
b 1
m 2
p 1
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Insert {f, c, a, b, m}

9. 9
Construct FP-tree from a Transaction DB
{}
f:3
b:1
c:2
a:2
b:1
m:1
p:1 m:1
Header Table
Item frequency head
f 3
c 2
a 2
b 2
m 2
p 1
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o}{f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Insert {f, b}

10. 10
Construct FP-tree from a Transaction DB
{}
f:3 c:1
b:1
p:1
b:1
c:2
a:2
b:1
m:1
p:1 m:1
Header Table
Item frequency head
f 3
c 3
a 2
b 3
m 2
p 2
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o}{f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Insert {c, b, p}

11. 11
Construct FP-tree from a Transaction DB
{}
f:4 c:1
b:1
p:1
b:1
c:3
a:3
b:1
m:2
p:2 m:1
Header Table
Item frequency head
f 4
c 4
a 3
b 3
m 3
p 3
TIDItems bought (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o}{f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}
Insert {f, c, a, m, p}

12. 12
Benefits of FP-tree Structure
 Completeness:
 Preserve complete DB information for frequent pattern
mining (given prior min support)
 Each transaction mapped to one FP-tree path; counts
stored at each node
 Compactness
 One FP-tree path may correspond to multiple
transactions; tree is never larger than original database
(if not count node-links and counts)
 Reduce irrelevant information—infrequent items are
gone
 Frequency-descending ordering: more frequent items are
closer to tree top and more likely to be shared

13. 13
How Effective Is FP-tree?
1
10
100
1000
10000
100000
0% 20% 40% 60% 80% 100%
Support threshold
Size
(K)
Alphabetical FP-tree Ordered FP-tree
Tran. DB Freq. Tran. DB
Dataset: Connect-4
(a dense dataset)

14. 14
Mining Frequent Patterns Using FP-tree
 General idea (divide-and-conquer)
 Recursively grow frequent pattern path using FP-tree
 Frequent patterns can be partitioned into subsets
according to L-order
 L-order=f-c-a-b-m-p
 Patterns containing p
 Patterns having m but no p
 Patterns having b but no m or p
 …
 Patterns having c but no a nor b, m, p
 Pattern f

15. 15
Mining Frequent Patterns Using FP-tree
 Step 1 : Construct conditional pattern base for each
item in header table
 Step 2: Construct conditional FP-tree from each
conditional pattern-base
 Step 3: Recursively mine conditional FP-trees and grow
frequent patterns obtained so far
 If conditional FP-tree contains a single path, simply
enumerate all patterns

16. 16
Step 1: Construct Conditional Pattern Base
 Starting at header table of FP-tree
 Traverse FP-tree by following link of each frequent item
 Accumulate all transformed prefix paths of item to
form a conditional pattern base
Conditional pattern bases
item cond. pattern base
c f:3
a fc:3
b fca:1, f:1, c:1
m fca:2, fcab:1
p fcam:2, cb:1
{}
f:4 c:1
b:1
p:1
b:1
c:3
a:3
b:1
m:2
p:2 m:1
Header Table
Item frequency head
f 4
c 4
a 3
b 3
m 3
p 3

17. 17
Step 2: Construct Conditional FP-tree
 For each pattern-base
 Accumulate count for each item in base
 Construct FP-tree for frequent items of pattern base
Conditional pattern bases
item cond. pattern base
c f:3
a fc:3
b fca:1, f:1, c:1
m fca:2, fcab:1
p fcam:2, cb:1
p conditional FP-tree
f 2
c 3
a 2
m 2
b 1
{}
c:3
Item frequency head
c 3
min_sup= 50%
# transaction =5
fcam
fcam
cb

18. 18
Mining Frequent Patterns by Creating Conditional Pattern-
Bases
Empty
Empty
f
{(f:3)}|c
{(f:3)}
c
{(f:3, c:3)}|a
{(fc:3)}
a
Empty
{(fca:1), (f:1), (c:1)}
b
{(f:3, c:3, a:3)}|m
{(fca:2), (fcab:1)}
m
{(c:3)}|p
{(fcam:2), (cb:1)}
p
Conditional FP-tree
Conditional pattern-base
Item

19. 19
Step 3: Recursively mine conditional FP-tree
suffix: p(3)
FP: p(3) CPB: fcam:2, cb:1
c(3)
FP-tree:
Suffix: cp(3)
FP: cp(3) CPB: nil
 Collect all patterns that end at p

20. 20
• Collect all patterns that end at m
suffix: m(3)
FP: m(3) CPB: fca:2, fcab:1
suffix: cm(3)
FP: cm(3) CPB: f:3
f(3)
FP-tree:
c(3)
suffix: fm(3)
FP: fm(3) CPB: nil
f(3)
FP-tree:
suffix: fcm(3)
FP: fcm(3) CPB: nil
a(3)
suffix: am(3)
Continue
next
page
Step 3: Recursively mine conditional FP-tree

21. 21
Collect all patterns that end at m (cont’d)
suffix: am(3)
FP: am(3) CPB: fc:3
suffix: cam(3)
FP: cam(3) CPB: f:3
f(3)
FP-tree:
c(3)
suffix: fam(3)
FP: fam(3) CPB: nil
f(3)
FP-tree:
suffix: fcam(3)
FP: fcam(3) CPB: nil

22. 22
FP-growth vs. Apriori: Scalability With the Support Threshold
0
10
20
30
40
50
60
70
80
90
100
0 0.5 1 1.5 2 2.5 3
Support threshold(%)
Run
time(sec.)
D1 FP-grow th runtime
D1 Apriori runtime
Data set T25I20D10K

23. 23
Why Is Frequent Pattern Growth Fast?
 Performance study shows
 FP-growth is an order of magnitude faster than Apriori
 Reasoning
 No candidate generation, no candidate test
 Use compact data structure
 Eliminate repeated database scan
 Basic operations are counting and FP-tree building

24. 24
Weaknesses of FP-growth
 Support dependent; cannot accommodate dynamic
support threshold
 Cannot accommodate incremental DB update
 Mining requires recursive operations

25. 25
Maximal patterns and Border
 Maximal patterns: An frequent itemset X is maximal if
none of its superset is frequent
Maximal
Patterns
null
AB AC AD AE BC BD BE CD CE DE
A B C D E
ABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
ABCD ABCE ABDE ACDE BCDE
ABCD
E
Border
= {AD, ACE, BCDE}
• 20 patterns, but only 3
maximal patterns !
• Can use 3 maximal
patterns to represent all 20
patterns

26. 26
Closed Itemsets
 An itemset X is closed if there exists no item y
(yX) such that every transaction containing X
also contains y
Tid Itemset
1 ACTW
2 CDW
3 ACTW
4 ACDW
5 ACDTW
6 CDT
Example:
• AC is not closed since every
transaction containing AC also
contains W
• CDW is closed since
transaction Tid=2 contains no
other item

27. 27
Frequent Closed Patterns
 For frequent itemset X, if there exists no item y s.t.
every transaction containing X also contains y, then X is
a frequent closed pattern
 “acdf” is a frequent closed pattern
 Concise rep. of freq pats
 Reduce # of patterns and rules
 N. Pasquier et al. In ICDT’99
TID Items
10 a, c, d, e, f
20 a, b, e
30 c, e, f
40 a, c, d, f
50 c, e, f
Min_sup=2