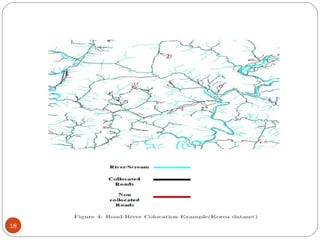
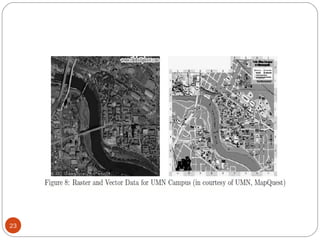
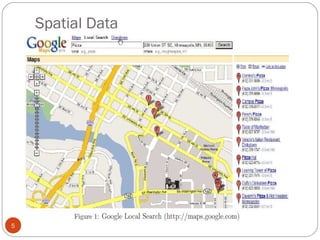
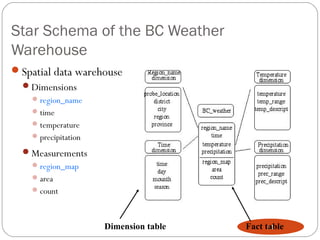
This document discusses spatial data mining and its applications. Spatial data mining involves extracting knowledge and relationships from large spatial databases. It can be used for applications like GIS, remote sensing, medical imaging, and more. Some challenges include the complexity of spatial data types and large data volumes. The document also covers topics like spatial data warehouses, dimensions and measures in spatial analysis, spatial association rule mining, and applications in fields such as earth science, crime mapping, and commerce.

1. 1
Spatial Data Mining

2. Spatial Database
2
Stores a large amount of space-related data
Maps
Remote Sensing
Medical Imaging
VLSI chip layout
Have Topological and distance information
Require spatial indexing, data access, reasoning ,geometric
computation and knowledge representation techniques

3. Spatial Data Mining
3
Extraction of knowledge, spatial relationships from
spatial databases
Can be used for understanding spatial data and spatial
relationships
Applications:
GIS, Geomarketing, Remote Sensing, Image database
exploration, medical imaging, Navigation
Challenges
Complexity of spatial data types and access methods
Large amounts of data

4. Cont.
4
Non-spatial Information
Same as data in traditional data mining
Numerical, categorical, ordinal, boolean, etc
e.g., city name, city population
Spatial Information
Spatial attribute: geographically referenced
 Neighborhood and extent
Location, e.g., longitude, latitude, elevation
Spatial data representations
Raster: gridded space
Vector: point, line, polygon
Graph: node, edge, path

5. Spatial Data
5

6. Cont.
6

7. Statistical techniques
7
Popular approach to analyze spatial data
Assumes independence among spatial data
Can be performed only by experts
Do not work well with symbolic values

8. Spatial Data Warehousing
8
Spatial data warehouse: Integrated, subject-oriented, time-variant,
and nonvolatile spatial data repository.
It consists of both spatial and non spatial in support of spatial data mining
and spatial-data-related decision-making processes.
Spatial data cube: multidimensional spatial database
Both dimensions and measures may contain spatial components.
Challenging issues:
Spatial data integration: a big issue
Structure-specific formats (raster- vs. vector-based, OO vs. relational models,
different storage and indexing, etc.)
Vendor-specific formats (ESRI, MapInfo, Intergraph, IDRISI, etc.)
Realization of Fast and flexible OLAP in spatial data warehouses.

9. Dimensions and Measures in Spatial
Data Warehouse
9
Dimensions
non-spatial
e.g. “25-30 degrees” generalizes to“hot” (both are strings)
spatial-to-non spatial
e.g. Seattle generalizes to description “Pacific Northwest” (as a string)
spatial-to-spatial
e.g. Seattle generalizes to Pacific Northwest (as a spatial region)
Measures
numerical (e.g. monthly revenue of a region)
distributive (e.g. count, sum)
algebraic (e.g. average)
holistic (e.g. median, rank)
spatial
collection of spatial pointers (e.g. pointers to all regions with temperature of
25-30 degrees in July)

10. Example: British Columbia Weather
Pattern Analysis
10
Input
A map with about 3,000 weather probes scattered in B.C.
Recording daily data for temperature, precipitation, wind velocity, etc. for a designated
small area and transmitting signal to a provincial weather station.
Data warehouse using star schema
Output
A map that reveals patterns: merged (similar) regions
Goals
Interactive analysis (drill-down, slice, dice, pivot, roll-up)
Fast response time
Minimizing storage space used
Challenge
A merged region may contain hundreds of “primitive” regions (polygons)

11. Star Schema of the BC Weather
Warehouse
Spatial data warehouse
Dimensions
region_name
time
temperature
precipitation
Measurements
region_map
area
count
11Fact tableDimension table

12. 12
Can we precompute all of the possible spatial merges
and store them in the corresponding cuboid cells of a
spatial data cube?
Probably not.
It requires multi-megabytes of storage.
On-line computation is slow and expensive.

13. Dynamic Merging of Spatial
Objects
13

14. Methods for Computing Spatial Data
Cubes
14
On-line aggregation: collect and store pointers to spatial
objects in a spatial data cube
expensive and slow, need efficient aggregation techniques
Precompute and store all the possible combinations
huge space overhead
Precompute and store rough approximations in a spatial data
cube
accuracy trade-off, MBR
Selective computation: only materialize those which will be
accessed frequently
a reasonable choice

15. Mining Spatial Association and
Co-location Patterns
15
Spatial association rule: A ⇒ B [s%, c%]
A and B are sets of spatial or non-spatial predicates
Topological relations: intersects, overlaps, disjoint, etc.
Spatial orientations: left_of, west_of, under, etc.
Distance information: close_to, within_distance, etc.
s% is the support and c% is the confidence of the rule
Examples
is_a(x, “School”) ^ Close_to(x, “Sports_Center”) → close_to(x, “Park”)
[7%, 85%]

16. Progressive Refinement
16
Progressive Refinement:
spatial association mining needs to evaluate multiple spatial relationships
among a large no. of spatial object – expensive.
Hierarchy of spatial relationship:
First search for rough relationship and then refine it
Superset coverage property – all the potential answers should be perserved
(i.e.false-positive test).
Two-step mining of spatial association:
Step 1: Rough spatial computation (as a filter)
 Using MBR for rough estimation
Step2: Detailed spatial algorithm (as refinement)
 Apply only to those objects which have passed the rough spatial association test
(no less than min_support)

17. Spatial co-locations
17
Just what one really wants to explore.
Based on the property of spatial autocorrelation, interesting
features likely coexist in closely located regions.
Efficient methods - Apriori , progressive refinement,etc.

18. 18

19. Spatial Cluster Analysis
19
• Mining clusters—k-means, k-medoids, hierarchical, density-based,
etc.
• Analysis of distinct features of the clusters

20. Spatial Classification
20
Analyze spatial objects to derive classification schemes, such
as decision trees, in relevance to certain spatial properties
(district, highway, river, etc.)
Classifying medium-size families according to income, region, and infant mortality
rates
Mining for volcanoes on Venus
Employ methods such as:
Decision-tree classification, Naïve-Bayesian classifier + boosting, neural network,
genetic programming, etc.

21. Spatial Trend Analysis
21
Function
Detect changes and trends along a spatial dimension
Study the trend of non-spatial or spatial data changing with space
Application examples
Observe the trend of changes of the climate or vegetation with
increasing distance from an ocean
Crime rate or unemployment rate change with regard to city geo-
distribution.
Traffic flows in highways and in cities.

22. Mining Raster Databases
22
Vector data Mining
Maps
Graphs
Molecular chains
Raster data mining
Satellite Images

23. 23

24. Other Applications
24
Spatial data mining is used in
 NASA Earth Observing System (EOS): Earth science data
National Inst. of Justice: crime mapping
 Census Bureau, Dept. of Commerce: census data
 Dept. of Transportation (DOT): traffic data
National Inst. of Health(NIH): cancer clusters
 Commerce, e.g. Retail Analysis