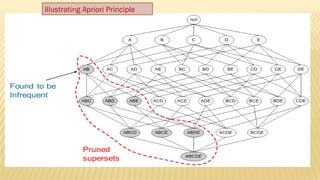
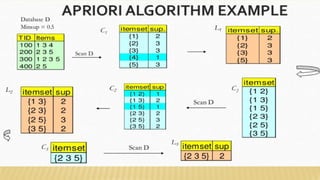
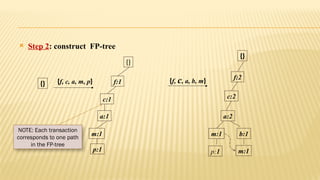
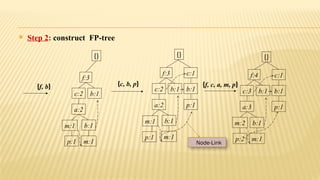
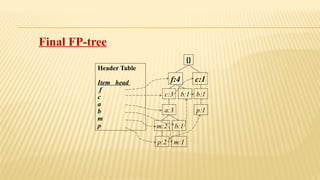
The document presents an improvised apriori algorithm utilizing a frequent pattern tree for association rule mining, focusing on identifying rules that can predict item occurrences within market-basket transactions. It explains key concepts such as itemsets, support count, and the apriori principle, detailing how the algorithm minimizes candidate itemsets through pruning. Additionally, it describes the FP-growth method for efficiently mining frequent patterns from a database, highlighting its two-scan process to build a compact FP-tree structure.

1. IMPROVISED APRIORI
ALGORITHM USING FREQUENT
PATTERN TREE
Supervised By
Dr. Israa Hadi
Presented By
Sura khalid

2. ASSOCIATION RULE

Association Rule mining: Given a set of transactions, find rules that
will predict the occurrence of an item based on the occurrences of
other items in the transaction.
Market-Basket transactions
TID Items
1 Bread, Milk
2 Bread, Diaper, Beer, Eggs
3 Milk, Diaper, Beer, Coke
4 Bread, Milk, Diaper, Beer
5 Bread, Milk, Diaper, Coke
Example of Association Rules
{
Diaper
}
 {Beer},
{Milk, Bread}  {Eggs,Coke},
{Beer, Bread}  {Milk}
,

3. 
key concepts
Itemset
◦
A collection of one or more items
◦
Example: {Milk, Bread, Diaper}
◦
k-itemset
◦
An itemset that contains k items
Support count ()
◦
Frequency of occurrence of an itemset
◦
E.g. ({Milk, Bread,Diaper}) = 2
TID Items
1 Bread, Milk
2 Bread, Diaper, Beer, Eggs
3 Milk, Diaper, Beer, Coke
4 Bread, Milk, Diaper, Beer
5 Bread, Milk, Diaper, Coke

4. RULE EVALUATION METRICS
 Association Rule

An implication expression of the form X  Y, where X and Y are itemsets
*
Support (s)
Fraction of transactions that contain both X and Y
*
Confidence (c)
Measures how often items in Y appear in transactions that contain X

5. 
Example
4
.
0
5
2
|
T
|
)
Beer
Diaper,
,
Milk
(




s
67
.
0
3
2
)
Diaper
,
Milk
(
)
Beer
Diaper,
Milk,
(





c
If we had the following rule
-:
{
Milk, Diaper
}
 {Beer}
Find both Support (s) and Confidence (c)
TID Items
1 Bread, Milk
2 Bread, Diaper, Beer, Eggs
3 Milk, Diaper, Beer, Coke
4 Bread, Milk, Diaper, Beer
5 Bread, Milk, Diaper, Coke

6. FREQUENT ITEMSET
 Frequent Itemset
An itemset whose support is greater than or equal to a minsup
threshold
.
Given a set of transactions T, the goal of association rule mining is to find
all rules having
-
support ≥ minsup threshold
-
confidence ≥ minconf threshold

7. 
There are many algorithms to generate Frequent Itemset We
will study Apriori which has been improved by using FP tree
algorithm
.
Aproiri algorithm
:
The Apriori principle is an effective way to eliminate
some of the
candidate itemsets
.
Frequent Itemset Generation

8. Computational Complexity
Given d unique items
:
Total number of itemsets = 2d
Total number of possible association rules
:
1
2
3 1


 
d
d
If d=6, R = 602 rules

9. Frequent Itemset Generation Strategies
Reduce the number of candidates (M) The Apriori principle is an
effective way to eliminate some of the candidate itemsets without counting
their support values
.
-
Complete search: M=2d
-
Use pruning techniques to reduce M
- .
If an itemset is frequent, then all of its subsets must also be frequent

10. Illustrating Apriori Principle

12. THE APRIORI ALGORITHM FOR FINDING
LARGE ITEMSETS EFFICIENTLY IN BIG DBS
1
:
Find all large 1-itemsets
2
:
For (k = 2 ; while Lk-1 is non-empty; k++)
3
{ :
Ck = apriori-gen(Lk-1)
4
:
For each c in Ck, initialise c.count to zero
5
:
For all records r in the DB
6
{ :
Cr = subset(Ck, r); For each c in Cr , c.count
} ++
7
:
Set Lk := all c in Ck whose count >= minsup
8
*/ } :
end -- return all of the Lk sets
.

13. DISCUSSION OF THE APRIORI ALGORITHM
• The running time is in the worst case O(2d
)
– Pruning really prunes in practice
• It makes multiple passes over the dataset
– One pass for every level k
• Multiple passes over the dataset is inefficient when we have thousands
of candidates and millions of transactions

14. FP-TREE
• A FP-Tree: is a tree data structure that represents the
database in a compact way. It is constructed by mapping each
frequency ordered transaction onto a path in the FP-Tree.

15. OVERVIEW OF FP-GROWTH: IDEAS
 Compress a large database into a compact, Frequent-Pattern tree (FP-tree)
structure
 highly compacted, but complete for frequent pattern mining
 avoid costly repeated database scans
 Develop an efficient, FP-tree-based frequent pattern mining method (FP-
growth)
 A divide-and-conquer methodology: decompose mining tasks into smaller
ones
 Avoid candidate generation: sub-database test only

16. CONSTRUCT FP-TREE
Two Steps:
1- Scan the transaction DB for the first time, find frequent items (single
item patterns) and order them into a list L in frequency descending
order.
e.g., L={f:4, c:4, a:3, b:3, m:3, p:3}
In the format of (item-name, support)
2- For each transaction, order its frequent items according to the order in
L; Scan DB the second time, construct FP-tree by putting each
frequency ordered transaction onto it

17. FP-TREE EXAMPLE
:
 Step 1: Scan DB for the first time to generate L
 Let min_support=3
TID list of items
100 {f, a, c, d, g, i, m, p}
200 {a, b, c, f, l, m, o}
300 {b, f, h, j, o}
400 {b, c, k, s, p}
500 {a, f, c, e, l, p, m, n}
Item frequency
f 4
c 4
a 3
b 3
m 3
p 3
By-Product of First
Scan of Database

18.  Step 2: scan the DB for the second time, order frequent items
in each transaction
TID list of items (ordered) frequent items
100 {f, a, c, d, g, i, m, p} {f, c, a, m, p}
200 {a, b, c, f, l, m, o} {f, c, a, b, m}
300 {b, f, h, j, o} {f, b}
400 {b, c, k, s, p} {c, b, p}
500 {a, f, c, e, l, p, m, n} {f, c, a, m, p}

19.  Step 2: construct FP-tree
}{ {
f, c, a, m, p
}
}{
f:1
c:1
a:1
m:1
p:1
NOTE: Each transaction
corresponds to one path
in the FP-tree
}{
{
f, c, a, b, m
}
f:2
c:2
a:2
b:1
m:1
m:1
p:1

20.  Step 2: construct FP-tree
}{
f:3
c:2
a:2
b:1
p:1 m:1
b:1
m:1
{
f, b
}
}{
f:4 c:1
b:1
p:1
b:1
c:3
a:3
b:1
m:2
p:2 m:1
{
c, b, p
}
c:1
b:1
p:1
}{
f:3
c:2
a:2
b:1
m:1
p:1 m:1
b:1
{
f, c, a, m, p
}
Node-Link

21. Final FP-tree
}{
f:4 c:1
b:1
p:1
b:1
c:3
a:3
b:1
m:2
p:2 m:1
Header Table
Item head
f
c
a
b
m
p

22. ADVANTAGES OF THE FP-TREE STRUCTURE
 The most significant advantage of the FP-tree
 Scan the DB only twice .
 Completeness:
 the FP-tree contains all the information related to mining frequent patterns (given the min-support
threshold).
 Compactness:
 FP-tree does not generate an exponential number of nodes.
 The items ordered in the support-descending order indicate that FP-tree structure is
usually highly compact.
 The size of the tree is bounded by the occurrences of frequent items
 The height of the tree is bounded by the maximum number of items in a transaction

23. *** the time complexity should be O(n2
) if the number of
unique items in the dataset is n. The complexity depends on
searching of paths in FP tree for each element of the header
table, which depends on the depth of the tree. Maximum depth
of the tree is upper-bounded by n for each of the conditional
trees. Thus the order is: O (No. of items in header table *
maximum depth of tree)= O(n*n).

24. Thank you