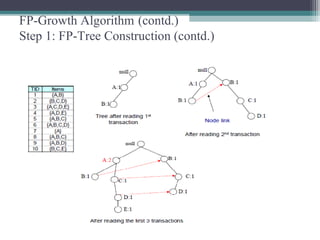
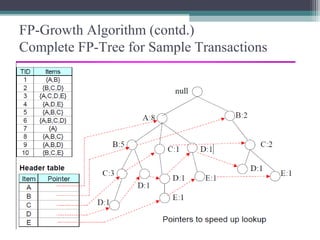
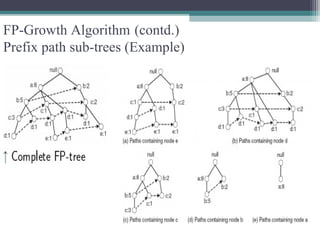
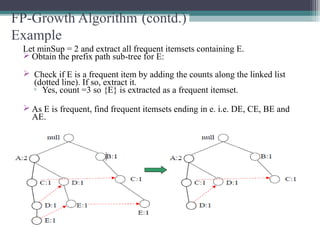
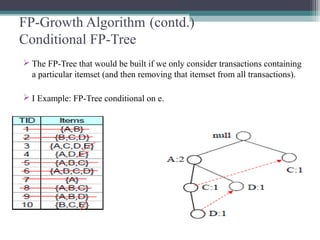
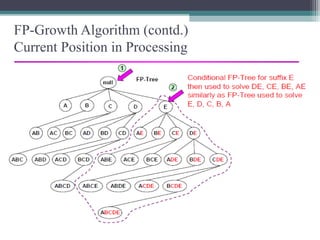
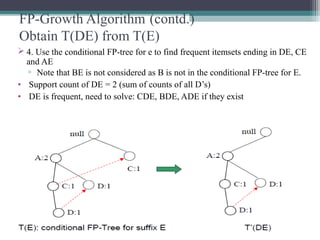
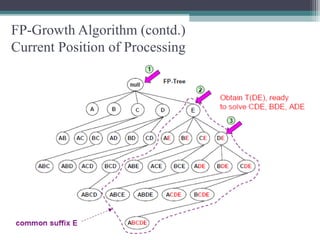
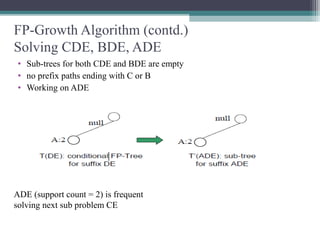
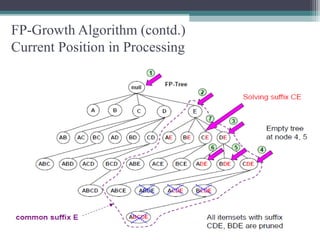
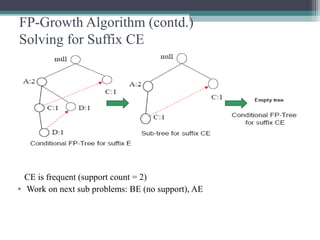
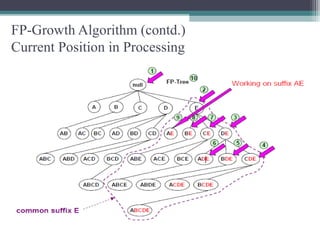
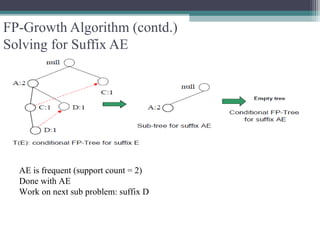
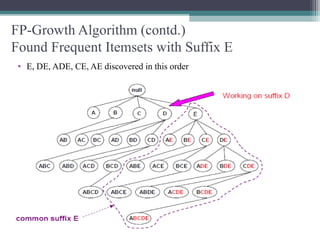
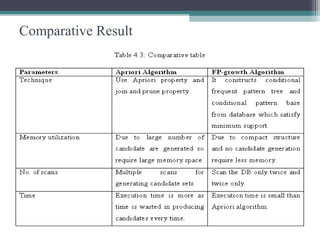
This document summarizes a seminar presentation comparing the Apriori and FP-Growth algorithms for association rule mining. The document introduces association rule mining and frequent itemset mining. It then describes the Apriori algorithm, including its generate-and-test approach and bottlenecks. Next, it explains the FP-Growth algorithm, including how it builds an FP-tree to efficiently extract frequent itemsets without candidate generation. Finally, it provides results comparing the performance of the two algorithms and concludes that FP-Growth is more efficient for mining long patterns.

1. A SEMINAR ON
THE COMPARATIVE STUDY OF
APRIORI AND
FP-GROWTH ALGORITHM FOR
ASSOCIATION RULE MINING
Under the Guidance of: By:
Mrs. Sankirti Shiravale
Deepti Pawar

2. Contents
Introduction
Literature Survey
Apriori Algorithm
FP-Growth Algorithm
Comparative Result
Conclusion
Reference

3. Introduction
Data Mining: It is the process of discovering interesting patterns (or
knowledge) from large amount of data.
• Which items are frequently purchased with milk?
• Fraud detection: Which types of transactions are likely to be fraudulent,
given the demographics and transactional history of a particular customer?
• Customer relationship management: Which of my customers are likely to
be the most loyal, and which are most likely to leave for a competitor?
Data Mining helps extract such information

4. Introduction (contd.)
Why Data Mining?
Broadly, the data mining could be useful to answer the queries on :
• Forecasting
• Classification
• Association
• Clustering
• Making the sequence

5. Introduction (contd.)
Data Mining Applications
• Aid to marketing or retailing
• Market basket analysis (MBA)
• Medicare and health care
• Criminal investigation and homeland security
• Intrusion detection
• Phenomena of “beer and baby diapers”
And many more…

6. Literature Survey
Association Rule Mining
• Proposed by R. Agrawal in 1993.
• It is an important data mining model studied extensively by the database and
data mining community.
• Initially used for Market Basket Analysis to find how items purchased by
customers are related.
• Given a set of transactions, find rules that will predict the occurrence of an
item based on the occurrences of other items in the transaction

7. Literature Survey (contd.)
Frequent Itemset
• Itemset TID Items
▫ A collection of one or more items
1 Bread, Milk
 Example: {Milk, Bread, Diaper}
2 Bread, Diaper, Beer, Eggs
▫ k-itemset
3 Milk, Diaper, Beer, Coke
 An itemset that contains k items
4 Bread, Milk, Diaper, Beer
• Support count (σ)
5 Bread, Milk, Diaper, Coke
▫ Frequency of occurrence of an itemset
▫ E.g. σ({Milk, Bread, Diaper}) = 2
• Support
▫ Fraction of transactions that contain an itemset
▫ E.g. s( {Milk, Bread, Diaper} ) = 2/5
• Frequent Itemset
▫ An itemset whose support is greater than or equal
to a minsup threshold

8. Literature Survey (contd.)
Association Rule
• Association Rule
▫ An implication expression of TID Items
the form X → Y, where X and 1 Bread, Milk
Y are itemsets. 2 Bread, Diaper, Beer, Eggs
▫ Example:
3 Milk, Diaper, Beer, Coke
{Milk, Diaper} → {Beer}
4 Bread, Milk, Diaper, Beer
• Rule Evaluation Metrics 5 Bread, Milk, Diaper, Coke
▫ Support (s)
 Fraction of transactions that Example:
contain both X and Y {Milk, Diaper} ⇒ Beer
▫ Confidence (c)
 Measures how often items in σ (Milk , Diaper, Beer) 2
Y appear in transactions that s= = = 0.4
contain X. |T| 5
σ (Milk, Diaper, Beer) 2
c= = = 0.67
σ (Milk, Diaper ) 3

9. Apriori Algorithm
• Apriori principle:
▫ If an itemset is frequent, then all of its subsets must also be frequent
• Apriori principle holds due to the following property of the support
measure:
▫ Support of an itemset never exceeds the support of its subsets
▫ This is known as the anti-monotone property of support

10. Apriori Algorithm (contd.)
The basic steps to mine the frequent elements are as follows:
• Generate and test: In this first find the 1-itemset frequent elements L1 by
scanning the database and removing all those elements from C which
cannot satisfy the minimum support criteria.
• Join step: To attain the next level elements Ck join the previous frequent
elements by self join i.e. Lk-1*Lk-1 known as Cartesian product of Lk-1 .
i.e. This step generates new candidate k-itemsets based on joining Lk-1
with itself which is found in the previous iteration. Let Ck denote
candidate k-itemset and Lk be the frequent k-itemset.
• Prune step: This step eliminates some of the candidate k-itemsets using the
Apriori property. A scan of the database to determine the count of each
candidate in Ck would result in the determination of Lk (i.e., all candidates
having a count no less than the minimum support count are frequent by
definition, and therefore belong to Lk). Step 2 and 3 is repeated until no
new candidate set is generated.

11. Database C^1 L1
TID Set-of- itemsets
TID Items Itemset Support
100 { {1},{3},{4} }
100 134 {1} 2
200 { {2},{3},{5} }
200 235 {2} 3
300 { {1},{2},{3},{5} }
300 1235 {3} 3
400 { {2},{5} }
400 25 {5} 3
C2
C^2 L2
itemset TID Set-of- itemsets Itemset Support
{1 2} 100 { {1 3} } {1 3} 2
{1 3} 200 { {2 3},{2 5} {3 5} } {2 3} 3
{1 5} 300 { {1 2},{1 3},{1 5}, {2 5} 3
{2 3} {2 3}, {2 5}, {3 5} } {3 5} 2
{2 5} 400 { {2 5} }
{3 5}
C^3 L3
C3
TID Set-of- itemsets
Itemset Support
itemset 200 { {2 3 5} }
{2 3 5} 2
{2 3 5} 300 { {2 3 5} }

12. Apriori Algorithm (contd.)
Bottlenecks of Apriori
• It is no doubt that Apriori algorithm successfully finds the frequent
elements from the database. But as the dimensionality of the database
increase with the number of items then:
• More search space is needed and I/O cost will increase.
• Number of database scan is increased thus candidate generation will
increase results in increase in computational cost.

13. FP-Growth Algorithm
 FP-Growth: allows frequent itemset discovery without candidate itemset
generation. Two step approach:
▫ Step 1: Build a compact data structure called the FP-tree
 Built using 2 passes over the data-set.
▫ Step 2: Extracts frequent itemsets directly from the FP-tree

14. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction
 FP-Tree is constructed using 2 passes
over the data-set:
Pass 1:
▫ Scan data and find support for each
item.
▫ Discard infrequent items.
▫ Sort frequent items in decreasing
order based on their support.
• Minimum support count = 2
• Scan database to find frequent 1-itemsets
• s(A) = 8, s(B) = 7, s(C) = 5, s(D) = 5, s(E) = 3
• 􀁺 Item order (decreasing support): A, B, C, D, E
Use this order when building the FP-
Tree, so common prefixes can be shared.

15. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction
Pass 2:
Nodes correspond to items and have a counter
1. FP-Growth reads 1 transaction at a time and maps it to a path
2. Fixed order is used, so paths can overlap when transactions share items
(when they have the same prefix ).
▫ In this case, counters are incremented
3. Pointers are maintained between nodes containing the same item,
creating singly linked lists (dotted lines)
▫ The more paths that overlap, the higher the compression. FP-tree
may fit in memory.
4. Frequent itemsets extracted from the FP-Tree.

16. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction (contd.)

17. FP-Growth Algorithm (contd.)
Complete FP-Tree for Sample Transactions

18. FP-Growth Algorithm (contd.)
Step 2: Frequent Itemset Generation
 FP-Growth extracts frequent itemsets from the FP-tree.
 Bottom-up algorithm - from the leaves towards the root
 Divide and conquer: first look for frequent itemsets ending in e, then de,
etc. . . then d, then cd, etc. . .
 First, extract prefix path sub-trees ending in an item(set). (using the linked
lists)

19. FP-Growth Algorithm (contd.)
Prefix path sub-trees (Example)

20. FP-Growth Algorithm (contd.)
Example
Let minSup = 2 and extract all frequent itemsets containing E.
 Obtain the prefix path sub-tree for E:
 Check if E is a frequent item by adding the counts along the linked list
(dotted line). If so, extract it.
▫ Yes, count =3 so {E} is extracted as a frequent itemset.
 As E is frequent, find frequent itemsets ending in e. i.e. DE, CE, BE and
AE.
 E nodes can now be removed

21. FP-Growth Algorithm (contd.)
Conditional FP-Tree
 The FP-Tree that would be built if we only consider transactions containing
a particular itemset (and then removing that itemset from all transactions).
 I Example: FP-Tree conditional on e.

22. FP-Growth Algorithm (contd.)
Current Position in Processing

23. FP-Growth Algorithm (contd.)
Obtain T(DE) from T(E)
 4. Use the conditional FP-tree for e to find frequent itemsets ending in DE, CE
and AE
▫ Note that BE is not considered as B is not in the conditional FP-tree for E.
• Support count of DE = 2 (sum of counts of all D’s)
• DE is frequent, need to solve: CDE, BDE, ADE if they exist

24. FP-Growth Algorithm (contd.)
Current Position of Processing

25. FP-Growth Algorithm (contd.)
Solving CDE, BDE, ADE
• Sub-trees for both CDE and BDE are empty
• no prefix paths ending with C or B
• Working on ADE
ADE (support count = 2) is frequent
solving next sub problem CE

26. FP-Growth Algorithm (contd.)
Current Position in Processing

27. FP-Growth Algorithm (contd.)
Solving for Suffix CE
CE is frequent (support count = 2)
• Work on next sub problems: BE (no support), AE

28. FP-Growth Algorithm (contd.)
Current Position in Processing

29. FP-Growth Algorithm (contd.)
Solving for Suffix AE
AE is frequent (support count = 2)
Done with AE
Work on next sub problem: suffix D

30. FP-Growth Algorithm (contd.)
Found Frequent Itemsets with Suffix E
• E, DE, ADE, CE, AE discovered in this order

31. FP-Growth Algorithm (contd.)
Example (contd.)
Frequent itemsets found (ordered by suffix and order in which the are
found):

32. Comparative Result

33. Conclusion
It is found that:
• FP-tree: a novel data structure storing compressed, crucial information
about frequent patterns, compact yet complete for frequent pattern mining.
• FP-growth: an efficient mining method of frequent patterns in large
Database: using a highly compact FP-tree, divide-and-conquer method in
nature.
• Both Apriori and FP-Growth are aiming to find out complete set of patterns
but, FP-Growth is more efficient than Apriori in respect to long patterns.

34. References
1. Liwu, ZOU, Guangwei, REN, “The data mining algorithm analysis for
personalized service,” Fourth International Conference on Multimedia
Information Networking and Security, 2012.
2. Jun TAN, Yingyong BU and Bo YANG, “An Efficient Frequent Pattern
Mining Algorithm”, Sixth International Conference on Fuzzy Systems and
Knowledge Discovery, 2009.
3. Wei Zhang, Hongzhi Liao, Na Zhao, “Research on the FP Growth Algorithm
about Association Rule Mining”, International Seminar on Business and
Information Management, 2008.
4. S.P Latha, DR. N.Ramaraj. “Algorithm for Efficient Data Mining”. In Proc.
Int’ Conf. on IEEE International Computational Intelligence and Multimedia
Applications, 2007.

35. References (contd.)
5. Dongme Sun, Shaohua Teng, Wei Zhang, Haibin Zhu. “An Algorithm to
Improve the Effectiveness of Apriori”. In Proc. Int’l Conf. on 6th IEEE
International Conf. on Cognitive Informatics (ICCI'07), 2007.
6. Daniel Hunyadi, “Performance comparison of Apriori and FP-Growth
algorithms in generating association rules”, Proceedings of the European
Computing Conference, 2006.
7. By Jiawei Han, Micheline Kamber, “Data mining Concepts and
Techniques” Morgan Kaufmann Publishers, 2006.
8. Tan P.-N., Steinbach M., and Kumar V. “Introduction to data mining”
Addison Wesley Publishers, 2006.

36. References (contd.)
9. Han.J, Pei.J, and Yin. Y. “Mining frequent patterns without candidate
generation”. In Proc. ACM-SIGMOD International Conf. Management
of Data (SIGMOD), 2000.
10. R. Agrawal, Imielinski.t, Swami.A. “Mining Association Rules between
Sets of Items in Large Databases”. In Proc. International Conf. of the
ACM SIGMOD Conference Washington DC, USA, 1993.