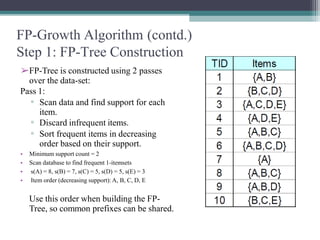
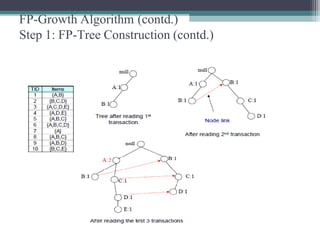
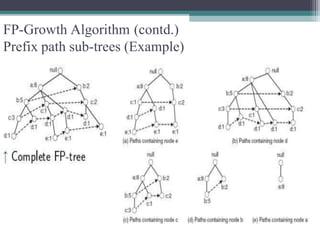
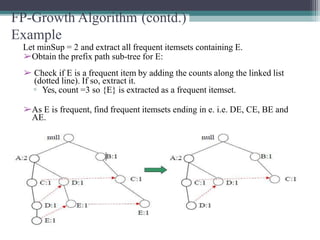
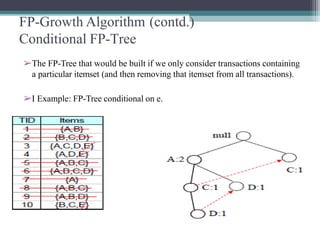
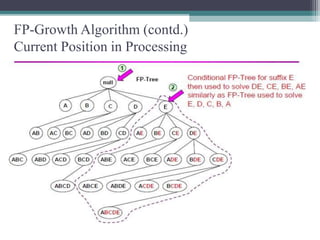
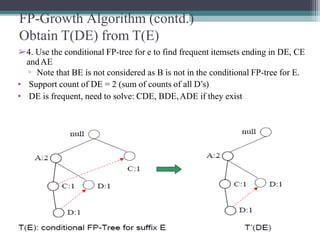
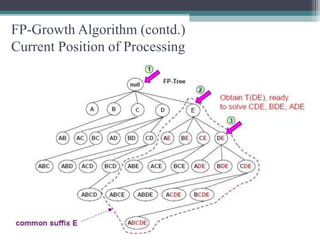
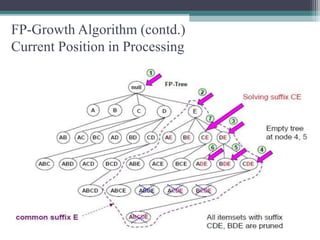
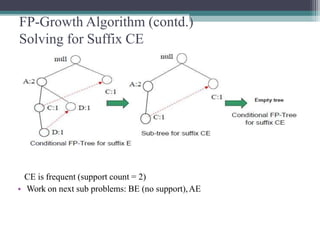
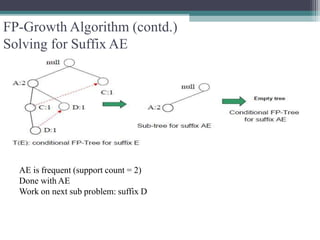
The FP-Growth algorithm allows for the efficient discovery of frequent itemsets without candidate generation. It uses a two-step approach: 1) building a compact FP-tree from transaction data, and 2) extracting frequent itemsets directly from the FP-tree. It proceeds by finding prefix path sub-trees in the FP-tree and recursively mining conditional frequent patterns.

1. FP-Growth Algorithm
➢FP-Growth: allows frequent itemset discovery without candidate itemset
generation. Two step approach:
▫ Step 1: Build a compact data structure called the FP-tree
Built using 2 passes over the data-set.
▫ Step 2: Extracts frequent itemsets directly from the FP-tree

2. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction
➢FP-Tree is constructed using 2 passes
over the data-set:
Pass 1:
▫ Scan data and find support for each
item.
▫ Discard infrequent items.
▫ Sort frequent items in decreasing
order based on their support.
• Minimum support count = 2
• Scan database to find frequent 1-itemsets
• s(A) = 8, s(B) = 7, s(C) = 5, s(D) = 5, s(E) = 3
• Item order (decreasing support): A, B, C, D, E
Use this order when building the FP-
Tree, so common prefixes can be shared.

3. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction
Pass 2:
Nodes correspond to items and have a counter
1. FP-Growth reads 1 transaction at a time and maps it to a path
▫
2. Fixed order is used, so paths can overlap when transactions share items
(when they have the same prefix ).
In this case, counters are incremented
▫
3. Pointers are maintained between nodes containing the same item,
creating singly linked lists (dotted lines)
The more paths that overlap, the higher the compression. FP-tree
may fit in memory.
4. Frequent itemsets extracted from the FP-Tree.

4. FP-Growth Algorithm (contd.)
Step 1: FP-Tree Construction (contd.)

5. FP-Growth Algorithm (contd.)
Complete FP-Tree for Sample Transactions

6. FP-Growth Algorithm (contd.)
Step 2: Frequent Itemset Generation
➢FP-Growth extracts frequent itemsets from the FP-tree.
➢Bottom-up algorithm - from the leaves towards the root
➢Divide and conquer: first look for frequent itemsets ending in e, then de,
etc. . . then d, then cd, etc. . .
➢First, extract prefix path sub-trees ending in an item(set). (using the linked
lists)

7. FP-Growth Algorithm (contd.)
Prefix path sub-trees (Example)

8. FP-Growth Algorithm (contd.)
Example
Let minSup = 2 and extract all frequent itemsets containing E.
➢Obtain the prefix path sub-tree for E:
➢ Check if E is a frequent item by adding the counts along the linked list
(dotted line). If so, extract it.
▫ Yes, count =3 so {E} is extracted as a frequent itemset.
➢As E is frequent, find frequent itemsets ending in e. i.e. DE, CE, BE and
AE.
➢E nodes can now be removed

9. FP-Growth Algorithm (contd.)
Conditional FP-Tree
➢The FP-Tree that would be built if we only consider transactions containing
a particular itemset (and then removing that itemset from all transactions).
➢I Example: FP-Tree conditional on e.

10. FP-Growth Algorithm (contd.)
Current Position in Processing

11. FP-Growth Algorithm (contd.)
Obtain T(DE) from T(E)
➢4. Use the conditional FP-tree for e to find frequent itemsets ending in DE, CE
andAE
▫ Note that BE is not considered as B is not in the conditional FP-tree for E.
•
•
Support count of DE = 2 (sum of counts of all D’s)
DE is frequent, need to solve: CDE, BDE,ADE if they exist

12. FP-Growth Algorithm (contd.)
Current Position of Processing

13. FP-Growth Algorithm (contd.)
Solving CDE, BDE, ADE
• Sub-trees for both CDE and BDE are empty
• no prefix paths ending with C or B
• Working onADE
ADE (support count = 2) is frequent
solving next sub problem CE

14. FP-Growth Algorithm (contd.)
Current Position in Processing

15. FP-Growth Algorithm (contd.)
Solving for Suffix CE
CE is frequent (support count = 2)
• Work on next sub problems: BE (no support),AE

16. FP-Growth Algorithm (contd.)
Current Position in Processing

17. FP-Growth Algorithm (contd.)
Solving for Suffix AE
AE is frequent (support count = 2)
Done with AE
Work on next sub problem: suffix D

18. FP-Growth Algorithm (contd.)
Found Frequent Itemsets with Suffix E
• E, DE,ADE, CE,AE discovered in this order

19. FP-GrowthAlgorithm (contd.)
Example (contd.)
Frequent itemsets found (ordered by suffix and order in which the are
found):

20. Comparative Result

21. Conclusion
It is found that:
• FP-tree: a novel data structure storing compressed, crucial information
about frequent patterns, compact yet complete for frequent pattern mining.
• FP-growth: an efficient mining method of frequent patterns in large
Database: using a highly compact FP-tree, divide-and-conquer method in
nature.
• Both Apriori and FP-Growth are aiming to find out complete set of patterns
but, FP-Growth is more efficient thanApriori in respect to long patterns.

22. References
1. Liwu, ZOU, Guangwei, REN, “The data mining algorithm analysis for
personalized service,” Fourth International Conference on Multimedia
Information Networking and Security, 2012.
2. Jun TAN,Yingyong BU and Bo YANG, “An Efficient Frequent Pattern
Mining Algorithm”, Sixth International Conference on Fuzzy Systems and
Knowledge Discovery, 2009.
3. Wei Zhang, Hongzhi Liao, Na Zhao, “Research on the FP Growth Algorithm
about Association Rule Mining”, International Seminar on Business and
Information Management, 2008.
4. S.P Latha, DR. N.Ramaraj. “Algorithm for Efficient Data Mining”. In Proc.
Int’Conf. on IEEE International Computational Intelligence and Multimedia
Applications, 2007.

23. References (contd.)
5. Dongme Sun, Shaohua Teng, Wei Zhang, Haibin Zhu. “An Algorithm to
Improve the Effectiveness of Apriori”. In Proc. Int’l Conf. on 6th IEEE
International Conf. on Cognitive Informatics (ICCI'07), 2007.
6. Daniel Hunyadi, “Performance comparison of Apriori and FP-Growth
algorithms in generating association rules”, Proceedings of the European
Computing Conference, 2006.
7. By Jiawei Han, Micheline Kamber, “Data mining Concepts and
Techniques” Morgan Kaufmann Publishers, 2006.
8. Tan P.-N., Steinbach M., and Kumar V.“Introduction to data mining”
Addison Wesley Publishers, 2006.

24. References (contd.)
9. Han.J, Pei.J, and Yin. Y.“Mining frequent patterns without candidate
generation”. In Proc. ACM-SIGMOD International Conf. Management
of Data (SIGMOD), 2000.
10. R. Agrawal, Imielinski.t, Swami.A. “Mining Association Rules between
Sets of Items in Large Databases”. In Proc. International Conf. of the
ACM SIGMOD Conference Washington DC, USA, 1993.