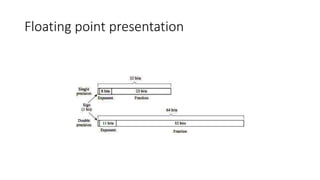
This document discusses floating point number representation in IEEE-754 format. It explains that floating point numbers consist of a sign bit, exponent, and mantissa. It describes single and double precision formats, which use excess-127 and excess-1023 exponent biases respectively. Examples are given of representing sample numbers in both implicit and explicit normalized forms using single and double precision formats.

1. IEEE-754 Floating point
representation(Unit-2)
Prepared by : Snehalata Agasti
CSE department

2. Floating point representation
• Two types of Number system presentation
➢Fixed point representation
➢Floating point representation
Floating point representation of number consists of 3 parts
➢ Sign bit
➢Exponent
➢Mantissa
• Normally represented as
• Two formats used for representation
➢Single precision format/Excess-127 format
➢Double precision format/Excess-1023 format
S E M

3. Floating Point
• Floating point consists of two parts:- Mantissa
Exponent
• Let number is 14.5 .
• Point before number is Exponent.
• Number after point is Mantissa.
• Used to represent very small numbers like fractions and very large
numbers.
• Floating point representation is used in High level languages in the form of
float(32-bits) and double(64-bits).

4. Floating point presentation

5. Presentation of Floating point Number
• We may present the floating point number using Single precision
format/double precision format.
• We know that floating point is represented as :-
• Number:
• Single precision format is also known as Excess-127 format.
S E M
Exponent
1011 .1
Mantissa

6. Explanation of Exponent
• Exponent is of two types :- original exponent [e]
• - Stored Exponent [E’]
• E’ is computed using formula:-
• Bias is same as Excess-X code. E.g. Excess-3 code means 0 will be counted
as 0+3=3, 1 as 1+3=4.
• Similarly if original bias is e and biased exponent is in the form Excess-32
then Biased Exponent is e+32.
• If exponent is presented in k-bits then bias value is 2k-1 -1.
• Note -: Biased Exponent means Exponent is not stored directly. It is stored
as original bias + Excess-x format.[x value is anything.]
E’ =e+ bias

7. Mantissa
• Mantissa is number after the point.
• When we are going to present mantissa in memory it is presented in
normalised format.
• In Explicit normalised form number is present after the point. E.g.
1011.1 -> number can be normalise as 0.10111 x 2 4 . [instead of 10 base 2 is used]
Implicit
Normalized
form
Explicit
Normalised
Form

8. Cont…
• In Explicit normalised form point is present by leaving one bit value
and that value is 1. Means presented as 1.---
• Let the number is 1011.1 .
• Implicit Presentation of number in memory 1.0111 x 2 3.
• Original exponent(e) is 3.
• Biased exponent is(E’)= 127+3=130 [As we are presenting using
excess-127 format]

9. Explanation of problem using Explicit
normalised form
• 11.5 is represented as 1011.1 in binary system.
• Normalised value of 1011.1 is 0.10111 x 24 in explicit normalised
form.
• Now mantissa is 0.10111 and represented in 23 bit.
• Exponent is presented in 8 bit. Biased exponent(E’) is 127+4=131.
Binary of 131 is 10000011.
• Sign bit will be 0 as number is positive. Only 1 bit is left for sign.
0 1 0 0 0 0 0 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Exponent
Sign Mantissa

10. Floating point representation using implicit
normalised form
• Floating point number=13.5 .
• Binary presentation of number (13.5)10 = (1101.1)2 .
• Now implicit normalised form of the number is 1101.1 = 1.1011 x23 .
• So original bias[e] = 3 .
• Stored bias[E’] = 127+3 = 130 = 10000010
• Mantissa is .1011
• Now floating point presentation of number is
0 10000010 1011000……………0
Sign bit Exponent Mantissa

11. Implicit and Explicit presentation of Floating
point number in double precision format
• (13.5)10 = (1101.1)2
0 000 1000 0011 11011 000000 …. …0
0 000 1000 0010 1011 000 ……….. …0
Sign bit(1) Exponent(11) Mantissa(53)
Explicit Representation of Floating point Number
Implicit representation of floating point number