The document summarizes computer arithmetic and the arithmetic logic unit (ALU). It discusses:
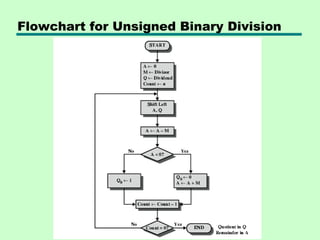
1) The ALU handles integer and floating point calculations. It may have a separate floating point unit.
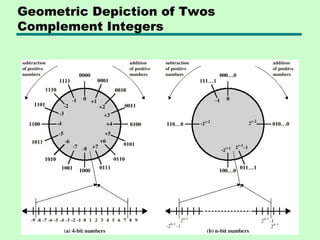
2) There are different methods for representing integers like sign-magnitude and two's complement. Two's complement is commonly used.
3) Floating point numbers use a sign, significand, and exponent to represent real numbers in a normalized format like ±.significand × 2exponent.