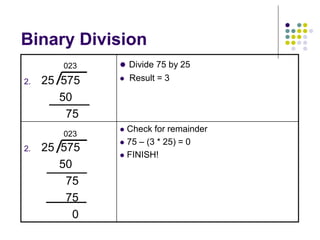
The document provides an in-depth overview of binary arithmetic, detailing operations such as addition, subtraction, multiplication, and division, all performed using binary representations. It explains methods such as two’s complement for subtraction and the shift-and-add technique for multiplication and division. Additionally, it touches on octal and hexadecimal arithmetic, showing how these systems convert to binary for operations.

1. Binary Arithmetic

2. BinaryArithmetic
• Binary arithmetic is essential part of all the digital
computers and many other digital system.
• Binary arithmetic is used in digital systems mainly
because the numbers (decimal and floating-point
numbers) are stored in binary format in most
computer systems.
• All arithmetic operations such as addition,
subtraction, multiplication, and division are done
in binary representation of numbers.

3. Binary Addition
 The steps used for a computer to complete
addition are usually greater than a human, but
their processing speed is far superior.
RULES
 0 + 0 = 0
 0 + 1 = 1
 1 + 0 = 1
 1 + 1 = 0 (With 1 to carry)
 1 + 1 + 1 = 1 (With 1 to carry)

4. Binary Addition
EXAMPLE
1 0 0 1
1 0 1 1
+

5. Binary Addition
EXAMPLE
1 0 01 1
1 0 1 1
0
+

6. Binary Addition
EXAMPLE
1 01 01 1
1 0 1 1
0 0
+

7. Binary Addition
EXAMPLE
1 01 01 1
1 0 1 1
1 0 0
+

8. Binary Addition
EXAMPLE
11 01 01 1
1 0 1 1
0 1 0 0
+

9. Binary Addition
EXAMPLE
11 01 01 1
1 0 1 1
1 0 1 0 0
+

10. Binary Addition
CHECK THE ANSWER
9
11
20
+

11. Activity 1
Perform the following additions in binary.
 10110 + 4010 =
 32010 + 1810 =
 7610 + 27110 =

12. Binary Subtraction

13. Binary Subtraction
 Computers have trouble performing
subtractions so the following rule should be
employed:
“X – X is the same as
X + -X”
 This is where two’s complement is used.

14. Binary Subtraction
RULES
2. Convert the number to binary.
3. Perform two’s complement on the second
number.
4. Add both numbers together.

15. Binary Subtraction
EXAMPLE 1
Convert 12 - 8 using two’s complement.
3. Convert to binary
12 = 000011002

8 = 000010002
Perform one’s complement on the 810
000010002
111101112

16. Binary Subtraction
EXAMPLE 1
2. Perform two’s complement.
1 1 1 1 0 1 1 12
0 0 0 0 0 0 0 12
1 1 1 1 1 0 0 02
6. Add the two numbers together.
= 1 0 0 0 0 0 1 0 02 (Ignore insignificant bits)
+

17. Binary Subtraction
EXAMPLE 2
What happens if the first number is larger than
the second?
Try 610 - 1010

18. Binary Subtraction
EXAMPLE 2
2. Convert to binary
6 = 000001102

10 = 000010102
Perform one’s complement on the 1010
000010102
111101012

19. Binary Subtraction
EXAMPLE 2
2. Perform two’s complement.
1 1 1 1 0 1 0 12
2
= 1 1 1 1 0 1 1 02
0 0 0 0 0 0 0 1+

20. Binary Subtraction
EXAMPLE 2
2. Add the two numbers together.
0 0 0 0 0 1 1 02
1 1 1 1 0 1 1 02
1
= 1 1 1 1 1 0 02 (Ends with a negative bit)
+

21. Binary Subtraction
EXAMPLE 2
2. Perform one’s complement on the result
1 1 1 1 1 1 0 02
0 0 0 0 0 0 1 12
5. Add 1 to the result.
0 0 0 0 0 0 1 12
0 0 0 0 0 0 0 12
= 0 0 0 0 0 1 0 02
+

22. Binary Subtraction
EXAMPLE 2
2. We then add the sign bit back.
0 0 0 0 0 1 0 02
= 1 0 0 0 0 1 0 02

23. Activity
2
Perform the following subtractions.
3. 22 - 8 =
4. 76 - 11 =
5. 6 - 44 =

24. Binary Multiplication
 Multiplication follows the general principal of
shift and add.
 The rules include:




0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1

25. Binary Multiplication
EXAMPLE 1
Complete 15 * 5 in binary.
3. Convert to binary
15 = 000011112
5 = 000001012
6. Ignore any insignificant zeros.
000011112
000001012
x

26. Binary Multiplication
EXAMPLE 1
2. Multiply the first number.
1 1 1 12
1 0 1 2
1 1 1 1
7. Now this is where the shift and takes place.
x
1111 x 1 = 1111

27. Binary Multiplication
EXAMPLE 1
2. Shift one place to the left and multiple the
second digit.
1 1 1 12
1 0 1 2
1 1 1 1
0 0 0 0 0
x
1111 x 0 = 0000
Shift One Place

28. Binary Multiplication
EXAMPLE 1
2. Shift one place to the left and multiple the
third digit.
1 1 1 12
1 0 1 2
1 1 1 1
0 0 0 0 0
1 1 1 1 0 0
x
1111 x 1 = 1111
Shift One Place

29. Binary Multiplication
EXAMPLE 1
2. Add the total of all the steps.
1 1 1 1
0 0 0 0 0
1 1 1 1 0 0
1 0 0 1 0 1 1
8. Convert back to decimal to check.
+

30. Activity
3
Calculate the following using binary
multiplication shift and add.




12 * 3 = 1 0 0 1 0 02
13 * 5 = 1 0 0 0 0 0 12
97 * 20 = 1 1 1 1 0 0 1 0 1 0 02
121 * 67 = 1 1 1 1 1 1 0 1 0 1 0 1 12

31. Binary Division
 Division in binary is similar to long division in
decimal.
 It uses what is called a shift and subtract
method.

32. Binary Division
EXAMPLE 1
Complete 575 / 25 using long division.
2.
0
25 575
Take the first digit of 575 (5) and see if 25
will go into it.
If it can not put a zero above and take the
next number.
02  How many times does 25 go into 57?
2. 25 575
TWICE

33. Binary Division
02  How much is left over?
2. 25 575  57 – (25 * 2) = 7
50
7
02
 Drop down the next value
2. 25 575
50
75

34. Binary Division
023  Divide 75 by 25
2. 25 575  Result = 3
50
75
023
 Check for remainder
 75 – (3 * 25) = 0
 FINISH!
2. 25 575
50
75
75
0

35. Binary Division
 Complete the following:
 25/5
Step 1: Convert both numbers to binary.
25 = 1 1 0 0 1
5 = 1 0 1
Step 2: Place the numbers accordingly:
1 0 1 1 1 0 0 1

36. Binary Division
Step 3: Determine if 1 0 1 (5) will fit into the
first bit of dividend.
1 0 1 1
1 0 1(5) will not fit into 1(1)
Step 4: Place a zero above the first bit and try
the next bit.
1 1 0 0

37. Binary Division
1 1 0 0
Step 5: Determine if 1 0 1 (5) will fit into the
next two bits of dividend.
0
1 0 1 1
1 0 1(5) will not fit into 1 1(3)
Step 6: Place a zero above the second bit and
try the next bit.

38. Binary Division
• Step 7: Determine if 1 0 1 (5) will fit into the
next three bits of dividend.
• 0 0
• 1 0 1 1
• 1 0 1(5) will fit into 1 1 0(6)
• Step 8: Place a one above the third bit and
times it by the divisor (1 0 1)
1 1 0 0

39. Binary Division
1 0 1 0 1
1 1 0
1 0 1
A subtraction should take place, however you
cannot subtract in binary. Therefore, the two’s
complement of the 2nd number must be found and
the two numbers added together to get a result.
Step 9: The multiplication of the divisor should be
placed under the THREE bits you have used.
0 0 1

40. Binary Division
0 1
1 1 0
0 1 1
0 0 1
Step 10: The two’s complement of 1 0 1 is 0 1 1
0 0 1
1 0 1
+

41. Binary Division
0 1
1 1 0
0 1 1
0 0 1 0
Step 11: Determine if 1 0 1 will fit into the remainder
0 0 1. The answer is no so you must bring down the
next number.
0 0 1
1 0 1
+

42. Binary Division
0 1
1 1 0
0 1 1
0 0 1 0 1
1 0 1
+
Step 12: 1 01 does not fit into 0 0 1 0. Therefore, a
zero is placed above the last bit. And the next number
is used.
0 0 1 0

43. Binary Division
0 1
1 1 0
0 1 1
0 0 0
1 0 1
+
0 0 1 0 1
+
0 1 1
Step 13: 1 0 1 does fit into 1 0 1 so therefore, a one is
placed above the final number and the process of shift
and add must be continued.
0 0 1 0 1

44. Binary Division
Step 14: The final answer is 1 0 1 (5) remainder zero.

45. Activity
4
 Complete the following divisions:
 340 / 20
 580 / 17

46. Activity
5
 40/4
 36/7

57. Subtraction using 1’s And 2’s
Complement

64. Subtraction by 2’s Complement
• The operation is carried out by means of the following
steps:
• At first, 2’s complement of the subtrahend is found.
• Then it is added to the minuend.
• If the final carry over of the sum is 1, it is dropped and
the result is positive.
• If there is no carry over, the two’s complement of the
sum will be the result and it is negative.

69. Octal Arithmetic
• Octal rules are similar to the decimal or binary arithmetic.
• This number system is normally used to enter long strings of
binary data into a digital system like a microcomputer.
• This makes the task of entering binary data in a
microcomputer easier.
• Arithmetic operations can be performed by converting the
octal numbers to binary numbers and then using the rules of
binary arithmetic.

70. Octal Addition

71. Octal Subtraction

72. Application of Octal Number System

73. Hexadecimal Arithmetic
• Hexadecimal rules are similar to the decimal,
octal or binary arithmetic.
• The information can be handled only in binary
form in a digital circuit and it Is easier to enter the
information using hexadecimal number system.
• Arithmetic operations can be performed by
converting the Hexadecimal numbers to binary
numbers and then using the rules of binary
arithmetic.

74. Hexadecimal Addition

75. Hexadecimal Subtraction

78. BCD Addition

79. BCD Subtraction
• Rules
– If EAC(end around carry)=1 then transfer true result of
adder 1
• If Cn=1, 0000 added in adder 2
• If cn =0, 1010 added in adder 2
– If EAC=0 then transfer 1’s compliment of result of adder
1
• If cn=1, 1010 added in adder 2
• If cn =0, 0000 added in adder 2
• If any carry generated in adder 2 discard it.

80. BCD Subtraction
Adder 2

81. BCD Subtraction
• (546) – (429) = (117)
• (429) – (546) = (-117)

82. Excess3 Addition Rules
Step 1
– Convert the numbers into excess 3 forms by adding 0011
Step 2
– Two numbers are added using the basic laws of binary addition
Step 3
– Now which of the four groups have produced a carry we have to
add 0011 with them and subtract 0011 from the groups which
have not produced a carry during the addition.
Step 4
– The result which we have obtained after this operation is in
Excess 3 form and this is our desired result

83. Excess 3 addition

84. Excess 3 Code Subtraction
• Step 1
Like the previous method both the numbers have to be converted
into excess 3 code
• Step 2
Following the basic methods of binary subtraction, subtraction is
done
• Step 3
Subtract ‘0011’ from each BCD four-bit group in the answer if the
subtraction operation of the relevant four-bit groups required a
borrow from the next higher adjacent four-bit group
• Step 4
Add ‘0011’ to the remaining four-bit groups, if any, in the result.

85. Excess 3 Subtraction